普瑞格尔河从古堡哥尼斯堡市中心流过，河中有小岛两座，筑有7座古桥，哥尼斯堡人杰地灵，市民普遍爱好数学。1736年，该市一名市民向大数学家Euler提出如下的所谓“七桥问题”：

从家里出发，7座桥每桥恰通过一次，再回到家里，是否可能？

事实上，人们此前已经反复试验多次，不管怎样游行，亦未成功地实现美桥恰过一次的旅行。但又无人严格证明七桥问题的答案是否定的。

欧拉首先想到的是用穷举法， 就是把所有的走法都一一列出来，然后再一个一个的验证是否可行。 但是他马上发现这样做太麻烦了， 因为对七座桥的不同走法就有7!=5040种，逐一检验太耗时费力了，况且这样的方法没有通用性。如果桥的位置或桥的数量发生变化，岂不又得重新检验? 看来此法不可行。

Euler把两岸分别用C和D两个点来表示，两岛分别用A与B两点来表示。A、B、C、D各点的位置无关紧要，仅当两块陆地之间有桥时，在上述相应的两个点间连有一段曲线段，此曲线段的曲直长短也无关紧要，于是得到图：

欧拉在这里是把实际问题抽象成纯数学模型来进行研究从而获得了解决一类问题的方法。所谓抽象就是把研究的事物从某种角度看待的本质属性抽取出来 进行考察的思维方法。在数学中，例如在由“一个人”“一头羊”“一只猴”或者一个其他什么具体事物抽象出相应的数学概念“1”时，我们所注意的只是这些对象在数量上的共同特征，即量的多少，而根本不去考虑所说对象的质的内容(是人是羊是猴还是别的什么东西)。又如哥尼斯堡七桥问题中，一笔画问题便是从七桥问题中抽象出来的数学模型。在该模型里仅仅保留了一次过七桥的基本属性而舍弃了其他一切属性。

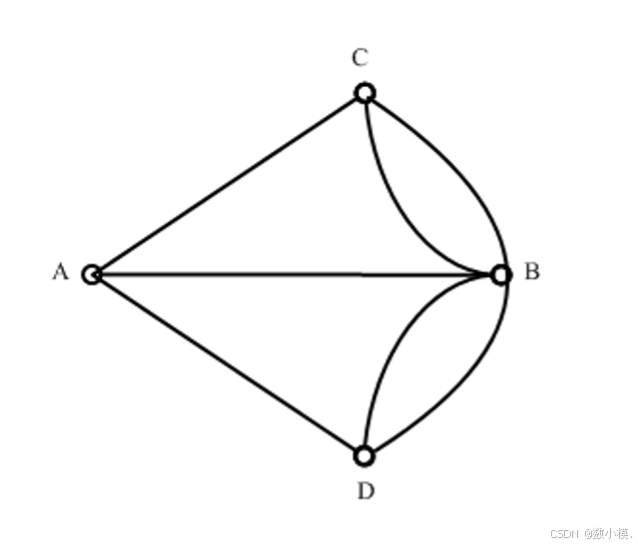
通过数学建模，已经把实际问题转化成了数学问题。这时欧拉注意到，如果一个图形能一笔画成，那么除去起点和终点外，其他的点都是经过点。而经过点是有进有出的点，即有一条线进这个点，就一定有一条线出这个点。不可能有进无出，如果有进无出，它就是终点; 也不可能有出无进，如果有出无进，它就是起点。因此，在经过点进出的线总数应该是偶数。我们称在一个点进出线的总数是偶数的点为偶点; 总数为奇数的点称为奇点。如果起点和终点是同一个点，那么它也属于有进有出的点，它也是偶点，这样图上的点全是偶点。如果起点和终点不是同一个点，那么它们必定是奇点。 因此，能够一笔画的图形最多只有两个奇点。

1736年，欧拉证明了自己的猜想，一次不重复走完七座桥是根本不可能的。随即他发表了“一笔画定理”：

一个图形要能一笔画完，必须符合以下两个条件: 

(1)图形是封闭连通的；

(2)图形中的奇点个数为 0 或 2；

七桥问题中的四个点全是奇点，当然不能一笔画，即不可能一次无重复地走完七座桥。 一般地说，如果图中的点全是偶点，那么可以任意选择一个点作为起点，当然终点与起点重合，能一笔画成；如果图中有两个奇点，那么可以任意选一个奇点作为起点，另一个奇点为终点，可以一笔画成。

欧拉的这个研究成果，开创了图论和拓扑学这两门新的学科。这两门学科在计算机科学中有着广泛的应用。由此可见，只要善于用数学的眼光、数学的方法去观察事物，分析问题，就能把生活中的一些实际问题转化为数学问题，并用数学的方法来处理和解决。