48.路径总和 III(学习)

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例 1：

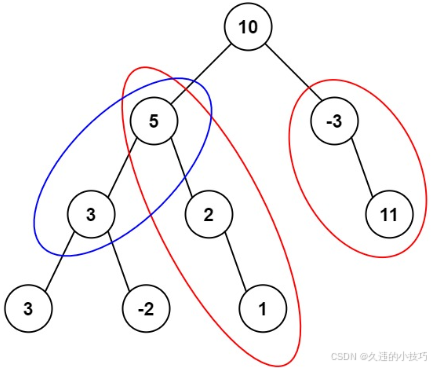
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。

示例 2：
输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：3

提示:
二叉树的节点个数的范围是 [0,1000]
-109 <= Node.val <= 109
-1000 <= targetSum <= 1000

解析：
一、pathSum函数：
1.这是主函数，接收根节点和目标和作为参数，并返回满足条件的路径数量。
2.初始化一个计数器count为0，用于记录满足条件的路径数量。
3.初始化一个Map对象prefixSums，用于存储从根节点到当前节点的路径和及其出现次数。初始时，将路径和为0的情况（表示空路径）的计4.数设为1。

二、DFS函数：
1.这是一个递归函数，用于深度优先搜索树。
2.参数node表示当前访问的节点，currentSum表示从根节点到当前节点的路径和（初始时为0）。
3.更新currentSum以包含当前节点的值。
4.检查是否存在之前的路径和，使得两者之差等于目标和。如果存在，则增加计数器count的值。
5.更新prefixSums中currentSum的计数（如果currentSum已经存在，则增加其计数；否则，将其添加到prefixSums中）。
6.递归地对左子树和右子树执行DFS。
7.注意：虽然代码中包含了回溯部分（即减少当前路径和的计数并从prefixSums中删除它），但在本问题中，由于树是无环的，并且我们不需要精确跟踪每条路径，因此这部分是多余的。在DFS结束后，prefixSums中的条目将自动表示所有可能的路径和及其出现次数。

三、从根节点开始DFS：
1.调用dfs(root, 0)从根节点开始搜索。

四、返回结果：
1.函数返回计数器count的值，即满足条件的路径数量。

var pathSum = function (root, targetSum) {
    let count = 0;
    const prefixSums = new Map(); // 存储从根到当前节点的路径和及其出现次数  
    prefixSums.set(0, 1); // 初始化，表示空路径和为0的情况有1种  

    // 深度优先搜索函数  
    function dfs(node, currentSum) {
        if (!node) return;

        // 更新当前路径和  
        currentSum += node.val;

        // 检查是否存在之前的路径和，使得两者之差等于目标值  
        if (prefixSums.has(currentSum - targetSum)) {
            count += prefixSums.get(currentSum - targetSum);
        }

        // 更新当前路径和的出现次数  
        prefixSums.set(currentSum, (prefixSums.get(currentSum) || 0) + 1);

        // 递归遍历左子树和右子树  
        dfs(node.left, currentSum);
        dfs(node.right, currentSum);

        // 回溯时，需要减去当前节点对路径和的贡献（可选，因为Map会自动处理重复键值）  
        // 但为了保持代码的清晰性和完整性，这里还是显式地处理一下  
        prefixSums.set(currentSum, prefixSums.get(currentSum) - 1);
        if (prefixSums.get(currentSum) === 0) {
            prefixSums.delete(currentSum);
        }
    }

    // 从根节点开始DFS  
    dfs(root, 0);

    return count;
};