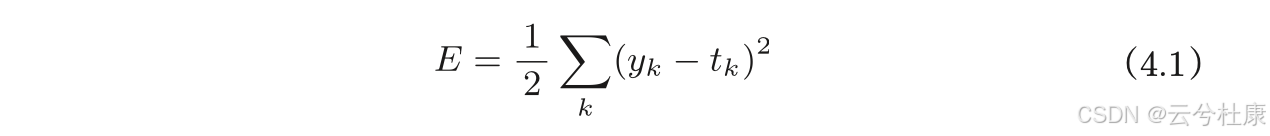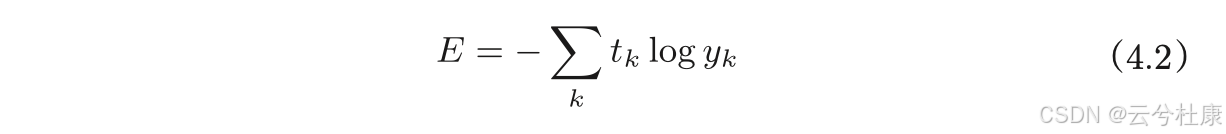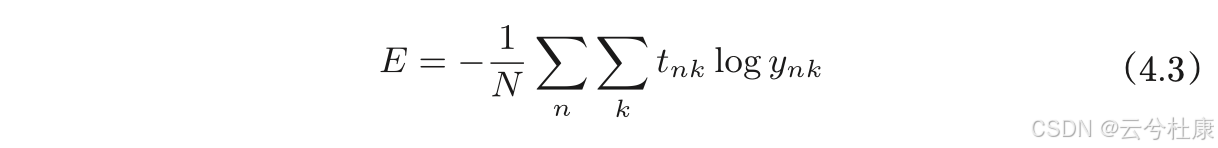4.1.从数据中学习
实际的神经网络中,参数的数量成千上万,因此,需要由数据自动决定权重参数的值。
4.1.1.数据驱动
数据是机器学习的核心。
我们的目标是要提取出特征量,特征量指的是从输入数据/图像中提取出的本质的数 据,特征量通常表示为向量的形式。
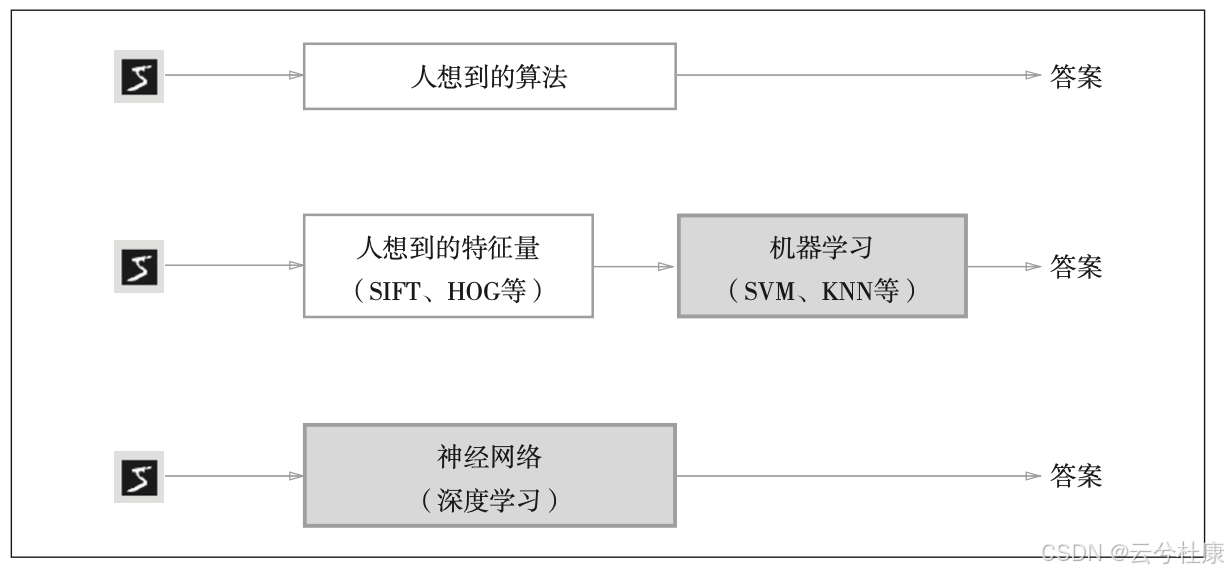
有两种方法:a. 使用人想到的特征量将图像数据转换为向量,然后对转换后的向量使用机器学习中的SVM、KNN等分类器进行学习【关于这一点,我的想法是,如果使用传统算法来提取特征,就根据经验针对不同的问题选取合适的特征量】;b.直接使用神经网络来实现端到端【从原始数据直接获得输出结果】的学习。 这两个方法目的一样,都是为了从原始数据中提取出本质的数据或信息。
4.1.2.训练数据和测试数据
获得泛化能力是机器学习的最终目标。
仅仅用一个数据集去学习和评价参数,是不客观的,可能会导致可以顺利地处理某个数据集,但无法处理其他数据集的情况,即过拟合。
为了避免过拟合,追求模型的泛化能力【指处理未被观察过的数据】【举例来说,识别手写数字的问题,泛化能力可能会被用在自动读取明信片的邮政编码的系统上,此时,手写识别的就是“任何一个人写的任意文字”,而不是“特定某个人写的特定的文字”】,需要划分训练集和测试集。使用训练数据进行学习,寻找最优的参数,然后,利用测试数据评价训练得到的模型的实际能力。
4.2.损失函数
神经网络的学习中使用损失函数来寻找最优权重参数,这里的损失函数可以用任意函数,一般用均方误差和交叉熵误差。
4.2.1.均方误差
【one-hot表示:正确解标签表示为1,其他标签表示为0】
def mean_squared_error(y, t):
return 0.5 * np.sum((y-t)**2)4.2.2.交叉熵误差
这里的tk是正确解标签,并且,只有正确解标签的索引为1,其他的索引均为0(one-hot表示),因此,式子4.2实际上只计算对应正确解标签的输出的自然对数。
def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y + delta))这里在log里加了一个很小的delta的值,为了防止y为0时,log值为-inf,这样会导致后续计算无法进行,即相当于一个保护性对策。
4.2.3.mini-batch学习
MNIST 数据集的训练数据有 60000 个,一些大的数据,数据量页会有几百万、几千万之多,这种情况下以全部数据为对象计算平均损失函数是不现实的。因此,从全部数据中选出一部分,作为全部数据的“近似”。神经网络的学习也是从训练数据中选出一批数据,然后对每个mini-batch进行学习。这种学习方式称为mini-batch学习。
以交叉熵误差为例,求所有训练数据的损失函数的总和,把单个数据的“平均损失函数”的式扩大到了N份数据,最后除以N进行正规化,即得出单个数据的“平均损失函数”:【通过这样的平均化,可以获得和训练数据的数量无关的统一指标】
举例介绍一下mini-batch学习的编码过程:
a.读入 MNIST 数据集
import sys, os sys.path.append(os.pardir)
import numpy as np
from dataset.mnist import load_mnist
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
print(x_train.shape) # (60000, 784) print(t_train.shape) # (60000, 10)one_hot_label设置为True,表示正确解标签为1,其余为0。
b.从训练数据中随机选取10笔数据
使用NumPy的np.random.choice(),可以从指定的数字中随机选取想要的数字,即
train_size = x_train.shape[0]
batch_size = 10
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]之后,指定这些随机选取的索引,取出mini-batch,然后使用mini-batch计算损失函数即可。
4.2.4.mini-batch版交叉熵误差的实现
当监督数据t是one-hot形式时,可实现一个同时处理单个数据和批量数据batch两种情况的函数:
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size当监督数据t是标签形式时(非 one-hot 表示,而是像“2”“7”这样的 标签),可通过如下代码实现:
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size介绍一下代码实现中的np.log(y[np.arange(batch_size), t] + 1e-7):np.arange(batch_size)会生成一个从0到batch_size-1的数组。例如当batch_size为5时,np.arange(batch_size)会生成一个NumPy数组[0,1,2,3,4]。由于t中标签是以[2,7,0,9,4]的形式存储的,所以y[np.arange(batch_size), t]能抽出各个数据的正确解标签对应的神经网络的输出(在这个例子中,y[np.arange(batch_size), t]会生成NumPy数组[y[0,2], y[1,7], y[2,0], y[3,9], y[4,4]]。
4.2.5.为什么要设定损失函数
以数字识别任务为例,目的既然是能提高识别精度的参数,那特意导入一个损失函数不是有些重复劳动吗?为什么不直接把识别精度作为指标?
对于这个疑问,我们来关注一下神经网络的某一个权重参数,对该权重参数的损失函数求导,如果导数值为正,则该权重参数向负方向改变可减小损失函数的值,反之,权重参数向正方向改变可减小损失函数的值。若导数为0,则无论权重参数向哪个方向变化,损失函数的值都不会变,即权重参数的更新会停留在此处。【而之所以不用识别精度作为指标,是因为绝大多数地方的导数都会变为0,导致参数无法更新,而且识别精度的值也不像损失函数作为指标时那样连续变化,即识别精度对微小的参数变化基本上没有什么反应】