DP35 【模板】二维前缀和
解法一:暴力解法 -> 模拟
直接算区间里面的和
每次询问都要遍历数组一遍
时间复杂度:O(n*m*q)
解法二:前缀和
1. 预处理出来一个前缀和矩阵
dp[i][j]表示:从[1,1]位置到[i,j]位置,这段区间里面所有元素的和
dp[i][j] = A + B + C + D = (A + B) + (A + C) + D - A
A + B = dp[i-1][j]
A + C = dp[i][j-1]
D = arr[i][j]
A = dp[i-1][j-1]
直接遍历dp一遍就能全部得出来
2. 使用前缀和矩阵
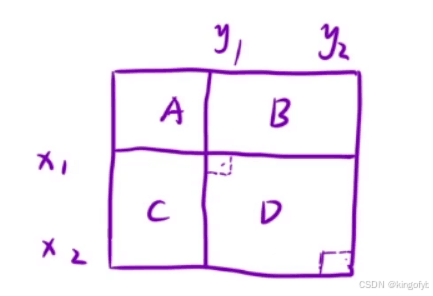
求的是[x1,y1] ~ [x2,y2]
先算出整个区域的面积,再减去
D = A + B + C + D - (A+B) - (A+C) + A
A + B + C + D = dp[x2][y2]
A + B = dp[x1-1][y2]
A + C = dp[x2][y1-1]
A = dp[x1-1][y1-1]
A区域
B,C
使用
时间复杂度:O(m*n) + O(q)
代码:C++
#include <iostream>
#include <vector>
using namespace std;
int main()
{
// 1. 读入数据
int n = 0, m = 0, q = 0;
cin >> n >> m >> q;
// 因为下标是从1开始计数的,所以m和n要+1才能访问到[m][n]这个位置
vector<vector<int>> arr(n+1, vector<int>(m+1));
for(int i=1; i<=n; i++)
{
for(int j=1; j<= m; j++)
{
cin >> arr[i][j];
}
}
// 2. 预处理前缀和矩阵,longlong防止溢出
vector<vector<long long>> dp(n+1, vector<long long>(m+1));
for(int i=1; i<=n; i++)
{
for(int j=1; j<= m; j++)
{
dp[i][j] = dp[i-1][j] + dp[i][j-1] + arr[i][j] - dp[i-1][j-1];
}
}
// 3. 使用前缀和矩阵,一共q次,所以q--
int x1=0, y1=0, x2=0, y2=0;
while(q--)
{
cin >> x1 >> y1 >> x2 >> y2;
cout << dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1] << endl;
}
return 0;
}13. 罗马数字转整数
可以直接创建一个罗马数字的映射表然后判断情况。如果当前字符不是最后一个字符并且当前字符的数值小于下一个字符的数值,就减去当前字符,可以参考IV = 4
代码:C++
class Solution {
public:
int romanToInt(string s)
{
// 建立罗马数字到整数的映射
unordered_map<char, int> roman_map = {
{'I', 1},
{'V', 5},
{'X', 10},
{'L', 50},
{'C', 100},
{'D', 500},
{'M', 1000}
};
int result = 0;
int n = s.size();
for(int i=0; i<n; i++)
{
// 如果当前字符不是最后一个字符,并且当前字符表示的数值小于下一个字符表示的数值
if(i < n-1 && roman_map[s[i]] < roman_map[s[i+1]])
{
// 减去当前字符表示的数值
result -= roman_map[s[i]];
}
else
{
result += roman_map[s[i]];
}
}
return result;
}
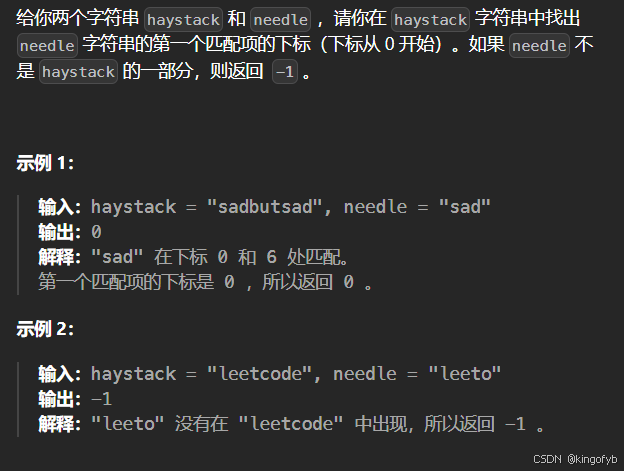
};28. 找出字符串中第一个匹配项的下标
28. 找出字符串中第一个匹配项的下标 - 力扣(LeetCode)
解法一:KMP算法
构建部分匹配表并记录needle中每个位置的最长相同前缀后缀的长度。
然后匹配haystack和needle,如果不匹配可以根据部分匹配表数组直接跳到可能的匹配位置,而不必从头重新匹配。
解法二:暴力匹配
代码:C++
class Solution {
public:
int strStr(string haystack, string needle)
{
int n = haystack.size(), m = needle.size();
// 外循环遍历 haystack 的每一个可能的起始位置 i(范围为 0 到 n - m)。
for(int i=0; i+m <= n; i++)
{
bool flag = true;
// 内循环遍历 needle 的每一个字符,检查 haystack 从 i 位置开始的子串是否与 needle 匹配。
for(int j=0; j<m; j++)
{
if(haystack[i+j]!=needle[j])
{
flag = false;
break;
}
}
// 如果发现匹配子串,返回其起始位置 i
if(flag)
{
return i;
}
}
return -1;
}
};66. 加一
-
从数组的末尾开始处理:
- 从最低位(数组最后一位)开始向前遍历。
- 如果当前位的数字小于 9,则加 1,并直接返回结果,因为加 1 不会产生进位。
- 如果当前位的数字是 9,将其置为 0,然后继续向前处理,因为需要向更高位进 1。
-
处理进位:
- 如果数组中的所有元素都是 9,则遍历结束后,所有位都将变成 0。
- 这种情况下,需要在数组的开头插入一个 1,表示最高位的进位。
代码:C++
class Solution {
public:
vector<int> plusOne(vector<int>& digits) {
int n = digits.size(); // 获取数组的长度
// 从数组的最后一个元素开始遍历
for (int i = n - 1; i >= 0; --i) {
if (digits[i] < 9) { // 如果当前元素小于9
digits[i] += 1; // 将当前元素加一
return digits; // 直接返回结果
}
digits[i] = 0; // 如果当前元素等于9,将其置为0
}
// 如果所有元素都是9,则在数组的开头插入1
digits.insert(digits.begin(), 1);
return digits; // 返回结果
}
};