先赞美一下拉格朗日,在学习了中值定理之后,又来挑战插值法了。
拉格朗日插值法有个致命缺点,太轴了,过分追求完美一个数据也不放过,当数据出现异常值时,最终拟合的多项式并不会剔除它们。
数学公式:
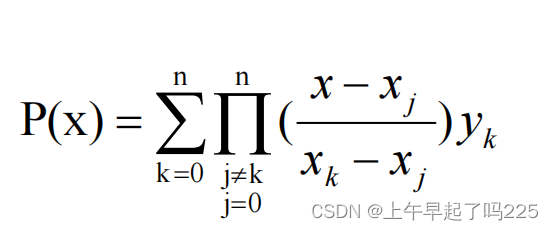
python的 scipy.interpolate . lagrange将其实现。
1. 对dataframe缺失值进行插值代码实现(已解决小坑代码)
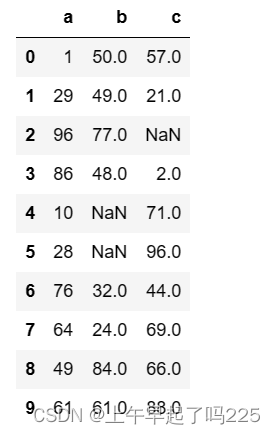
先生成含缺失值的dataframe:
import numpy as np
import pandas as pd
df=pd.DataFrame(np.random.randint(1,100,size=(50,3)),columns=['a','b','c'])
df
df.iloc[2,2]=None
df.iloc[4:6,1]=None
df.head(10)
插值实现:
data表示插值的某列数据
k表示要拟合的邻近个数 ,前k个和后k个
from scipy.interpolate import lagrange
def chazhi(data,k):
n_index=data[data.isnull()].index
for n in n_index:
# print(n)
y=data.iloc[list(range(n-k,n))+list(range(n+1,n+1+k))]
y=y[y.notnull()]
data[n]=lagrange(y.index,list(y))(n)
print(data[n])
return data
# dt=df['c']
# # print(dt)
# chazhi(dt,2)
# print(df)
# # print(df1)
df2=df.copy()
for i in df.columns:
# print(i)
dt=df[i].copy()
df2[i]=chazhi(dt,2)
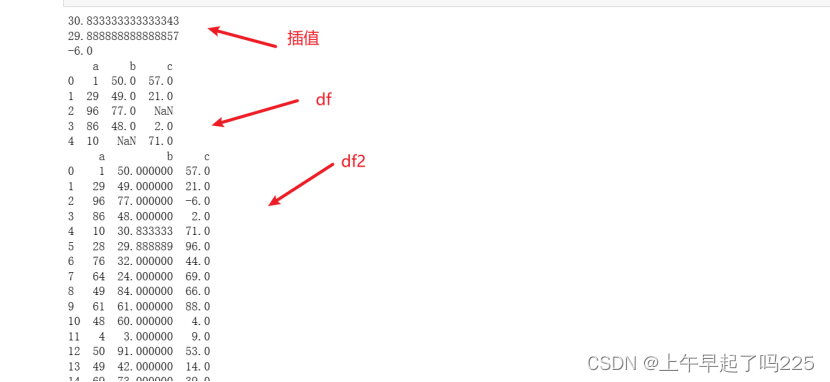
print(df.head())
print(df2)
print('ok')
2.小坑
想保留未插值前的数据却无法实现
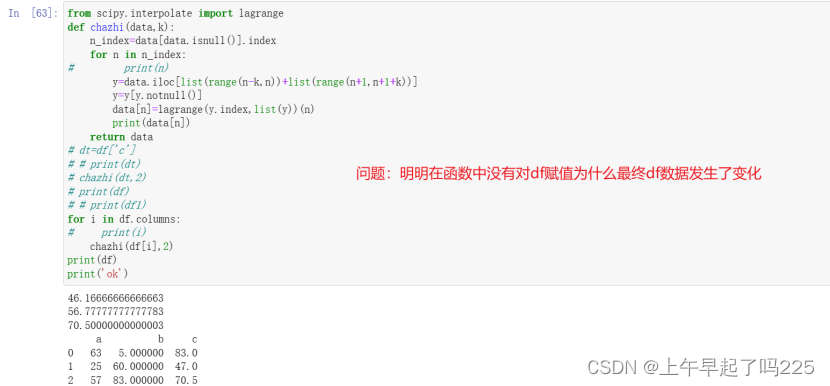
就像是指针的问题,其实并没有给dt分配空间,在函数内更改的空间位置是原df