一、排序算法
1、插入排序
1.1 直接插入排序
void InsertSort(int A[], int n) {
int temp, i, j; // 定义三个变量,temp用于存储需要插入的元素,i用于外层循环,j用于内层循环
for (i = 1; i < n; i++) { // 外循环,从第二个元素开始,每个元素都要进行排序
if (A[i - 1] > A[i]) { // 如果当前元素前面的元素比当前元素大,则需要进行排序
temp = A[i]; // 将当前元素保存到temp中
for (j = i - 1; A[j] > temp && j >= 0; j--) { // 内层循环,从当前元素的前一个元素开始,向前比较
A[j + 1] = A[j]; // 将比temp大的元素向后移动一位
}
// 该趟排序结束,找到temp应该插入的位置
A[j + 1] = temp; // 将temp插入到正确的位置
}
}
}1.2、折半查找排序(直接插入算法的改进)
void sort(int A[], int n) {
int mid, temp, j;
for (int i = 1; i < n; i++) {
temp = A[i];
int low = 0;
int high = i - 1; // 注意是 i-1
while (low <= high) { // 注意是 <=保证稳定性
mid = (low + high) / 2;
if (A[mid] > temp) { //表示插入元素在左边
high = mid - 1;
} else {
low = mid + 1;
}
}
//将low到i-1的元素全部右移
for (j = i - 1; j >= low; j--) {
A[j + 1] = A[j];
}
A[low] = temp;
}
}
1.3、希尔排序
void ShellSort(int A[], int n) {
int i,temp,j,d;
for(d = n/2;d>=1;d = d/2){ //每次循环的增量
for(i=d;i<n;i++){ //每组循环
temp = A[i];
for(j = i;j>=d && A[j-d] > temp;j-=d){
A[j] = A[j-d];
}
A[j] = temp;
}
}
}2、交换排序
2.1 冒泡排序
void Swap(int &a, int &b) {
int temp = a;
a = b;
b = temp;
}
void BubbleSort(int A[], int n) {
int i ,j;
bool flag;
for( i = n-1;i>=0;i--){
flag = false;
for(j = 0;j<i;j++){
if(A[j] < A[j+1]){ //冒小泡 >就是冒大泡,大的在后面
Swap(A[j],A[j+1]);
flag = true;
}
}
if(flag == false){
break;
}
}
}
2.2 快速排序
// 快速排序中的划分函数
// A[] 是待排序数组,low 是数组的起始索引,high 是数组的结束索引
int Partition(int A[], int low, int high) {
// 选择数组的第一个元素作为基准元素
int pivot = A[low];
// 从数组的起始索引开始,向 high 移动
while (low < high) {
// 从数组的结束索引开始,向 low 移动,直到找到一个小于基准的元素
while (low < high && A[high] >= pivot) {
high--;
}
// 将找到的小于基准的元素放到 low 的位置
A[low] = A[high];
// 从数组的起始索引开始,向 high 移动,直到找到一个大于基准的元素
while (low < high && A[low] <= pivot) {
low++;
}
// 将找到的大于基准的元素放到 high 的位置
A[high] = A[low];
}
// 将基准元素放到最终的位置
A[low] = pivot;
// 返回基准元素的索引
return low;
}
// 快速排序函数
// A[] 是待排序数组,low 是数组的起始索引,high 是数组的结束索引
void QuickSort(int A[], int low, int high) {
// 如果 low 小于 high,说明还有元素需要排序
if (low < high) {
// 调用划分函数,得到基准元素的索引
int pivotos = Partition(A, low, high);
// 对基准元素左边的子数组进行快速排序
QuickSort(A, low, pivotos - 1);
// 对基准元素右边的子数组进行快速排序
QuickSort(A, pivotos + 1, high);
}
}3、选择排序
3.1 简单选择排序
// 交换两个整数的值
void Swap(int &a, int &b) {
int temp = a; // 临时变量,用于交换
a = b; // 将b的值赋给a
b = temp; // 将temp(原来的a的值)赋给b
}
// 选择排序函数
void SelectSort(int A[], int n) {
// 遍历数组,直到倒数第二个元素。
for (int i = 0; i < n - 1; i++) {
int min = i; // 记录此轮选择的最小元素的索引
// 遍历当前未排序的部分(即从索引i+1到n-1),寻找最小元素。
for (int j = i + 1; j < n; j++) {
if (A[j] < A[min]) {
min = j; // 更新最小元素的位置
}
}
// 如果找到的最小元素不是当前位置i,那么交换它们。
if (min != i) {
Swap(A[i], A[min]); // 传递数组元素的地址,进行交换
}
}
}3.2 堆排序
// 交换两个整数的值
void swap(int *a, int *b) {
int temp = *a;
*a = *b;
*b = temp;
}
// 调整以k为根节点的树成为大根堆
void HeadJust(int A[], int k, int n) {
int temp = A[k];
// 1.找到该节点的左右孩子中最大的那个
for (int i = 2 * k; i <= n; i *= 2) {
if (i < n && A[i + 1] > A[i]) {
i++; // 如果右孩子存在且比左孩子大,则选择右孩子
}
// 2.找到更大的元素后判断最大位置的元素和k位置上的元素大小
if (temp >= A[i]) {
break; // 如果temp已经大于或等于i位置的元素,则停止调整
} else {
// 3.将该位置的元素赋值到k位置上
A[k] = A[i];
k = i; // 因为i位置上的元素已经保存到k位置上了,因此这里需要将k指向i位置,以该节点为根节点继续调整
}
}
A[k] = temp; // k位置不存在左右孩子,因此将元素放到k位置
}
// 构建大根堆
void build(int A[], int n) {
for (int i = n / 2; i >= 1; i--) { // 从最后一个非叶子节点开始调整
HeadJust(A, i, n); // 调整每个非叶子节点,使其成为大根堆
}
}
// 堆排序
void sort(int A[], int n) {
build(A, n); // 构建大根堆
for (int i = n; i > 1; i--) {
swap(&A[i], &A[1]); // 将堆顶元素(最大值)与数组末尾元素交换
HeadJust(A, 1, i - 1); // 调整堆,使其再次成为大根堆
}
}4、归并排序
int* B = (int *)malloc(10 * sizeof(int)); // 辅助数组B
// 合并两个有序数组的函数
void Merge(int A[], int low, int mid, int high) {
int i, j, k;
// 将A中所有元素复制到B中
for (k = low; k <= high; k++) {
B[k] = A[k];
}
// 使用for循环将较小值复制到A中
for (i = low,j = mid + 1, k = i; i <= mid && j <= high; k++) {
if (B[i] <= B[j]) {
A[k] = B[i++];
} else {
A[k] = B[j++];
}
}
// 复制剩余的元素
while (i <= mid) {
A[k++] = B[i++];
}
while (j <= high) {
A[k++] = B[j++];
}
}
// 归并排序函数
void MergeSort(int A[], int low, int high) {
if (low < high) {
int mid = (low + high) / 2;
// 对左半部分归并排序
MergeSort(A, low, mid);
// 对右半部分归并排序
MergeSort(A, mid + 1, high);
// 归并
Merge(A, low, mid, high);
}
}
5、基数排序(略)
二、查找
1、顺序查找和折半查找
1.1 折半查找
int Binary_Search(int A[], int n, int x) {
int low = 0;
int high = n - 1;
int mid;
while (low <= high) {
mid = (low + high) / 2;
if (A[mid] == x) {
return mid;
} else if (A[mid] > x) {
high = mid - 1;
} else {
low = mid + 1;
}
}
return -1;
}2、树形查找
2.1 二叉排序树(BST)
二叉排序树非递归算法查找
BiTree BST_Search(BiTree T,int key){
while(T != NULL && key != T->data){
if(key < T->data){ //去左子树查找
T = T->lchild;
}else{
T = T->rchild;
}
}
return T;
} 二叉排序树的递归查找
//BST中序遍历是有序的,先序后序都行
BiTree BST_Search(BiTree T,int key){
if(T == NULL){
return NULL;
}
BST_Search(T->lchild,key);
if(T->data == key){
return T;
}
BST_Search(T->rchild,key);
}二叉排序树的递归插入
int BST_Insert(BiTree &T,int key){
if(T == NULL){
T = new BiTNode;
T->data = key;
T->rchild = T->lchild = NULL;
return 1;
}else if(key == T->data){
return 0; //存在相同值的节点插入失败
}else if(key < T->data){
return BST_Insert(T->lchild,key);
} else{
return BST_Insert(T->rchild,key);
}
} 二叉排序树的非递归插入
不想写,暂略。
判断给定的二叉树是不是二叉排序树
int pre = -100; // 全局变量,用作记忆指针,存储前一个访问节点的值
// 判断二叉树是否为二叉排序树的函数
// 参数 T 是二叉树的根节点
int BST_Judge(BiTree T){
int L, R; // 定义两个变量,分别存储左子树和右子树的判断结果
// 如果当前节点为空,返回1,因为空树也是二叉排序树
if(T == NULL){
return 1;
}
// 递归调用BST_Judge函数,判断左子树是否为二叉排序树,并将结果存储在L中
L = BST_Judge(T->lchild);
// 如果左子树不是二叉排序树(L为0),或者当前节点的值小于前一个节点的值(pre),则返回0
if(L == 0 || T->data < pre){
return 0;
}
// 将当前节点的值赋给pre,作为下一个节点的前驱节点值
pre = T->data;
// 递归调用BST_Judge函数,判断右子树是否为二叉排序树,并将结果存储在R中
R = BST_Judge(T->rchild);
// 返回右子树的判断结果R
return R;
}如果不好想的话,可以中序遍历放到数组中,然后挨个比较。
int data[100] = {0}; // 假设数组足够大
int index = 0;
void Mid(BiTree T) {
if (T == NULL) {
return; // 空树也是二叉排序树
}
Mid(T->lchild);
data[index++] = T->data;
Mid(T->rchild);
}
bool Judge_BST() {
for (int i = 0; i < index - 1; i++) {
if (data[i] >= data[i + 1]) {
return false; // 不是二叉排序树
}
}
return true; // 是二叉排序树
}求出指定节点在二叉树的层次
实际上就是求某个节点在二叉树的层次。
int getLevel(BiTree T, int k, int level) {
// 如果当前节点为空,返回0,表示没有找到值为k的节点
if (T == NULL) {
return 0;
}
// 递归地在左子树中查找值为k的节点,并将层数增加1
getLevel(T->lchild, k, level++);
// 如果当前节点的值等于k,返回当前的层数
if (T->data == k) {
return level;
}
// 如果当前节点的值不等于k,递归地在右子树中查找值为k的节点,并将层数增加1
getLevel(T->rchild, k, level++);
}求二叉排序树中最大值和最小值
//最大值在最右边
ElemType getMax(BiTree T){
if(T->rchild != NULL){
T = T->rchild;
}
return T->data;
}
//最小值在最左边
ElemType getMin(BiTree T){
if(T->lchild != NULL){
T = T->lchild;
}
return T->data;
}想不到的话还能用数组。
// 中序遍历二叉树,并将元素存储到数组中
ElemType data[100] = {0};
int index = -1;
void Mid(BiTree T) {
if (T == NULL) {
return;
} else {
Mid(T->lchild);
data[++index] = T->data;
Mid(T->rchild);
}
}
void getMaxAndMin(){
cout<<"最小值是:"<<data[0]<<" 最大值是:"<<data[index];
}从大到小输出二叉排序树中值不小于K的元素
// 查找二叉排序树中值不小于K的元素的函数
void search(BiTree T, ElemType e) {
// 如果当前节点为空,返回,不进行任何操作
if (T == NULL) {
return;
}
// 递归地在左子树中搜索,寻找所有不小于e的元素
search(T->rchild, e);
// 如果当前节点的值大于等于e,打印该元素
if (T->data >= e) {
cout << "不小于" << e << "的元素:" << T->data << endl;
}
// 递归地在右子树中搜索,寻找所有不小于e的元素
search(T->lchild, e);
}或者是直接使用数组,中序遍历放到数组中。
2.2 二叉平衡树
判断二叉树是不是二叉平衡树
//求二叉树高度
int getHight(BiTree T){
int hl,hr;
if(T == NULL){
return 0;
}else{
hl = getHight(T->lchild);
hr = getHight(T->rchild);
if(hl > hr){
return hl+1; //1是当前节点本身高度
}else{
return hr+1;
}
}
}
//判断一颗二叉树是否为平衡二叉树
bool isBlance(BiTree T){
int hight_l; //左子树高度
int hight_r; //右子树高度
if(T == NULL){
return true; //空树也是个平衡二叉树
}else{
hight_l = getHight(T->lchild); //求左子树高度
hight_r = getHight(T->rchild); //求右子树高度
if(abs(hight_l-hight_r) <= 1){
return isBlance(T->lchild) && isBlance(T->rchild);
}else{ //根节点不是二叉树
return false;
}
}
}三、图
邻接矩阵的结构体
// 邻接矩阵结构体
typedef struct Graph {
ElemType maxvexs[100]; // 顶点,最多100个
int maxarcs[100][100]; // 边
int vexsnum; // 顶点数
int arcsnum; // 边数
int kind; // 图的类型 1表示该图是无向图,0表示是有向图
} Graph;1.1 邻接矩阵
邻接矩阵的BFS
下面的BFS算法都适用于有向图和无向图的邻接矩阵
// 寻找顶点v的第一个邻居顶点
int firstNeighbor(Graph G, int v) {
for (int i = 0; i < G.vexsnum; i++) { // 遍历所有顶点
if (G.arcs[v][i] != maxweight) { // 如果v到i的边不是最大权重(即存在边)
return i; // 返回第一个邻居的索引
}
}
return -1; // 如果没有邻居,则返回-1
}
// 寻找顶点v1除了v2之外的下一个邻居顶点
int nextNeighbor(Graph G, int v1, int v2) {
for (int i = v2 + 1; i < G.vexsnum; i++) { // 从v2的下一个顶点开始遍历
if (G.arcs[v1][i] != maxweight) { // 如果v1到i的边不是最大权重(即存在边)
return i; // 返回下一个邻居的索引
}
}
return -1; // 如果没有其他邻居,则返回-1
}
// 访问标记数组,用于记录顶点是否被访问过
bool visited[100];
// 广度优先遍历算法
void BFS(Graph G, int v) {
visit(G.vexs[v]); // 访问顶点v
visited[v] = true; // 标记顶点v为已访问
Queue Q; // 创建队列Q
initQueue(Q); // 初始化队列Q
push(Q, v); // 将顶点v入队
while (Q.front != Q.rear) { // 当队列不为空时
int u;
pop(Q, u); // 出队一个顶点u
for (int w = firstNeighbor(G, u); w >= 0; w = nextNeighbor(G, u, w)) { // 找到u的所有邻居
if (!visited[w]) { // 如果邻居w未被访问
visited[w] = true; // 标记邻居w为已访问
visit(G.vexs[w]); // 访问邻居w
push(Q, w); // 将邻居w入队
}
}
}
}
// 广度优先遍历所有连通分量
void BFSTraverse(Graph G){
for(int i = 0; i < G.vexsnum; ++i){
visited[i] = false; // 初始化访问标记数组
}
for(int i = 0; i < G.vexsnum; ++i){
if(!visited[i]){ // 如果顶点i未被访问
BFS(G, i); // 对顶点i进行广度优先遍历
}
}
}邻接矩阵的DFS
同样下面的DFS算法都适用于有向图和无向图的邻接矩阵。
// 找某个顶点的第一个邻居
int firstNeighbor(Graph G, int v) {
for (int i = 0; i < G.vexsnum; i++) {
if (G.arcs[v][i] != maxweight) {
return i;
}
}
return -1; // 没有邻居时返回-1
}
// 找到v1顶点除了邻居v2的其他邻居,返回的是第一个邻居的下标
int nextNeighbor(Graph G, int v1, int v2) {
for (int i = v2 + 1; i < G.vexsnum; i++) {
if (G.arcs[v1][i] != maxweight) {
return i;
}
}
return -1; // 没有其他邻居时返回-1
}
//访问标记数组
bool visited[100];
// 深度优先遍历算法
void DFS(Graph G, int v) {
visited[v] = true;
visit(G.vexs[v]);
for (int w = firstNeighbor(G, v); w != -1; w = nextNeighbor(G, v, w)) {
if (!visited[w]) {
DFS(G, w);
}
}
}
// 深度优先遍历所有连通分量
void DFSTraverse(Graph G){
for(int i = 0; i < G.vexsnum; i++){
visited[i] = false;
}
for(int i = 0; i < G.vexsnum; ++i){
if(!visited[i]){
DFS(G, i); // 传递顶点的索引
}
}
}1.2 邻接表
邻接表的结构体
// 边节点的结构体
typedef struct ArcNode {
int index; // 节点的索引
struct ArcNode* nextArc; // 指向下一个边节点的指针
} ArcNode;
// 顶点节点的结构体
typedef struct VNode {
ElemType data; // 顶点的数据
ArcNode* firstArc; // 指向第一个边节点的指针
} VNode, AdjList[max];
// 图的结构体
typedef struct Graph {
AdjList vertice; // 顶点数组
int vexnum; // 顶点数
int arcnum; // 边数
int kind; // 图的类型
} Graph;邻接表的BFS
// 找到某个顶点的第一个邻居
int firstNeighbor(Graph G, int v) {
ArcNode *p = G.vertices[v].firstarc; // 获取顶点v的邻接链表的第一个节点
if (p) return p->index; // 如果存在邻居,返回第一个邻居的索引
return -1; // 如果没有邻居,返回-1
}
// 找到v1顶点除了邻居v2的其他邻居,返回的是第一个邻居的下标
int nextNeighbor(Graph G, int v, int v2) {
ArcNode *p = G.vertices[v].firstarc; // 获取顶点v的邻接链表的第一个节点
while (p) { // 遍历邻接链表
if (p->index != v2) return p->index; // 如果找到不是v2的邻居,返回其索引
p = p->nextarc; // 移动到下一个节点
}
return -1; // 如果没有其他邻居,返回-1
}
// 广度优先遍历算法
void BFS(Graph G, int v) {
visit(G.vertices[v].data); // 访问顶点v
visited[v] = true; // 标记顶点v为已访问
Queue Q; // 创建队列Q
initQueue(Q); // 初始化队列Q
push(Q, v); // 将顶点v入队
while (Q.front != Q.rear) { // 当队列不为空时
int u; // 临时变量,用于存储出队的顶点索引
pop(Q, u); // 从队列中出队一个顶点
for (int w = firstNeighbor(G, u); w >= 0; w = nextNeighbor(G, u, w)) { // 对于顶点u的每个邻居w
if (!visited[w]) { // 如果邻居w未被访问
visited[w] = true; // 标记邻居w为已访问
visit(G.vertices[w].data); // 访问邻居w
push(Q, w); // 将邻居w入队
}
}
}
}邻接表的DFS
// 找到某个顶点的第一个邻居
int firstNeighbor(Graph G, int v) {
ArcNode *p = G.vertices[v].firstarc;
if (p) return p->index;
return -1; // 没有邻居时返回-1
}
// 找到v1顶点除了邻居v2的其他邻居,返回的是第一个邻居的下标
int nextNeighbor(Graph G, int v, int v2) {
ArcNode *p = G.vertices[v].firstarc;
while (p) {
if (p->index!= v2) return p->index;
p = p->nextarc;
}
return -1; // 没有其他邻居时返回-1
}
void DFS(Graph G, int v) {
visited[v] = true;
visit(G.vertices[v].data);
for (int w = firstNeighbor(G, v); w >= 0; w = nextNeighbor(G, v, w)) {
if (!visited[w]) {
DFS(G, w);
}
}
}不管是邻接表还是邻接矩阵在实现上都差不多主要是firstNeibor和nextNeibor有点不同。
1.3 习题
判断一个无向图是不是一颗树(邻接表)
条件:无回路连通图或n-1边的连通图
// 访问标记数组,用于记录顶点是否被访问过
bool visited[max] = {false}; // 访问标记数组,max 应替换为实际的最大顶点数
// 深度优先遍历(DFS)算法
void DFS(Graph &G, int v, int &vexnum, int &arcnum) {
visited[v] = true; // 标记当前顶点v为已访问
vexnum++; // 访问的顶点数量加1
for (ArcNode* p = G.vertice[v].firstArc; p != NULL; p = p->nextArc) { // 遍历顶点v的所有邻接点
if (!visited[p->index]) { // 如果邻接点p未被访问过
arcnum++; // 访问的边数量加1
DFS(G, p->index, vexnum, arcnum); // 递归访问邻接点p
}
}
}
// 判断图是否是树
bool isTree(Graph &G, int start) {
int vexnum = 0; // 初始化访问的顶点数量
int arcnum = 0; // 初始化访问的边数量
DFS(G, start, vexnum, arcnum); // 从起始顶点开始深度优先遍历
return vexnum == G.vexnum && arcnum == G.vexnum - 1; // 如果访问的顶点数等于图中顶点数,且边数等于顶点数减1,则图是树
}判断一个无向图是不是一颗树(邻接矩阵)
// 访问标记数组,用于记录顶点是否被访问过
bool visited[100];
// 深度优先遍历算法,同时计算边的数量
void DFS(Graph G, int v, int *arcnum) {
visited[v] = true; // 标记当前顶点v为已访问
for (int w = firstNeighbor(G, v); w != -1; w = nextNeighbor(G, v, w)) {
if (!visited[w]) { // 如果邻居w未被访问过
(*arcnum)++; // 边数量加1
DFS(G, w, arcnum); // 递归访问邻居w
}
}
}
// 深度优先遍历所有连通分量,同时检查图是否是树
bool DFSTraverse(Graph G) {
int arcnum = 0; // 初始化边的数量
for (int i = 0; i < G.vexsnum; i++) {
visited[i] = false; // 初始化访问标记数组
}
for (int i = 0; i < G.vexsnum; ++i) {
if (!visited[i]) { // 如果顶点i未被访问过
DFS(G, i, &arcnum); // 从顶点i开始深度优先遍历,并计算边的数量
}
}
// 检查边的数量是否等于顶点数减一,如果是,则图是树
return arcnum == G.vexsnum - 1;
}四、树和二叉树
二叉树的先、中、后代码略。
1 二叉树求高度
// 递归函数,用于计算二叉树的高度
int getHigh(BiTree T) {
if (T == NULL) {
return 0; // 如果当前节点为空,返回高度0
} else {
int lh = getHigh(T->lchild); // 递归计算左子树的高度
int rh = getHigh(T->rchild); // 递归计算右子树的高度
return 1 + (lh > rh ? lh : rh); // 返回1(当前节点)加上左右子树中较高的那个高度
}
}
//求二叉树的高度(非递归)
int getHigh2(BiTree T) {
if (T == NULL) {
return 0; // 如果树为空,返回高度0
}
int h = 0; // 树的高度
// 初始化队列
Queue Q;
Q.front = Q.rear = -1;
int p = 0; // 工作指针指向该层的最后一个节点,front指针和p指针重合的时候树的高度++
enqueue(Q, T); // 将根节点入队
BiTree e; // 出队接受元素
while (!isEmpty(Q)) { // 队列不空则继续循环
dequeue(Q, e); // 出队一个节点
visit(e->data); // 访问节点数据
if (e->lchild != NULL) {
enqueue(Q, e->lchild); // 左孩子不为空,则入队
}
if (e->rchild != NULL) {
enqueue(Q, e->rchild); // 右孩子不为空,则入队
}
// 判断front和p是不是相等,相等则说明一层遍历完成
if (p == Q.front) {
p = Q.rear; // p指针移动到队列末尾
h++; // 层数增加
}
}
return h; // 返回树的高度
}非递归主要是判断当前是第几层。
2、计算二叉树的全部双分支节点个数
// 计算二叉树中所有双分支节点(即同时具有左孩子和右孩子的节点)的个数
int DNode(BiTree T) {
if (T == NULL) {
return 0; // 如果当前节点为空,则返回0,不计入双分支节点个数
} else {
// 判断当前节点是否同时具有左孩子和右孩子节点
int count = (T->lchild != NULL && T->rchild != NULL) ? 1 : 0;
// 返回当前节点的双分支计数(如果当前节点是双分支,则为1,否则为0),
// 加上左子树和右子树中双分支节点的个数
return count + DNode(T->lchild) + DNode(T->rchild);
}
}3、求二叉树的叶子节点个数
//求叶子结点个数
int leavel(BiTree T){
if(T ==NULL){
return 0;
}else{
//判断当前节点的左后孩子是不是空.如果为空的话表示当前节点是个叶子节点
int lcount = (T->lchild == NULL && T->rchild == NULL)?1:0;
return lcount+=leavel(T->lchild)+leavel(T->rchild);
}
}4、求二叉树全部节点的个数
int AllNode(BiTree T) {
// 函数出口
if (T == NULL) {
return 0;
} else if (T->lchild == NULL && T->rchild == NULL) {
// 如果节点是叶子节点
return 1;
} else {
// 递归计算左子树和右子树的节点数,然后加1(当前节点)
return 1 + AllNode(T->lchild) + AllNode(T->rchild);
}
}5、先序遍历二叉树找第K个元素
// 全局变量,用于记录当前遍历到的节点序号
int n = 0;
// 函数:在二叉树的先序遍历中找到第 K 个元素
int preTree_K(BiTree T, int k) {
if (T == NULL) {
return 0; // 如果当前节点为空,返回0(或者可以定义一个错误码)
} else {
++n; // 每次访问节点时,先递增节点序号
// 检查当前节点是否是第 K 个节点
if (k == n) {
return T->data; // 如果是,返回该节点的数据
}
preTree_K(T->lchild, k); // 递归遍历左子树
preTree_K(T->rchild, k); // 递归遍历右子树
}
}6、二叉树交换所有结点的左右子树
// 交换一个节点的左右子树的函数
void swapNode(BiTree node) {
if (node == NULL) {
return; // 如果节点为空,则直接返回
} else {
BiTree temp; // 用于交换的临时指针
temp = node->lchild; // 保存左子树
node->lchild = node->rchild; // 将右子树赋值给左子树
node->rchild = temp; // 将保存的左子树赋值给右子树
}
}
// 递归地交换二叉树中每个节点的左右子树的函数
void swapTree(BiTree T) {
if (T == NULL) {
return; // 如果节点为空,则直接返回
} else {
swapNode(T); // 交换当前节点的左右子树
swapTree(T->lchild); // 递归地对左子树进行相同的操作
swapTree(T->rchild); // 递归地对右子树进行相同的操作
}
}7、二叉树中打印值为X结点的所有祖先
int top = -1; // 定义栈顶指针top,并初始化为-1,表示栈为空
int p[20]; // 定义一个大小为20的数组p,用于存储节点的祖先
void allparent(BiTree T, ElemType x) { // 函数allparent,接受一个二叉树T和一个元素类型ElemType的x作为参数
if (T == NULL) { // 如果当前节点为空
return; // 直接返回,不进行任何操作
} else {
// 入栈
++top; // 栈顶指针加1,为新节点腾出空间
p[top] = T->data; // 将当前节点的数据存储到栈中
// 先递归左子树
allparent(T->lchild, x); // 递归调用allparent函数,查找左子树中是否存在目标节点x
// 如果当前节点是目标节点,则打印所有祖先
if (T->data == x) { // 如果当前节点的数据等于目标节点x
for (int i = 0; i <= top; i++) { // 注意这里应该是小于等于top,因为数组下标是从0开始的
cout << p[i] << " "; // 遍历栈,打印出所有祖先节点
}
cout << endl; // 打印换行符
}
// 再递归右子树
allparent(T->rchild, x); // 递归调用allparent函数,查找右子树中是否存在目标节点x
// 出栈
--top; // 栈顶指针减1,表示当前节点的祖先查找完成,从栈中移除
}
}8、给定结点在二叉排序树中的层次
// 查找节点x的层次
int Level_x(BiTree T, ElemType e, int level) {
if (T == NULL) {
return -1; // 如果当前节点为空,返回-1表示没有找到节点
}
if (T->data == e) {
return level; // 如果当前节点的数据等于目标节点e,返回当前层级
}
int leftLevel = Level_x(T->lchild, e, level + 1); // 递归调用Level_x函数,查找左子树中是否存在目标节点e,并增加层级
if (leftLevel != -1) {
return leftLevel; // 如果在左子树中找到了目标节点,返回其层级
}
int rightLevel = Level_x(T->rchild, e, level + 1); // 递归调用Level_x函数,查找右子树中是否存在目标节点e,并增加层级
return rightLevel; // 返回右子树中找到的目标节点层级,如果也没有找到则返回-1
}9、判断是否为完全二叉树
bool IsComplete(BiTree T) {
// 本算法判断给定二叉树是否为完全二叉树
InitQueue(Q); // 初始化队列Q,用于层序遍历二叉树
if (!T) // 如果二叉树为空
return true; // 空树被认为是完全二叉树
EnQueue(Q, T); // 将根节点T入队列
while (!IsEmpty(Q)) { // 当队列不为空时,继续循环
DeQueue(Q, p); // 从队列中出队一个节点,存储在p中
if (p) { // 如果当前节点p非空
EnQueue(Q, p->lchild); // 将p的左孩子入队列
EnQueue(Q, p->rchild); // 将p的右孩子入队列
} else { // 如果当前节点p为空
while (!IsEmpty(Q)) { // 继续循环,直到队列为空
DeQueue(Q, p); // 从队列中出队一个节点,存储在p中
if (p) { // 如果出队的节点p非空
return false; // 发现非空节点,说明不是完全二叉树,返回false
}
}
// 如果所有后续节点都为空,跳出循环,继续检查下一层
}
}
return true; // 如果所有节点都处理完毕,没有发现非空节点在空节点之后,是完全二叉树
}10、逆层序遍历二叉树
void level(BiTree T) {
if (T == NULL) {
return; // 如果二叉树为空,直接返回
}
Queue Q; // 定义队列Q,用于层序遍历
initQueue(Q); // 初始化队列Q
Stack S; // 定义栈S,用于存储层序遍历的结果
initStack(S); // 初始化栈S
BiTree e; // 定义一个临时节点指针e,用于接受出队元素
EnQueue(Q, T); // 将根节点T入队列
while (!isEmpty(Q)) { // 当队列不为空时,进行层序遍历
DeQueue(Q, e); // 从队列中出队一个节点,存储在e中
push(S, e); // 将出队的节点e入栈,用于后续逆序输出
if (e->lchild) {
EnQueue(Q, e->lchild); // 如果存在左孩子,将左孩子入队
}
if (e->rchild) {
EnQueue(Q, e->rchild); // 如果存在右孩子,将右孩子入队
}
}
while (!isEmpty(S)) { // 当栈不为空时,输出节点数据
pop(S, e); // 从栈中出栈一个节点,存储在e中
cout << e->data << endl; // 输出节点e的数据
}
}11、递归求树的宽度
// 递归求树宽度
int width[10] = {0}; // 层数
void pre(BiTree T, int level) { // level 标注当前节点是第几层的
if (T == NULL) {
return;
} else {
// 第一次访问节点,当前层数的节点数+1
width[level]++;
pre(T->lchild, level + 1);
pre(T->rchild, level + 1);
}
}
void getWidth(BiTree T) {
int max = 0;
pre(T, 0);
for (int i = 0; i < 10; i++) {
if (max < width[i]) {
max = width[i];
}
}
printf("二叉树的宽度是:%d", max);
}12、 满二叉树已知先序序列,求后序序列(暂放)
13、 已知先序和中序建立二叉链表(暂放)
// 定义创建二叉树的函数,接受先序和中序遍历数组及其索引范围
BiTree createTree(int pre[], int mid[], int l1, int h1, int l2, int h2) {
// 如果先序或中序数组的索引范围无效,则返回NULL,表示没有树可以创建
if (l1 > h1 || l2 > h2) {
return NULL;
}
// 先创建根节点
BiTree T = new BiTNode; // 分配新的二叉树节点
T->data = pre[l1]; // 先序遍历的第一个元素是根节点的值
// 在中序遍历中找到根节点的位置
int i;
for (i = l2; i <= h2; i++) {
if (mid[i] == T->data) {
break; // 找到根节点在中序遍历中的位置
}
}
// 计算左子树和右子树的长度
int left_len = i - l2; // 左子树的长度
int right_len = h2 - i; // 右子树的长度
// 递归创建左子树
if (left_len != 0) {
T->lchild = createTree(pre, mid, l1 + 1, l1 + left_len, l2, i - 1); // 先序和中序的左子树范围
} else {
T->lchild = NULL; // 如果没有左子树,则设置为空
}
// 递归创建右子树
if (right_len != 0) {
T->rchild = createTree(pre, mid, l1 + left_len + 1, h1, i + 1, h2); // 先序和中序的右子树范围
} else {
T->rchild = NULL; // 如果没有右子树,则设置为空
}
// 返回创建的二叉树的根节点
return T;
}14、树与二叉树-以兄弟链表存储,用递归求树的深度
// 定义计算二叉树高度的函数,接受二叉树的根节点作为参数
int getHight(BiTree T) {
int hc; // 左子树的高度
int hs; // 右子树的高度
// 如果树为空(即根节点为空),则高度为0
if (T == NULL) {
return 0;
} else {
// 递归计算左子树的高度
hc= getHight(T->firshchild);
// 递归计算右子树的高度
hs= getHight(T->nextsibling);
}
// 比较左右子树的高度,取较大的高度,并加1(当前节点的高度)
if (hc+ 1 > hs) {
return hc+ 1; // 如果左子树的高度大于右子树,则返回左子树高度加1
} else {
return hs; // 如果右子树的高度大于或等于左子树,则返回右子树高度加1
}
}15、 将给定的表达式树转中缀表达式
// 将给定的表达式树转换为中缀表达式
void convert(BiTree T, int deep) {
// 如果当前节点为空,直接返回,不进行任何操作
if (T == NULL) {
return;
}
// 如果当前节点是叶子节点(没有左右子节点),输出叶子节点的数据
else if (T->lchild == NULL && T->rchild == NULL) {
cout << T->data; // 输出叶子节点的数据,通常是操作数
}
// 如果当前节点不是叶子节点,即它是运算符节点
else {
// 如果当前节点的深度大于1,意味着它不是根节点,输出左括号以保证运算顺序
if (deep > 1) {
cout << "(";
}
// 递归转换左子树,深度加1,以正确处理多层嵌套的表达式
convert(T->lchild, deep + 1);
// 输出当前节点的数据,即运算符
cout << T->data;
// 递归转换右子树,深度加1
convert(T->rchild, deep + 1);
// 如果当前节点的深度大于1,输出右括号,以确保运算顺序
if (deep > 1) {
cout << ")";
}
}
}两层加括号
16、中序线索二叉树找后序前驱(暂放)
先空着,不会
17、将叶节点按从左到右的顺序连成单链表
// 将二叉树的叶节点按从左到右的顺序链接成单链表
void Link(BiTree T, BiTree& Head, BiTree& tail) {
// 如果当前节点不为空
if (T) {
// 如果当前节点是叶子节点(既没有左孩子也没有右孩子)
if (T->lchild == NULL && T->rchild == NULL) {
// 如果链表为空(还没有头节点)
if (Head == NULL) {
Head = T; // 当前节点成为链表的头节点
tail = T; // 当前节点也成为链表的尾节点
} else { // 如果链表不为空
tail->rchild = T; // 将当前节点链接到链表的尾节点
tail = T; // 更新尾节点为当前节点
}
}
// 递归处理左子树
Link(T->lchild, Head, tail);
// 递归处理右子树
Link(T->rchild, Head, tail);
}
}18、求WPL
// 初始化加权路径长度为0
int wpl = 0;
// 定义一个函数preTree,用于计算二叉树的加权路径长度(WPL)
int preTree(BiTree T, int dep) {
// 如果当前节点为空,返回0,不增加路径长度
if (T == NULL) {
return 0;
} else {
// 如果当前节点是叶子节点
if (T->lchild == NULL && T->rchild == NULL) {
// 计算当前叶子节点的加权路径长度,并累加到wpl
// 这里假设T->data存储的是字符形式的数字,需要转换为整数
wpl += (dep - 1) * (T->data);
}
// 如果当前节点不是叶子节点,则递归计算左右子树的WPL
else {
preTree(T->lchild, dep + 1); // 递归左子树,深度加1
preTree(T->rchild, dep + 1); // 递归右子树,深度加1
}
}
// 返回当前节点的加权路径长度
return wpl;
}19、删除树中以x为根节点的子树,并释放空间
// 删除二叉树节点,并释放其占用的内存空间
void del(BiTree &T) {
// 如果当前节点为空,直接返回,不进行任何操作
if (T == NULL) {
return;
} else {
// 递归删除当前节点的左子树
del(T->lchild);
// 递归删除当前节点的右子树
del(T->rchild);
// 释放当前节点的内存
free(T);
// 将当前节点指针设置为NULL,避免野指针
T = NULL;
}
}
// 删除二叉树中所有以x为根节点的子树
void del_allx(BiTree &T, int x) {
// 如果当前节点为空,直接返回,不进行任何操作
if (T == NULL) {
return;
} else {
// 判断当前节点是否是要删除的节点
if (T->data == x) {
// 如果是,递归调用del函数删除该节点及其所有子节点
del(T);
// 删除完成后返回,不再继续遍历
return;
}
// 递归检查左子树中是否包含要删除的节点
del_allx(T->lchild, x);
// 递归检查右子树中是否包含要删除的节点
del_allx(T->rchild, x);
}
}20、寻找两个节点的最近公共祖先(有点难)
// 定义一个函数findLCA,用于在二叉树中寻找两个节点p和q的最近公共祖先
BiTree findLCA(BiTree root, ElemType p, ElemType q) {
// 如果当前节点为空,或者当前节点就是p或q,那么返回当前节点
if (root == NULL || root->data == p || root->data == q) {
return root;
}
// 递归在左子树中查找p和q的最近公共祖先
BiTree left = findLCA(root->lchild, p, q);
// 递归在右子树中查找p和q的最近公共祖先
BiTree right = findLCA(root->rchild, p, q);
// 如果在左右子树中都找到了目标节点,说明当前节点是p和q的最近公共祖先
if (left != NULL && right != NULL) {
return root;
}
// 如果只在一边找到了目标节点,那么返回找到的那一边的最近公共祖先
// left != NULL ? left : right 是一个三元运算符,如果left不为空则返回left,否则返回right
return left != NULL ? left : right;
}想不到的话还有笨方法。
BiTree data[maxsize] = {NULL}; // 初始化一个数组,用于存储二叉树的节点,初始值设为NULL
int index = 0; // 用于数组data的下标,表示当前存储的节点位置
// 定义一个函数levelOrder,用于进行二叉树的层序遍历,并找出两个节点p和q的最近公共祖先
void levelOrder(BiTree T, ElemType p, ElemType q) {
// 初始化队列Q
Queue Q;
Init(Q);
int _p, _q; // 用于存储p和q节点在数组data中的下标
// 如果根节点不为空,则将其入队
if (T != NULL) {
EnQueue(Q, T);
}
// 当队列不为空时,进行循环
while (!isEmpty(Q)) {
BiTree node;
// 从队列中出队一个节点
DeQueue(Q, node);
// 将出队的节点存储到数组data中,并更新下标index
data[++index] = node;
// 如果当前节点的数据等于p,则记录p的下标
if (node->data == p) {
_p = index;
}
// 如果当前节点的数据等于q,则记录q的下标
if (node->data == q) {
_q = index;
}
// 如果当前节点不为空,则访问该节点,并将其左右孩子入队(如果它们不为空)
if (node != NULL) {
visit(node->data); // 访问该节点,例如打印节点数据
if (node->lchild != NULL) {
EnQueue(Q, node->lchild);
}
if (node->rchild != NULL) {
DeQueue(Q, node->rchild);
}
}
}
// 通过下标计算p和q的最近公共祖先的下标
while (_p != _q) {
_p /= 2; // _p除以2,相当于在层序遍历的数组中向上移动一层
_q /= 2; // _q除以2,同理
}
// 输出p和q的最近公共祖先的节点数据
cout << p << "和" << q << "元素的祖先是:" << data[_p]->data << endl;
}21、中序遍历非递归
void InOrder2(BiTree T) { // 中序遍历的非递归算法
InitStack(S); // 初始化栈S
BiTree p = T; // 初始化指针p为根节点T
while (p || !IsEmpty(S)) { // 当栈不为空或p不为空时循环
if (p) { // 如果当前节点p不为空
Push(S, p); // 将当前节点p入栈
p = p->lchild; // 向左子树移动
} else { // 如果当前节点p为空
Pop(S, p); // 出栈,并将栈顶元素赋值给p
visit(p); // 访问当前节点,即进行某种操作,如打印
p = p->rchild; // 向右子树移动
}
}
}22、先序非递归
void PreOrderTraversal(BiTree T) { // 先序遍历的非递归算法
InitStack(S); // 初始化栈S
BiTree p = T; // 初始化指针p为根节点T
while (p || !IsEmpty(S)) { // 当栈不为空或p不为空时循环
if (p) { // 如果当前节点p不为空
visit(p); // 访问当前节点,例如打印节点数据
Push(S, p); // 将当前节点p入栈
p = p->lchild; // 向左子树移动
} else { // 如果当前节点p为空
Pop(S, p); // 出栈,并将栈顶元素赋值给p
p = p->rchild; // 向右子树移动
}
}
}五、串的基本操作
结构体
typedef struct str { // 顺序串的结构体
char ch[MAXSIZE + 1];
int length;
} str;1、赋值操作
// 定义一个函数StrAssign,用于将字符数组chs的值赋给串S
void StrAssign(str &S, char chs[]) {
int i = 0; // 初始化索引变量i,用于遍历字符数组chs
// 循环遍历字符数组chs,直到遇到字符串结束符'\0'
while (chs[i] != '\0') {
// 将字符数组chs中的字符逐个赋值给串S的数据成员ch
S.ch[i] = chs[i];
// 索引i自增,移动到字符数组的下一个字符
i++;
}
// 当循环结束时,索引i等于字符数组chs的长度
// 将计算出的长度赋值给串S的长度成员length
S.length = i;
}2、复制操作
// 定义一个函数StrCopy,用于将串T的值复制到串S中
void StrCopy(str &S, str &T) {
// 使用for循环遍历串T中的每个字符
for (int i = 0; i < T.length; i++) {
// 将串T中的字符逐个复制到串S的对应位置
S.ch[i] = T.ch[i];
}
// 在串S的字符数组的末尾添加字符串结束符'\0',确保字符串正确结束
S.ch[T.length] = '\0';
// 将串T的长度复制到串S的长度成员中
S.length = T.length;
}3、判断字符串是不是空串
// 判断字符串是不是空串
bool IsStrEmpty( str S) {
return S.length == 0;
}
4、比较操作
// 定义一个函数StrCompare,用于比较两个字符串S和T的大小
int StrCompare(str &S, str &T) {
// 循环比较两个字符串中对应位置的字符
for (int i = 0; i < S.length && i < T.length; i++) {
// 如果S中的字符ASCII值大于T中的字符ASCII值,返回1
if (S.ch[i] > T.ch[i]) return 1;
// 如果S中的字符ASCII值小于T中的字符ASCII值,返回-1
if (S.ch[i] < T.ch[i]) return -1;
}
// 如果S的长度大于T的长度,返回1
if (S.length > T.length) return 1;
// 如果S的长度小于T的长度,返回-1
if (S.length < T.length) return -1;
// 如果上述条件都不满足,说明两个字符串相等,返回0
return 0;
}5、求串长
//求字符串的长度
int StrLength( str S) {
return S.length;
}6、求子串
// 定义一个函数SubSting,用于从字符串S中提取从位置pos开始的长度为len的子串,并存储到Sub中
void SubSting(str &Sub, str S, int pos, int len) {
// 首先检查字符串S是否为空
if (IsStrEmpty(S)) {
return;
}
// 检查pos和len是否合理,即pos是否在字符串范围内,len是否非负,以及子串是否会超出原字符串的范围
if (pos < 1 || pos > S.length || len < 0 || (pos + len - 1 > S.length)) {
cout << "输入有误!" << endl; // 如果输入有误,输出错误信息
return;
}
int i, j; // 定义两个索引变量i和j,i用于遍历原字符串S,j用于遍历子串Sub
// 循环从S中提取子串,i从pos-1开始(因为数组索引从0开始),j从0开始
for (i = pos - 1, j = 0; i < pos + len - 1 && i < S.length; i++, j++) {
Sub.ch[j] = S.ch[i]; // 将S中的字符赋值给Sub
}
Sub.ch[j] = '\0'; // 在Sub的末尾添加字符串结束符'\0',确保子串正确结束
Sub.length = j; // 更新Sub的长度为实际提取的字符数
}7、串连接
// 定义一个函数Concat,用于将两个字符串S3和S4连接起来,并将结果存储在T1中
void Concat(str &T1, str &S3, str &S4) {
// 如果S3和S4都是空串,那么T1也将是一个空串
if (IsStrEmpty(S3) && IsStrEmpty(S4)) {
T1.length = 0; // 设置T1的长度为0
T1.ch[0] = '\0'; // 确保空串以'\0'结尾
return; // 结束函数执行
}
int i; // 定义索引变量i,用于遍历S3
// 将S3中的字符复制到T1中
for (i = 0; i < S3.length; i++) {
T1.ch[i] = S3.ch[i];
}
int j; // 定义索引变量j,用于遍历S4
// 将S4中的字符复制到T1中,紧接在S3的字符之后
for (j = 0; j < S4.length; j++, i++) { // j从0开始,i从S3.length开始
T1.ch[i] = S4.ch[j];
}
T1.ch[i] = '\0'; // 在T1的末尾添加字符串结束符'\0',确保连接后的串正确结束
T1.length = i; // 更新T1的长度,i此时是连接后字符串的最后一个字符的索引
}8、定位
// 定义一个函数Index,用于在字符串S5中查找子串S6的起始位置
int Index(str &S5, str &S6) {
// 如果S6是空串或者S5的长度小于S6的长度,则返回0或-1
if (IsStrEmpty(S6) || S5.length < S6.length) {
return -1; // 返回-1表示子串不在主串中
}
int i = 0, j = 0; // i用于遍历S5,j用于遍历S6
// 使用while循环进行查找
while (i < S5.length && j < S6.length) {
// 如果S5和S6在当前位置的字符相同,则两个索引都向前移动
if (S5.ch[i] == S6.ch[j]) {
i++;
j++;
} else {
// 如果字符不匹配,i保持不变,j重置为0,重新开始匹配S6的起始字符
j = 0;
}
}
// 如果j等于S6的长度,说明S6已经在S5中完全匹配
if (j == S6.length) {
return i - j; // 返回匹配的起始位置,注意这里的返回值应该是i - j,因为i和j在最后一次匹配时是同步的
} else {
// 如果S6没有在S5中找到,返回-1
return -1;
}
}六、栈、队列和数组
1、链式栈(带头)
#include<stdio.h>
#include<stdlib.h>
#include <iostream>
#include <cstdlib>
using namespace std;
typedef struct LinkNode{
int data; // 栈顶元素
struct LinkNode* next; // 栈顶指针
}LinkNode,*LinkStack;
// 链栈初始化(带头节点)
LinkStack Init(){
// 创建头节点
LinkStack S = (LinkStack) malloc(sizeof(LinkNode));
S->data = 0;
S->next = NULL;
return S; // 返回头节点
}
// 判断链式栈是不是空
bool isEmpty(LinkStack S){
if(S->next == NULL){
return true;
}
return false;
}
// 链栈入栈
void push(LinkStack &S, int data){
// 创建新节点
LinkStack p = (LinkStack)malloc(sizeof(LinkNode));
p->data = data;
p->next = S->next;
S->next = p;
}
// 链式栈出栈
void pop(LinkStack &S){
// 链式栈不需要沾满判断
LinkStack p = S->next;
if(p==NULL){
cout<<"当前栈为空"<<endl;
}else{
cout<<"栈顶元素出栈:"<<p->data<<endl;
S->next = p->next;
free(p);
}
}
//链式栈取栈顶元素
int getTop(LinkStack &S){
LinkStack p = S->next;
if(isEmpty(S)){
cout<<"链式栈为空"<<endl;
}else{
return p->data;
}
}
//链式栈求栈的长度(元素的个数)
int getCount(LinkStack S){
int count = 0;
LinkStack p = S->next;
while(p!=NULL){
count++;
p = p->next;
}
return count;
}
int main(){
LinkStack S;
S = Init(); // 初始化链栈并接收返回值
push(S, 2);
push(S, 3);
push(S, 9);
push(S, 7);
// while(!isEmpty(S)) pop(S); // 循环直到栈为空
cout<<"栈顶元素是:"<<getTop(S)<<endl;
cout<<"栈中元素个数:"<<getCount(S)<<endl;
return 0;
}
2、链式栈(无头)
#include<stdio.h>
#include<stdlib.h>
#include <iostream>
#include <cstdlib>
using namespace std;
typedef struct LinkNode{
int data; // 栈顶元素
struct LinkNode* next; // 栈顶指针
}LinkNode,*LinkStack;
// 链栈初始化(不带头节点)
void Init(LinkStack &S){
S = NULL;
}
// 判断链式栈是不是空
bool isEmpty(LinkStack S){
if(S == NULL){
return true;
}
return false;
}
// 链栈入栈
void push(LinkStack &S, int data){
// 创建新节点
LinkStack p = (LinkStack)malloc(sizeof(LinkNode));
p->data = data;
p->next = S;
S = p;
}
// 链式栈出栈
void pop(LinkStack &S,ElemType &e){
// 链式栈不需要沾满判断
LinkStack p = S;
if(p==NULL){
cout<<"当前栈为空"<<endl;
}else{
e = p->data;
S = p->next;
free(p);
}
}
//链式栈取栈顶元素
int getTop(LinkStack &S){
LinkStack p = S;
if(isEmpty(S)){
cout<<"链式栈为空"<<endl;
}else{
return p->data;
}
}
//链式栈求栈的长度(元素的个数)
int getCount(LinkStack S){
int count = 0;
LinkStack p = S;
while(p!=NULL){
count++;
p = p->next;
}
return count;
}
int main(){
LinkStack S;
Init(S); // 初始化链栈并接收返回值
push(S, 2);
push(S, 3);
push(S, 9);
push(S, 7);
// while(!isEmpty(S)) pop(S); // 循环直到栈为空
cout<<"栈顶元素是:"<<getTop(S)<<endl;
cout<<"栈中元素个数:"<<getCount(S)<<endl;
return 0;
}
3、顺序循环队列
#include <iostream>
#include <cstdlib>
using namespace std;
// 定义顺序队列的最大容量
const int MAX_SIZE = 100;
// 定义顺序队列的类型
typedef struct {
int data[MAX_SIZE]; // 存储队列元素的数组
int front; // 队列头指针
int rear; // 队列尾指针
} SeqQueue;
// 初始化顺序队列
void init(SeqQueue& Q) {
Q.front = Q.rear = 0; // 初始化头尾指针为0
}
// 判断顺序队列是否为空
bool isEmpty(SeqQueue Q) {
return Q.front == Q.rear;
}
// 判断顺序队列是否已满
bool isFull(SeqQueue Q) {
return (Q.rear + 1) % MAX_SIZE == Q.front;
}
//获取循环队列的元素的个数
int getLength(Queue Q){
return (Q.rear-Q.front+MAX_SIZE)%MAX_SIZE;
}
// 入队操作
bool EnQueue(SeqQueue& Q, int data) {
if (isFull(Q)) {
cout << "队列已满,无法入队!" << endl;
return false;
}
Q.data[Q.rear] = data; // 将元素放入队尾
Q.rear = (Q.rear + 1) % MAX_SIZE; // 更新队尾指针,循环使用
return true;
}
// 出队操作
bool DeQueue(SeqQueue& Q, int& data) {
if (isEmpty(Q)) {
cout << "队列为空,无法出队!" << endl;
return false;
}
data = Q.data[Q.front]; // 获取队头元素
Q.front = (Q.front + 1) % MAX_SIZE; // 更新队头指针,循环使用
return true;
}
// 主函数,用于演示顺序队列的操作
int main() {
SeqQueue Q;
init(Q);
EnQueue(Q, 1);
EnQueue(Q, 2);
EnQueue(Q, 3);
int data;
while (DeQueue(Q, data)) {
cout << "出队元素: " << data << endl;
}
return 0;
}4、使用tag表示循环队列是不是满了
#include <iostream>
#include <cstdlib>
#include <stdio.h>
#include <stdlib.h>
using namespace std;
#define maxsize 4 // 定义队列的最大容量
typedef int ElemType; // 定义队列元素的数据类型为int
// 循环队列的结构体定义
typedef struct {
ElemType data[maxsize]; // 存储队列元素的数组
int front, rear; // 队列的头和尾指针
int tag; // 用于标记队列是否为空或满,0表示空,1表示非空
} SqQueue;
// 循环队列初始化函数
void init(SqQueue &Q) {
Q.front = Q.rear = 0; // 初始化头尾指针
Q.tag = 0; // 标记队列为空
}
// 循环队列判断是否为空的函数
int judge(SqQueue &Q) {
// 如果队列为空,返回1,否则返回0
return Q.tag == 0 && Q.front == Q.rear;
}
// 循环队列判断是否为满的函数
int isFull(SqQueue &Q) {
// 如果队列为满,返回1,否则返回0
return Q.tag == 1 && Q.front == Q.rear;
}
// 循环队列入队函数
void push(SqQueue &Q, ElemType e) {
if (isFull(Q)) { // 如果队列满,输出提示信息并返回
cout << "满了" << endl;
return;
}
Q.data[Q.rear] = e; // 将元素e放入队尾
Q.rear = (Q.rear + 1) % maxsize; // 队尾指针后移
Q.tag = 1; // 标记队列非空
}
// 循环队列出队函数
void pop(SqQueue &Q, ElemType &e) {
if (judge(Q)) { // 如果队列为空,输出提示信息并返回
cout << "空" << endl;
return;
}
e = Q.data[Q.front]; // 将队头元素赋值给e
Q.front = (Q.front + 1) % maxsize; // 队头指针后移
Q.tag = 0; // 标记队列可能为空
}
int main() {
SqQueue Q; // 创建循环队列Q
init(Q); // 初始化队列
push(Q, 1); push(Q, 2); push(Q, 3); push(Q, 4); // 入队操作
ElemType e; // 用于接收出队元素
pop(Q, e); // 出队操作
cout << "出队元素:" << endl; // 输出出队元素提示信息
cout << e; // 输出出队元素的值
return 0;
}5、链式队列
#include <iostream>
#include <cstdlib>
using namespace std;
// 定义链式队列的节点结构体
typedef struct LinkNode {
int data;
struct LinkNode* next;
} LinkNode;
// 定义链式队列的类型
typedef struct {
LinkNode* front; // 队列头指针
LinkNode* rear; // 队列尾指针
} LinkQueue;
// 初始化链式队列
void init(LinkQueue &Q) {
Q.front = Q.rear = (LinkNode*)malloc(sizeof(LinkNode));
Q.front->next = NULL;
}
// 判断链式队列是否为空
bool isEmpty(LinkQueue Q) {
return Q.front == Q.rear;
}
// 入队操作
void EnQueue(LinkQueue &Q, int data) {
LinkNode* p = (LinkNode*)malloc(sizeof(LinkNode));
p->data = data;
p->next = NULL;
Q.rear->next = p;
Q.rear = p;
}
// 出队操作
bool DeQueue(LinkQueue &Q, int& data) {
if (isEmpty(Q)) {
cout << "队列为空,无法出队!" << endl;
return false;
}
LinkNode* p = Q.front->next;
data = p->data;
Q.front->next = p->next;
if (Q.rear == p) { // 如果移除的是最后一个节点,更新rear指针
Q.rear = Q.front;
}
free(p);
return true;
}
// 主函数,用于演示链式队列的操作
int main() {
LinkQueue Q;
init(Q);
EnQueue(Q, 1);
EnQueue(Q, 2);
EnQueue(Q, 3);
int data;
while (DeQueue(Q, data)) {
cout << "出队元素: " << data << endl;
}
return 0;
}6、括号匹配
// 括号匹配函数
// 该函数用于检查输入的字符串中的括号是否正确匹配
bool pp(LinkStack &S, char string[], int length) {
// 遍历字符串中的每个字符
for (int i = 0; i < length; i++) {
// 如果当前字符是左括号('{'、'(' 或 '['),则将其压入栈中
if (string[i] == '{' || string[i] == '(' || string[i] == '[') {
push(S, string[i]);
} else {
// 如果当前字符是右括号(']'、')' 或 '}')
// 首先检查栈是否为空,如果为空,则无法匹配对应的左括号,返回 false
if (S->next == NULL) {
return false; // 栈为空,无法匹配
}
// 定义一个变量 e 用于存储从栈中弹出的元素
ElemType e;
// 从栈中弹出一个元素,并将其值存储在变量 e 中
pop(S, e);
// 检查弹出的左括号与当前的右括号是否匹配
// 如果不匹配,则返回 false
if ((string[i] == ']' && e != '[') ||
(string[i] == ')' && e != '(') ||
(string[i] == '}' && e != '{')) {
return false; // 括号不匹配
}
}
}
// 遍历完成后,如果栈为空,则说明所有括号都正确匹配,返回 true
// 如果栈不为空,则说明有未匹配的左括号,返回 false
return S->next == NULL; // 栈为空,所有括号匹配成功
}七、线性表
1、逆转顺序表中的所有元素
void reserve(int A[], int n) {
int i, temp; // 定义循环变量i和临时变量temp用于交换数组元素
for(i = 0; i < n / 2; i++) { // 循环条件修正为i < n / 2,确保不会越界
temp = A[i]; // 将当前元素A[i]的值保存到临时变量temp中
A[i] = A[n - i - 1]; // 将数组末尾的元素A[n - i - 1]赋值给A[i],实现交换
A[n - i - 1] = temp; // 将temp中的值(原A[i]的值)赋值给A[n - i - 1],完成交换
}
}2、删除给定值的元素
// 删除顺序表L中值为e的元素
int del(SqList &L, int e) {
// 判断当前的顺序表是不是空的
if (L.len <= 0) {
return 0; // 如果顺序表为空,直接返回0
}
// 遍历顺序表
for (int i = 0; i < L.len; i++) { // 注意这里的循环条件应该是 i < L.len
// 如果找到值为e的元素
if (e == L.elem[i]) {
// 将找到的元素后面的所有元素向前移动一位,覆盖要删除的元素
for (int j = i + 1; j < L.len; j++) {
L.elem[j - 1] = L.elem[j];
}
L.len--; // 顺序表长度减1
return 1; // 删除成功,返回1
}
}
return 0; // 如果没有找到值为e的元素,返回0
}3、删除给定范围值的元素
// 删除顺序表L中,值在给定范围s到t之间的所有元素(假设t > s)
void del(SqList &L, int s, int t) {
// 判断顺序表是否为空
if (L.length <= 0) {
printf("不存在元素");
return;
}
// 检查s和t的值是否合法,即t是否大于s
if (!(t > s)) {
printf("元素位置不合法");
return;
}
int j = 0; // j用于记录新顺序表的长度
// 遍历顺序表
for (int i = 0; i < L.length; i++) {
// 判断当前元素是否不在s到t的范围内
if (!(L.elem[i] >= s && L.elem[i] <= t)) {
L.elem[j] = L.elem[i]; // 将不在范围内的元素复制到前面
j++; // 新顺序表长度加1
}
}
L.length = j; // 更新顺序表的长度为新长度
}4、从有序顺序表中删除其值重复的元素
// 删除有序顺序表中重复的元素
void del(SqList &L) {
// 健壮性检查:如果顺序表长度小于等于0,直接返回
if (L.length <= 0) {
return;
}
int count = 0; // 记录出现重复元素的次数
// 从第二个元素开始遍历顺序表
for (int i = 1; i < L.length; i++) {
// 如果当前元素与前一个元素相等,说明是重复元素
if (L.elem[i] == L.elem[i - 1]) {
count++; // 重复元素计数加1
} else {
// 如果当前元素与前一个元素不相等,将当前元素复制到前一个元素的位置
L.elem[i - count] = L.elem[i];
}
}
// 更新顺序表的长度,减去重复元素的数量
L.length -= count;
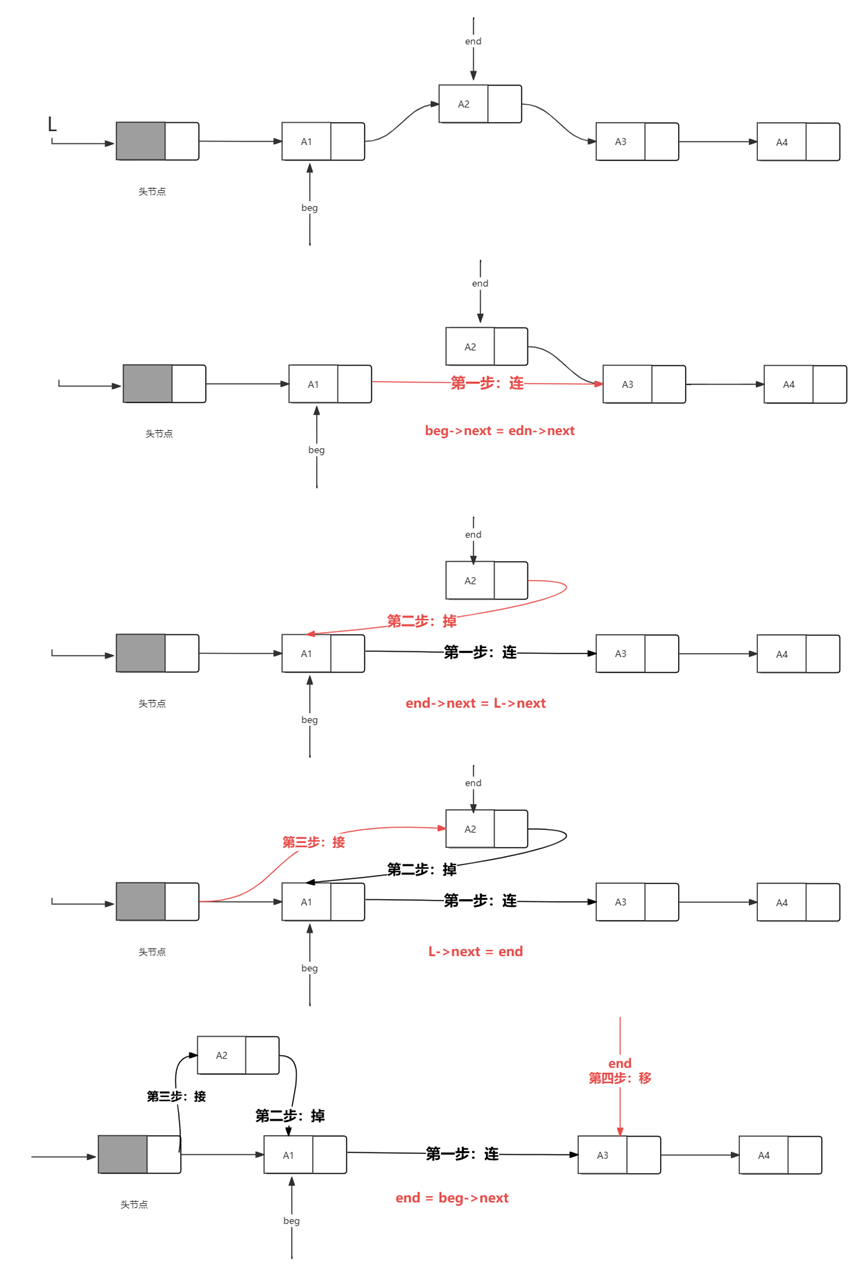
}5、带头结点的单链表“就地”逆置。
// 带头节点的单链表就地反转
LinkList reserve(LinkList &L) {
LinkList beg = L->next; // 指向原链表的第一个有数据的节点
LinkList end = L->next->next; // 指向原链表的第二个有数据的节点
// 当beg的下一个节点不为空时,进行反转操作
while (beg->next != NULL) {
beg->next = end->next; // 将beg的下一个节点指向end的下一个节点,实现反转
end->next = L->next; // 将end的下一个节点指向头节点,更新end的next为原头节点
L->next = end; // 更新头节点的next为end,即新的头节点
end = beg->next; // 更新end为新的节点,准备下一轮反转
}
// 反转完成后,返回新的头节点
return L->next;
}6、按序号奇偶,拆分单链表
// 定义一个函数,用于将链表L中的节点按照奇数和偶数位置分离到两个新链表中
void aaa(LinkList &L) {
LinkList p = L->next; // 指向链表的第一个数据节点
// 创建两个新的头节点,用于构建奇数和偶数链表
LinkList headA = (LinkList)malloc(sizeof(LNode)); // 奇数链表的头节点
LinkList headB = (LinkList)malloc(sizeof(LNode)); // 偶数链表的头节点
LinkList Aa = headA; // 用于构建奇数链表的当前节点
LinkList Bb = headB; // 用于构建偶数链表的当前节点
headA->next = NULL; // 初始化奇数链表的头节点的next为NULL
headB->next = NULL; // 初始化偶数链表的头节点的next为NULL
int index = 1; // 用于记录当前节点的位置,1表示第一个节点,即奇数位置
// 当p不为空,即链表未遍历完
while (p != NULL) {
if (index % 2 == 1) { // 如果当前是奇数个节点
Aa->next = p; // 将当前节点p链接到奇数链表的末尾
Aa = Aa->next; // 移动Aa指针到奇数链表的末尾
L->next = p->next; // 将原链表的当前节点的next移动到下一个节点
p->next = NULL; // 将当前节点p的next设置为NULL,断开与原链表的连接
p = L->next; // 移动p指针到原链表的下一个节点
} else { // 如果当前是偶数个节点
Bb->next = p; // 将当前节点p链接到偶数链表的末尾
Bb = Bb->next; // 移动Bb指针到偶数链表的末尾
L->next = p->next; // 将原链表的当前节点的next移动到下一个节点
p->next = NULL; // 将当前节点p的next设置为NULL,断开与原链表的连接
p = L->next; // 移动p指针到原链表的下一个节点
}
index++; // 节点位置计数加1
}
// 打印奇数序列
printf("奇数序列:\n");
printList(headA); // 假设printList是一个打印链表的函数
printf("\n");
// 打印偶数序列
printf("偶数序列:\n");
printList(headB); // 假设printList是一个打印链表的函数
}7、链表中的节点交替逆序排列
// 定义一个函数,用于对单链表L进行重排序
void reSort(LinkList &L) {
// 初始化指针p和q,p走一步,q走两步
LinkList p = L->next;
LinkList q = L->next;
LinkList r;
// 当q未走到链表尾部时,继续循环
while (q->next != NULL) {
p = p->next; // p走一步
q = q->next; // q走一步
// 如果q还有下一个节点,q再走一步
if (q->next != NULL) {
q = q->next;
}
}
// 此时,q指向链表的尾部,p指向链表的中间位置
// 创建一个新节点作为重排序后链表的头节点
q = p->next;
p->next = NULL; // 断开原链表,准备重排序
// 使用前插法逆置q指向的链表后半段
while (q != NULL) {
r = q->next; // 保存q的下一个节点
q->next = p->next; // 将q的下一个节点指向p的下一个节点
p->next = q; // 将p的下一个节点指向q
q = r; // q移动到下一个节点
}
// 将逆置后的后半段链表与前半段链表合并
LinkList s = L->next;
p->next = q; // 将前半段链表的末尾节点指向逆置后的后半段链表的头节点
p->next = NULL; // 重置p的next为NULL,准备合并前半段链表
while (q != NULL) {
r = q->next; // 保存q的下一个节点
q->next = s->next; // 将q的下一个节点指向s的下一个节点
s->next = q; // 将s的下一个节点指向q
s = q->next; // s移动到下一个节点
q = r; // q移动到下一个节点
}
// 打印重排序后的链表
printList(L);
}8、单链表找倒数第k个位置上的结点
// 定义一个函数Search_K,用于在单链表L中查找倒数第k个元素
int Search_K(LinkList L, int k) {
LinkList p = L->next, q = L->next; // 初始化两个指针p和q,都指向链表的第一个数据节点
int count = 0; // 用于记录步数
// 当p不为空时,继续循环
while (p != NULL) {
if (count < k) {
count++; // 增加步数
p = p->next; // p先走k步,使得p和q之间相差k个元素
} else {
q = q->next; // p走完k步后,q开始移动,与p一起往后走
p = p->next;
}
}
// 如果count小于k,说明在走到k步之前链表已经结束,不存在倒数第k个节点
if (count < k) {
return 0; // 返回0表示未找到
} else {
return p->data; //返回倒数第k个节点的值。
}
}9、单链表,删除绝对值相等的结点,只保留第一次出现的
// 定义一个函数aaa,用于删除单链表L中的重复元素
void aaa(LinkList &L) {
// 创建辅助数组,用于标记元素是否已经出现过
int fuzhu[20] = {0}; // 默认数组中每个元素的值是0,表示元素未出现过
// 初始化指针p指向链表的头节点
LinkList p = L;
LinkList r = NULL; // 指向要删除的节点
int index; // 数组下标
// 循环遍历链表,直到p的下一个节点为空
while (p->next != NULL) {
// 取出data转为正数,用于作为辅助数组的下标
index = (p->next->data < 0) ? (-(p->next->data)) : (p->next->data);
// 如果该元素未在辅助数组中标记为出现过
if (fuzhu[index] == 0) {
fuzhu[index] = 1; // 标记该元素已出现
p = p->next; // 移动p到下一个节点
} else { // 如果该元素已经出现过,即第二次出现
r = p->next; // 保存要删除的节点
p->next = r->next; // 删除元素,将p的next指向r的下一个节点
free(r); // 释放要删除节点的内存
}
}
// 打印单链表,显示删除重复元素后的结果
printList(L);
}10、按递增顺序输出单链表元素,并删除最小元素。
// 定义一个函数minDel,用于按递增顺序输出单链表L的元素,并删除最小元素
void minDel(LinkList &L) {
LinkList pre = NULL; // pre指向被删除元素的前驱节点
LinkList p = NULL; // 工作指针,用于遍历链表
LinkList q = NULL; // 指向待删除的节点
// 当链表不为空时,执行循环
while (L->next != NULL) {
pre = L; // pre初始化指向链表的头节点
p = pre->next; // p初始化指向链表的第一个数据节点
// 遍历链表,寻找最小元素
while (p->next != NULL) {
// 如果找到更小的元素,更新pre指向更小元素的前驱节点
if (p->next->data < pre->next->data) {
pre = p;
}
p = p->next; // 移动p指针到下一个节点
}
// 输出最小元素
printf("本次最小的节点是: %d\n", pre->next->data);
// 删除最小元素
q = pre->next; // q指向最小元素
pre->next = q->next; // 从链表中删除最小元素
free(q); // 释放最小元素节点的内存
// 输出链表,显示删除最小元素后的结果
printList(L);
printf("\n"); // 打印换行符,为下一次输出做准备
}
}11、递归删除不带头结点单链表中值为x的结点
// 定义一个函数Del_x,用于在单链表L中删除值为x的所有节点
void Del_x(LinkList &L, int x) {
LinkList p; // 定义一个指针p,用于指向要删除的节点
// 如果链表为空,直接返回,因为没有节点可以删除
if (L == NULL) {
return;
}
// 如果当前节点的数据等于x,说明找到了要删除的节点
if (L->data == x) {
p = L; // 将p指向要删除的节点
L = L->next; // 将头指针L移动到下一个节点,绕过要删除的节点
free(p); // 释放要删除节点的内存
Del_x(L, x); // 递归调用Del_x,继续在剩余链表中查找并删除值为x的节点
} else {
// 如果当前节点的数据不等于x,说明当前节点不是要删除的节点
// 递归调用Del_x,继续在下一个节点中查找值为x的节点
Del_x(L->next, x);
}
}注意这个地方不会产生断链,因为在Del_x(L->next,x);函数中我们传的是L的下一个节点的地址不是L。
12、给定两个升序单链表 ,将其合并后仍为升序并输出。
// 假设L1、L2有头节点
void resort(LinkList &L1, LinkList &L2) {
// p1指向L1的第一个数据节点
LinkList p1 = L1->next;
// p2指向L2的第一个数据节点
LinkList p2 = L2->next;
// q1和q2用于临时存储节点的下一个节点
LinkList q1, q2;
// 遍历L2,直到p2为NULL,即L2的末尾
while(p2 != NULL) {
// 如果p2指向的节点的数据大于等于p1指向的节点的数据
if(p2->data >= p1->data) {
// 保存p1的下一个节点
q1 = p1->next;
// 将p2插入到p1的前面
p1->next = p2;
// 保存p2的下一个节点
q2 = p2->next;
// 将p2的next指向q1,即p1原来指向的节点
p2->next = q1;
}
// p1移动到下一个节点
p1 = q1;
// p2移动到下一个节点
p2 = q2;
}
}13、顺序表逆置
void reserve(int A[], int n) {
int i, temp; // 定义循环变量i和临时变量temp用于交换数组元素
// 遍历数组的前半部分,将每个元素与其对应的后半部分元素交换
// 循环条件修正为i < n / 2,确保不会越界
for(i = 0; i < n / 2; i++) {
temp = A[i]; // 保存当前元素的值
A[i] = A[n - i - 1]; // 将当前元素与对应的后半部分元素交换
A[n - i - 1] = temp; // 将后半部分元素的值赋给当前位置
}
// 遍历数组并打印每个元素,展示数组反转后的结果
for(i = 0; i < n; i++) {
printf("%d ", A[i]); // 打印当前元素
}
}14、删除顺序表中所有值为x的元素
// 删除顺序表中全部的值为x的元素,时间复杂度为n
void del_x(SqList &L, ElemType e) {
if (L.length == 0) {
cout << "顺序表为空" << endl; // 如果顺序表为空,则输出提示信息并返回
return;
}
int k = 0; // k用于记录不为要删除元素的位置
// 遍历顺序表中的每个元素
for (int i = 0; i < L.length; i++) {
if (L.data[i] != e) {
L.data[k] = L.data[i]; // 如果当前元素不等于要删除的元素,则将其复制到k的位置
k++; // 增加k的值,指向下一个可能的非删除元素的位置
}
}
L.length = k; // 更新顺序表的长度,排除所有被删除的元素
}15、将两个有序的顺序表合并为一个
// 将两个有序顺序表L1和L2合并为一个有序顺序表L3
void merge(SqList L1, SqList L2, SqList &L3) {
int i = 0; // L1的下标
int j = 0; // L2的下标
int k = 0; // L3的下标
// 合并两个有序表,直到其中一个表的元素全部被合并完
while (i < L1.length && j < L2.length) {
if (L1.data[i] <= L2.data[j]) {
L3.data[k++] = L1.data[i++]; // 将L1中的较小元素放入L3,并移动L1的下标
} else {
L3.data[k++] = L2.data[j++]; // 将L2中的较小元素放入L3,并移动L2的下标
}
}
//有剩下的说明都是最大的几个了
// 如果L1还有剩余元素,将它们全部复制到L3
while (i != L1.length) {
L3.data[k++] = L1.data[i++];
}
// 如果L2还有剩余元素,将它们全部复制到L3
while (j != L2.length) {
L3.data[k++] = L2.data[j++];
}
L3.length = k; // 更新L3的长度,即合并后有序表的长度
}
16、在有序的顺序表中查找特定元素,存在则与其后元素交换,不存在则插入该元素,顺序表始终有序。
// 折半算法
void find_x2(SqList &L, ElemType x) {
if (L.length == 0) {
cout << "kong" << endl; // 如果顺序表为空,则输出提示信息
}
bool found = false; // 标记是否找到元素
int low = 0; // 定义查找范围的下界
int high = L.length - 1; // 定义查找范围的上界
int mid; // 定义中间位置
int temp; //中间变量
// 使用折半查找法查找元素x
while (low <= high) {
mid = (low + high) / 2; // 计算中间位置
if (L.data[mid] == x) {
found = true;
break; // 如果找到元素,则跳出循环
} else if (x > L.data[mid]) {
low = mid + 1; // 调整查找范围的下界
} else {
high = mid - 1; // 调整查找范围的上界
}
}
int j; // 定义插入位置的下标
if (!found) { // 如果未找到该元素
for (j = L.length - 1; j >= 0; j--) { // 从后向前查找插入位置
if (L.data[j] > x) {
L.data[j + 1] = L.data[j]; // 将元素向后移动
}
}
L.data[j + 1] = x; // 插入新元素
L.length++; // 更新顺序表长度
}else{ //找到元素了位置是mid和后面的元素交换位置。
temp = A[mid];
A[mid] = A[mid+1];
A[mid+1] = temp;
}
}17、单链表删除值为x的元素,元素个数不唯一。
void Del_X_1(LinkList &L, ElemType x) {
LNode *p = L->next; // p指向链表的第一个结点(头结点的下一个结点)
LNode *pre = L; // pre指向头结点
LNode *q; // q用于临时存储要删除的结点
while (p != NULL) { // 遍历链表直到末尾
if (p->data == x) { // 如果当前结点的数据等于要删除的数据x
q = p; // q指向要删除的结点
p = p->next; // p移动到下一个结点
pre->next = p; // 将前一个结点的next指向p,从而删除q结点
free(q); // 释放q结点占用的内存
} else { // 如果当前结点的数据不等于x
p = p->next; // p继续移动到下一个结点
pre = pre->next; // pre也移动到下一个结点
}
}
}18、单链表删除最小的元素,该元素唯一。
#include <iostream>
typedef struct LNode {
int data;
struct LNode *next;
} LNode, *LinkList;
// 删除单链表中最小元素的函数
void del_min(LinkList &L) {
if (L == NULL || L->next == NULL) {
std::cout << "链表为空或只有一个元素,无法删除最小元素。" << std::endl;
return;
}
// 初始化两个指针p和q,都指向链表的第一个节点
LinkList pre = L;
LinkList p = L->next;
LinkList q = L; // q也指向第一个节点,用于跟踪最小元素的前驱节点
LinkList s; // 用于存储最小元素的节点
// 遍历链表,寻找最小元素的前一个节点
while (p != NULL) {
if (p->data < q->next->data) {
// 更新q指针,指向当前节点,即最小元素的前一个节点
q = pre;
}
pre = p;
p = p->next;
}
// s指向最小元素节点
s = q->next;
// 将最小元素的前一个节点指向最小元素的后一个节点,实现删除操作
q->next = s->next;
// 释放最小元素节点的内存
delete s; // 使用delete而不是free
std::cout << "最小的元素是: " << s->data << std::endl;
}19、删除单链表中重复的元素,单链表是有序的。
// 删除链表中重复的元素
void del_repreat(LinkList &L){
// 定义三个指针,p 用于遍历链表,q 用于比较当前节点和下一个节点,s 用于指向被删除的节点
LinkList p = L; // p 指向链表的头节点
LinkList q = L->next; // q 指向头节点的下一个节点,即链表的第一个元素
LinkList s; // s 用于指向被删除的节点
// 遍历链表,直到 q 指向链表的末尾
while(q){
// 如果 p 指向的节点的值与 q 指向的节点的值相同
if(p->data == q->data){
// 将 s 指向 q,以便稍后释放内存
s = q;
// 移动 q 指针到下一个节点
q = q->next;
// 将 p 的 next 指向 q,从而跳过重复的节点
p->next = q;
// 释放 s 指向的节点的内存
free(s);
}else{
// 如果 p 和 q 的值不相同,移动 p 和 q 指针到下一个节点
p = p->next;
// 这里应该是 q = q->next; 否则会导致无限循环
q = p->next;
}
}
}20、找出两个链表 A 和 B 中相同的元素,并将这些相同的元素复制到一个新的链表 C 中 (A和B的元素分别是递增的)。
// 找出两个链表 A 和 B 中相同的元素,并将这些元素复制到链表 C 中
void find_repeat(LinkList &A, LinkList &B, LinkList &C) {
// 从 A 和 B 链表的第二个节点开始遍历(跳过头节点)
LinkList Ap = A->next;
LinkList Bp = B->next;
// 定义一个指针 cp,指向链表 C 的当前末尾节点
LinkList cp = C;
// 定义一个临时指针 s,用于创建新的节点
LinkList s;
// 遍历两个链表,直到任一链表到达末尾
while(Ap != NULL && Bp != NULL) {
if(Ap->data > Bp->data) {
// 如果 A 中的当前元素大于 B 中的当前元素,移动 B 的指针
Bp = Bp->next;
} else if(Ap->data < Bp->data) {
// 如果 A 中的当前元素小于 B 中的当前元素,移动 A 的指针
Ap = Ap->next;
} else {
// 如果两个元素相等,执行以下操作:
// 创建一个新的节点 s
s = new LinkNode;
// 将 A 中的当前元素的值复制到新节点 s 中
s->data = Ap->data;
// 将新节点 s 链接到链表 C 的末尾
cp->next = s;
// 设置新节点 s 的 next 指针为 NULL
s->next = NULL;
// 移动 cp 指针到链表 C 的新末尾
cp = s;
// 移动 A 和 B 的指针到下一个元素
Ap = Ap->next;
Bp = Bp->next;
}
}
// 确保链表 C 的末尾的 next 指针为 NULL
cp->next = NULL;
}代码中可能存在一些不足之处,仅供您参考。非常感谢您的宝贵意见和建议,以便我们能够不断改进和完善。