数据结构—单链表C语言刷题2

1.链表分割

2.链表的回文结构

3.相交链表

4.环形链表

5.环形链表II

1.链表分割

题目链接：链表分割

题目描述：现有一链表的头指针 ListNode* pHead，给一定值x，编写一段代码将所有小于x的结点排在其余结点之前，且不能改变原来的数据顺序，返回重新排列后的链表的头指针。

思路：另外定义两个链表，遍历原链表的每一个节点，将节点中存储数据比x小的节点尾插到链表1后，将节点中存储的数据比大于等于x的节点尾插到链表2后，循环完后再将链表2的头尾插到链表1，这样就将两个链表链接为一个新的链表，最后返回链表1的头节点

实现：另外开辟两个哨兵位的头节点，链表1的头节点指针为lessHead，链表2的头节点指针为greaterHead，然后再定义两个链表的尾指针用来尾插，链表1的尾为lessTail,链表2的尾为greadterTail；定义结构体指针cur从原链表的头head开始遍历链表，比较cur->val与x的大小关系：若cur->val小于x则将cur对应的节点插入到链表1后，也就是将lessTail->next指向cur，然后cur继续向后走一步，lessTail也向后走一步；若cur->val大于等于x则相同的方法将cur尾插到链表2后；cur走到NULL时原链表遍历完了，结束循环。之后将链表1链接到链表2后，这里需要注意：若倒数第二次循环判断的节点数据若大于等于x，则将该节点尾插到链表2后，greadterTail向后走一步之后指向该节点；最后一次循环判断的节点数据小于x，则将该节点尾插到链表2后，lessTail向后走一步指向该节点，然后循环结束了，greaterTail->next的值不会改变了，还是指向lessTail的，之后链接两个链表就会出现链表内成环的情况，链表2的尾节点指向链表1的尾结点，所以需要将greaterTail->next置成NULL。最后定义一个结构体指针list用来保存新链表的头指针，用来返回；动态开辟的两个哨兵位节点需要free掉

class Partition {
public:
    ListNode* partition(ListNode* pHead, int x) {
        struct ListNode* lessHead, *greaterHead, *lessTail, *greaterTail;
        lessHead = lessTail = (struct ListNode*)malloc(sizeof(struct ListNode));
        greaterHead  = greaterTail = (struct ListNode*)malloc(sizeof(struct ListNode));
         
        lessTail->next = greaterTail->next = NULL;
        struct ListNode* cur = pHead;
        while(cur)
        {
            if(cur->val < x)
            {
                lessTail->next = cur;
                lessTail = cur;
                cur = cur->next;
            }
            else
            {
                greaterTail->next = cur;
                greaterTail = cur;
                cur = cur->next;
            }
        }
        lessTail->next = greaterHead->next;
        greaterTail->next = NULL;  //避免新链表中出现环
        struct ListNode* list = lessHead->next;
        free(lessHead);
        free(greaterHead);
        lessHead = NULL;
        greaterHead = NULL;
        return list;
    }
};

2.链表的回文结构

题目链接：链表的回文结构

思路：先找到链表的中间节点，然后从中间节点处将之后的链表反转，再从链表的头节点和反转之后链表的中间节点开始比较两节点存储的数据，若不同则返回false，若相同则分别向后走继续判断；若循环结束了则返回true

实现：找链表的中间节点和反转链表在上一篇数据结构—单链表C语言刷题1中有题说明，这里直接引用这两个函数来实现相应的功能

/*
struct ListNode {
    int val;
    struct ListNode *next;
    ListNode(int x) : val(x), next(NULL) {}
};*/
//找到中间位置
struct ListNode* middleNode(struct ListNode* head)
{
    struct ListNode* slow = head;
    struct ListNode* fast = head;
    while(fast && fast->next)
    {
        slow = slow->next;
        fast = fast->next->next;
    }
    return slow;
}
 
//反转链表
struct ListNode* reverseList(struct ListNode* head)
{
    struct ListNode* cur = head;
    struct ListNode* newhead = NULL;
    while (cur)
    {
        struct ListNode* next = cur->next;
        cur->next = newhead;
        newhead = cur;
        cur = next;
    }
    return newhead;
}
 
class PalindromeList {
public:
    bool chkPalindrome(ListNode* A) {
        ListNode* mid = middleNode(A);//先找到中间位置
        struct ListNode* mid1 = reverseList(mid);//从中间位置反转链表
         
        //从头和从中间反转之后的链表依次比较
        while(A && mid1)
        {
            if(A->val != mid1->val)
            {
                return false;
            }
            A = A->next;
            mid1 = mid1->next;
        }
        return true;
    }
};

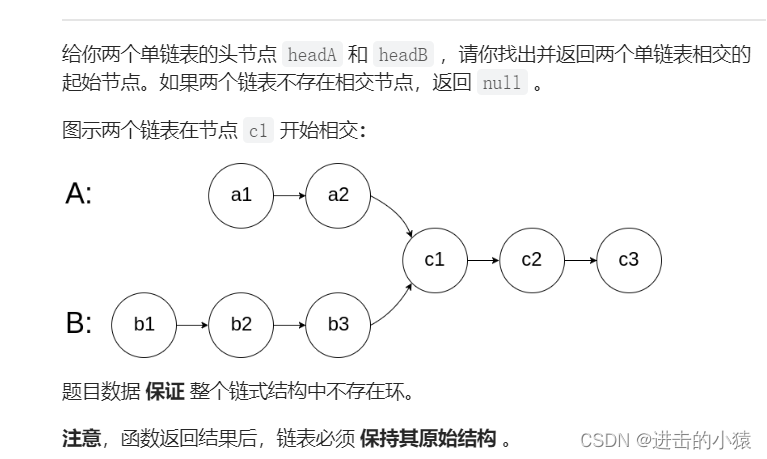
3.相交链表

链接：相交链表

描述：

实现思路：分别遍历A链表和B链表，找到两个链表的尾节点，比较尾节点数据是否相等，相等则两链表相交，不相等则返回NULL。遍历的同时记录两个链表的节点数，用于找相交节点；若判断相交之后让较长的链表先走两个链表节点数的差值步，之后再一块走，走到存储数据相同的节点就是要找的相交节点

struct ListNode* tailA = headA, *tailB = headB;
    int LenA = 1, LenB = 1;
    //分别遍历A,B，并分别记录节点数
    while(tailA->next)
    {
        LenA++;
        tailA = tailA->next;
    }
    while(tailB->next)
    {
        LenB++;
        tailB = tailB->next;
    }
    //A，B遍历完之后比较最后一个节点是否相等
    if(tailA != tailB)
    {
        return NULL;
    }
    struct ListNode* shortlist = headA, *longlist = headB;
    if(LenA > LenB)
    {
        shortlist = headB;
        longlist = headA;
    }
    int differ = abs(LenA - LenB);
    
    //长的链表先走它们的差值
    while(differ--)
    {
        longlist = longlist->next;
    }
    //在一起走，节点相同的位置就是交点
    while(longlist && shortlist)
    {
        if(longlist == shortlist)
        {
            return longlist;
        }
        longlist = longlist->next;
        shortlist = shortlist->next;
    }
    //这里要注意，虽然前面已经全部判断完了，一定会有一个返回值，但是最后还需要返回一个值，否则会有编译错误
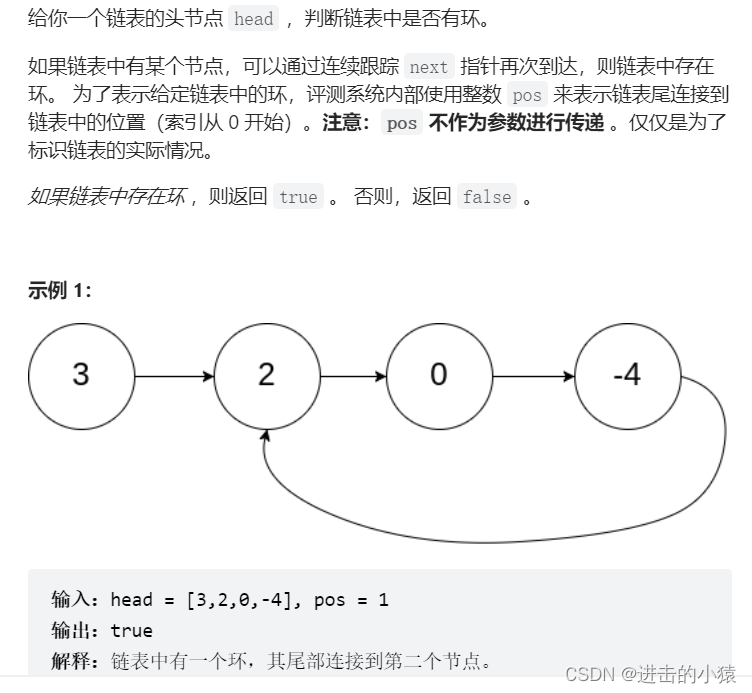
    return NULL;

4.环形链表

链接：环形链表

描述：

思路：快慢指针：定义两个结构体指针fast和slow，fast和slow同时从原链表的头开始向后走，fast每次走两步，slow每次走一步；若链表不存在环，则fast走到空或者fast->next为空循环结束，返回false；若链表存在环，则fast比slow每次走快一步，fast先进入环，slow后进去环，slow进入环之后，fast开始追slow，当追到的时候，也就是fast和slow指向同一个节点的时候，返回ture

bool hasCycle(struct ListNode *head) {
    struct ListNode* slow = head, *fast = head;
    while(fast && fast->next)
    {
        slow = slow->next;
        fast = fast->next->next;
        if(slow == fast)
        {
            return true;
        }
    }
    return false;
}

只有slow一次走一步，fast一次走两步时，才一定能追上。证明：fast走的快先进环，进环之后fast就在环里面走，当slow进环的时候，假设此时slow和fast相差为N个节点，则之后每循环一次，fast和slow就的距离就减小1，此过程如：N，N-1，N-2，...... ，1，0，当距离缩小为0的时候fast就追上slow了

slow一次走一步，fast一次三步时，不一定能追上。证明：fast走的快先进环，进环之后fast就在环里面走，当slow进环的时候，假设此时slow和fast相差为N个节点，则之后每循环一次，fast和slow就的距离就减小2，当N是偶数时，此过程变为：N，N-2，N-4，...... ，2，0，则能追上；当N是奇数时，此过程变为：N，N-2，N-4，...... ，1，-1设环的长度为C，则此时fast和slow之间的距离为C-1，若C-1为偶数则如上分析fast能追上slow，若C-1为奇数，则永远也追不上了

slow一次走一步，fast一次走四步/五步等等，也是不一定能追上，同理分析

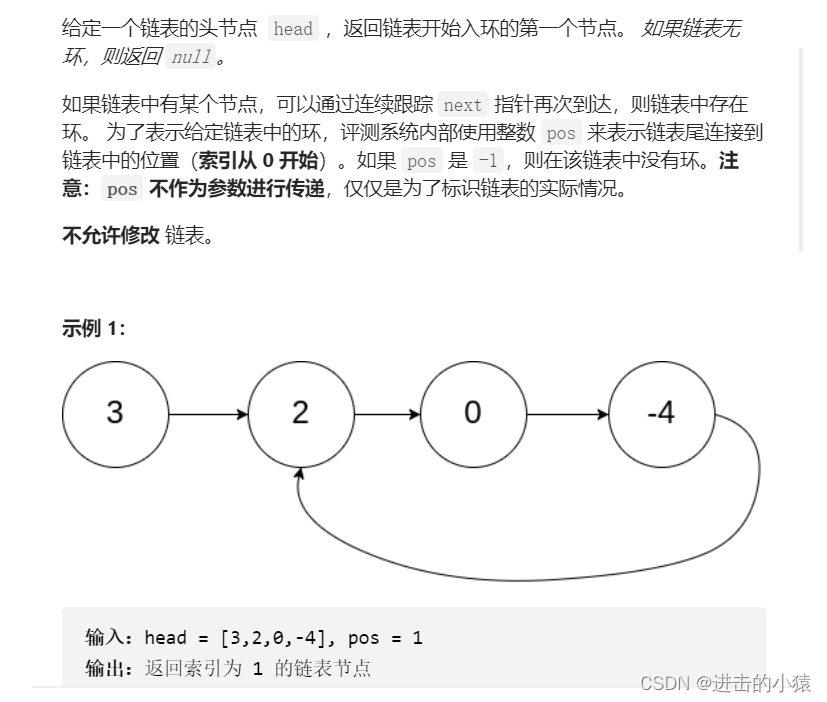
5.环形链表II

题目链接：环形链表II

描述：

这里的代码不是关键，而是需要证明一个关系公式。

设链表头到环入口点的距离为L，环入口点到fast与slow相交点的距离为X，环的长度为C；到fast与slow相遇点，slow走的距离为：L + X，fast走的距离为L + N*C + X，因为由于L和C大小差多少不确定，所以在slow进入环之前，fast可能走了很多圈也可能一圈也没走完，但是slow在进环之后的一圈内，fast一定能追上slow（slow进环之后fast和slow之间的距离最多为C-1）；又由于fast走的距离是slow的二倍，就有如下关系：2 *(L + X) = L + N*C + X，化简为：L = N*C - X，也可以写成：L = (N - 1)*C + (C - X)方便理解。公式意思为：fast和slow的相遇点到环入口点的距离与链表头到环入口点的距离相等

struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode* slow = head, *fast = head;
    while(fast && fast->next)
    {
        slow = slow->next;
        fast = fast->next->next;
        if(slow == fast)
        {
            struct ListNode* meet = slow;
            while(head != meet)
            {
                head = head->next;
                meet = meet->next;
            }
            return meet;
        }
    }
    return NULL;
}