系列文章戳这里👇
- 什么是上下文无关文法、最左推导和最右推导
- 如何判断二义文法及消除文法二义性
- 何时需要消除左递归
- 什么是句柄、什么是自上而下、自下而上分析
- 什么是LL(1)、LR(0)、LR(1)文法、LR分析表
- LR(0)、SLR(1)、LR(1)、LALR(1)文法之间的关系
- 编译原理第三章习题
- 词法分析、构建DFA、上下文无关文法、LL(1)分析、提取正规式
- 证明LL(1)、SLR(1)、LALR(1)文法
- 翻译方案、属性栈代码
- 【运行时环境】什么是活动记录、 活动记录与汇编代码的关系
编译原理—翻译方案、属性栈代码
文法如下:
S → ( L ) ∣ a L → L , S ∣ S S → (L) | a\\ L → L, S | S S→(L)∣aL→L,S∣S
(a) 写一个翻译方案,它输出每个 a 的嵌套深度。例如,对于句子 (a, (a, a)),输出的结果是 1 2 2。
文法符号S,L继承属性depth表示嵌套深度,则翻译方案如下:
S ′ → { S . d e p t h = 0 } S S → ( { L . d e p t h = S . d e p t h } L ) S → a { p r i n t ( S . d e p t h ) } L → { L 1 . d e p t h = L . d e p t h , S . d e p t h = L . d e p t h } L 1 , S L → { S . d e p t h = L . d e p t h } S \begin{aligned} S'&→\{S.depth=0\}S\\ S&→(\{L.depth = S.depth\}L)\\ S&→a\{print(S.depth)\}\\ L&→\{L_1.depth=L.depth,S.depth=L.depth\}L_1,S\\ L&→\{S.depth=L.depth\}S \end{aligned} S′SSLL→{S.depth=0}S→({L.depth=S.depth}L)→a{print(S.depth)}→{L1.depth=L.depth,S.depth=L.depth}L1,S→{S.depth=L.depth}S
属性栈代码,由于 属性栈上仅能存放综合属性(后文有详细介绍),所以需要引入标记非终结符P、Q、R,及其综合属性s,继承属性i,模拟继承属性的计算,则栈代码如下:
S ′ → { S . d e p t h = P . s } P S P → ϵ { P . s = 0 } S t a c k [ n t o p ] = 0 S → ( { Q . i = S . d e p t h , L . d e p t h = Q . s } Q L ) Q → ϵ { Q . s = Q . i + 1 } S t a c k [ n t o p ] = S t a c k [ t o p − 1 ] + 1 S → a { p r i n t ( S . d e p t h ) } p r i n t ( S t a c k [ t o p − 1 ] ) L → { L 1 . d e p t h = L . d e p t h , R . i = L . d e p t h , S . d e p t h = R . s } L 1 , R S R → ϵ { R . s = R . i } S t a c k [ n t o p ] = S t a c k [ t o p − 2 ] L → { S . d e p t h = L . d e p t h } S \begin{aligned} S'&→\{S.depth=P.s\}PS\\ P&→\epsilon\{P.s=0\}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Stack[ntop]=0\\ S&→(\{Q.i=S.depth,L.depth = Q.s\}QL)\\ Q&→\epsilon\{Q.s=Q.i+1\}\ \ \ \ \ \ \ \ \ \ \ \ Stack[ntop]= Stack[top-1]+1\\ S&→a\{print(S.depth)\}\ \ \ \ \ \ \ \ \ \ print(Stack[top-1])\\ L&→\{L_1.depth=L.depth,R.i=L.depth,S.depth=R.s\}L_1,RS\\ R&→\epsilon\{R.s=R.i\}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Stack[ntop] = Stack[top-2]\\ L&→\{S.depth=L.depth\}S \end{aligned} S′PSQSLRL→{S.depth=P.s}PS→ϵ{P.s=0} Stack[ntop]=0→({Q.i=S.depth,L.depth=Q.s}QL)→ϵ{Q.s=Q.i+1} Stack[ntop]=Stack[top−1]+1→a{print(S.depth)} print(Stack[top−1])→{L1.depth=L.depth,R.i=L.depth,S.depth=R.s}L1,RS→ϵ{R.s=R.i} Stack[ntop]=Stack[top−2]→{S.depth=L.depth}S
(b) 写一个翻译方案,它打印出每个 a 在句子中是第几个字符。例如,当句子是 (a, (a, (a, a),(a)))时,打印的结果是 2 5 8 10 14。
使用综合属性out表示当前文法符号推出的字符总数,基础属性before表示该文法符号前有多少个字符,则翻译方案如下:
S
′
→
{
S
.
b
e
f
o
r
e
=
0
}
S
S
→
{
L
.
b
e
f
o
r
e
=
S
.
b
e
f
o
r
e
}
(
L
)
{
S
.
o
u
t
=
L
.
o
u
t
+
2
}
S
→
a
{
S
.
o
u
t
=
1
;
p
r
i
n
t
(
S
.
b
e
f
o
r
e
+
1
)
}
L
→
{
L
1
.
b
e
f
o
r
e
=
L
.
b
e
f
o
r
e
,
S
.
b
e
f
o
r
e
=
L
.
b
e
f
o
r
e
+
L
1
.
o
u
t
+
1
}
L
1
,
S
{
L
.
o
u
t
=
L
1
.
o
u
t
+
S
.
o
u
t
+
1
}
L
→
{
S
.
b
e
f
o
r
e
=
L
.
b
e
f
o
r
e
}
S
{
L
.
o
u
t
=
S
.
o
u
t
}
\begin{aligned} S'&→\{S.before=0\}S\\ S&→\{L.before = S.before\} \\&\ \ \ \ \ \ \ \ \ \ \ (L) \\&\ \ \ \ \ \ \ \ \ \ \ \{S.out=L.out+2\}\\ S&→a\{S.out=1;print(S.before+1)\}\\ L&→\{L_1.before=L.before, \\&\ \ \ \ \ \ \ \ \ \ \ S.before=L.before+L_1.out+1\} \\&\ \ \ \ \ \ \ \ \ \ \ L_1,S \\&\ \ \ \ \ \ \ \ \ \ \ \{L.out=L_1.out+S.out+1\}\\ L&→\{S.before=L.before\}S\{L.out=S.out\} \end{aligned}
S′SSLL→{S.before=0}S→{L.before=S.before} (L) {S.out=L.out+2}→a{S.out=1;print(S.before+1)}→{L1.before=L.before, S.before=L.before+L1.out+1} L1,S {L.out=L1.out+S.out+1}→{S.before=L.before}S{L.out=S.out}
同理,引入标记非终结符P、Q、R,及其综合属性s,继承属性i,模拟继承属性的计算,上述翻译方案栈代码如下:
S
′
→
{
S
.
b
e
f
o
r
e
=
P
.
s
}
P
S
P
→
ϵ
{
P
.
s
=
0
}
S
t
a
c
k
[
n
t
o
p
]
=
0
S
→
(
{
Q
.
i
=
S
.
b
e
f
o
r
e
,
L
.
b
e
f
o
r
e
=
Q
.
s
}
Q
L
)
{
S
.
o
u
t
=
L
.
o
u
t
+
2
}
Q
→
ϵ
{
Q
.
s
=
Q
.
i
+
1
}
S
t
a
c
k
[
n
t
o
p
]
=
S
t
a
c
k
[
t
o
p
−
1
]
+
1
S
→
a
{
p
r
i
n
t
(
S
.
b
e
f
o
r
e
)
}
p
r
i
n
t
(
S
t
a
c
k
[
t
o
p
−
1
]
)
L
→
{
L
1
.
b
e
f
o
r
e
=
L
.
b
e
f
o
r
e
,
R
.
i
=
L
.
b
e
f
o
r
e
+
L
1
.
o
u
t
+
1
,
S
.
b
e
f
o
r
e
=
R
.
s
}
L
1
,
R
S
{
L
.
o
u
t
=
L
1
.
o
u
t
+
S
.
o
u
t
+
1
}
S
t
a
c
k
[
n
t
o
p
]
=
S
t
a
c
k
[
t
o
p
−
3
]
+
S
t
a
c
k
[
t
o
p
]
+
1
R
→
ϵ
{
R
.
s
=
R
.
i
}
S
t
a
c
k
[
n
t
o
p
]
=
S
t
a
c
k
[
t
o
p
−
2
]
+
S
t
a
c
k
[
t
o
p
−
1
]
+
1
L
→
{
S
.
b
e
f
o
r
e
=
L
.
b
e
f
o
r
e
}
S
{
L
.
o
u
t
=
S
.
o
u
t
}
S
t
a
c
k
[
n
t
o
p
]
=
S
t
a
c
k
[
t
o
p
]
\begin{aligned} S'&→\{S.before=P.s\}PS\\ P&→\epsilon\{P.s=0\}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Stack[ntop]=0\\ S&→(\{Q.i = S.before,L.before = Q.s\} \\&\ \ \ \ \ \ \ \ \ \ \ QL) \\&\ \ \ \ \ \ \ \ \ \ \ \{S.out=L.out+2\} \\ Q&→\epsilon\{Q.s=Q.i+1\}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Stack[ntop]= Stack[top-1]+1\\ S&→a\{print(S.before)\}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ print(Stack[top-1])\\ L&→\{L_1.before=L.before, \\&\ \ \ \ \ \ \ \ \ \ \ R.i=L.before+L_1.out+1, \\&\ \ \ \ \ \ \ \ \ \ \ S.before=R.s\} \\&\ \ \ \ \ \ \ \ \ \ \ L_1,RS \\&\ \ \ \ \ \ \ \ \ \ \ \{L.out=L_1.out+S.out+1\} \ \ \ \ \ \ \ \ \ Stack[ntop]=Stack[top-3]+Stack[top]+1 \\ R&→\epsilon\{R.s=R.i\}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Stack[ntop] = Stack[top-2]+Stack[top-1]+1\\ L&→\{S.before=L.before\}S \\& \ \ \ \ \ \ \ \{L.out=S.out\} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Stack[ntop]=Stack[top] \end{aligned}
S′PSQSLRL→{S.before=P.s}PS→ϵ{P.s=0} Stack[ntop]=0→({Q.i=S.before,L.before=Q.s} QL) {S.out=L.out+2}→ϵ{Q.s=Q.i+1} Stack[ntop]=Stack[top−1]+1→a{print(S.before)} print(Stack[top−1])→{L1.before=L.before, R.i=L.before+L1.out+1, S.before=R.s} L1,RS {L.out=L1.out+S.out+1} Stack[ntop]=Stack[top−3]+Stack[top]+1→ϵ{R.s=R.i} Stack[ntop]=Stack[top−2]+Stack[top−1]+1→{S.before=L.before}S {L.out=S.out} Stack[ntop]=Stack[top]
针对以下文法
E
→
E
’
>
’
E
∣
E
’
<
’
E
∣
n
u
m
b
e
r
E → E ’>’ E\\ \ \ \ \ \ \ \ \ \ \ | E ’<’ E\\ \ \ \ \ \ \ \ \ \ \ | number
E→E’>’E ∣E’<’E ∣number
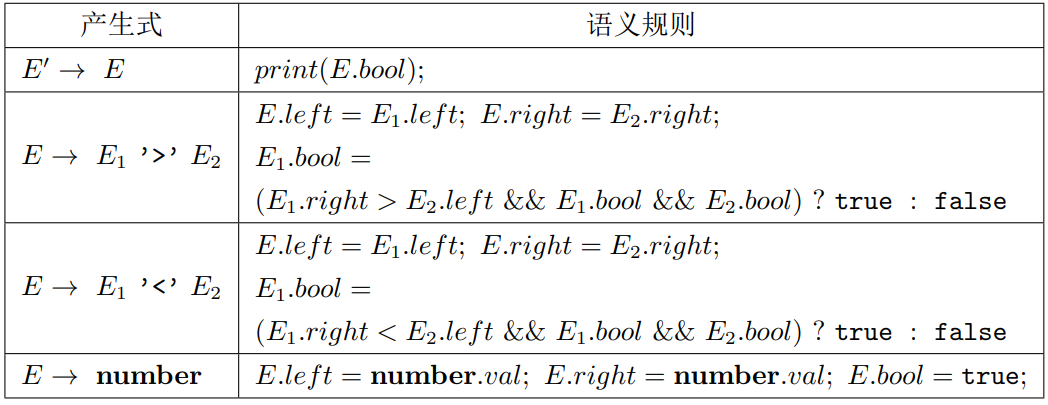
(c)设计语法制导定义,使之能计算诸如 1 < 2 < 3 的表达式值为 True;而计算表达式 1 < 5 >
3 的值也为 True。
用综合属性 lef t 和 right 表示 E 推出的字符序列中最左和最右的数字,综合属性 bool 表
示 E 推出的表达式的布尔值,语法制导的定义如下:
(d) 给出生成如下 C 风格for语句中间代码的翻译方案;假定代码生成的顺序不变。
S
→
f
o
r
(
E
1
;
E
2
;
E
3
)
S
1
S → for(E1; E2; E3) S1
S→for(E1;E2;E3)S1
首先给出中间代码的结构
据此给出一个翻译方案如下
属性栈代码:
- 如何在自底向上分析中计算继承属性?
- 属性栈上仅能存放综合属性
- 分析栈中符号的继承属性
- 属性copy规则
如果, A → X Y A→XY A→XY,有语义规则 Y . i : = X . s Y.i := X.s Y.i:=X.s,
翻译方案可写为:
A → X { Y . i : = X . s } Y A → X \{ Y.i := X.s \} Y A→X{Y.i:=X.s}Y
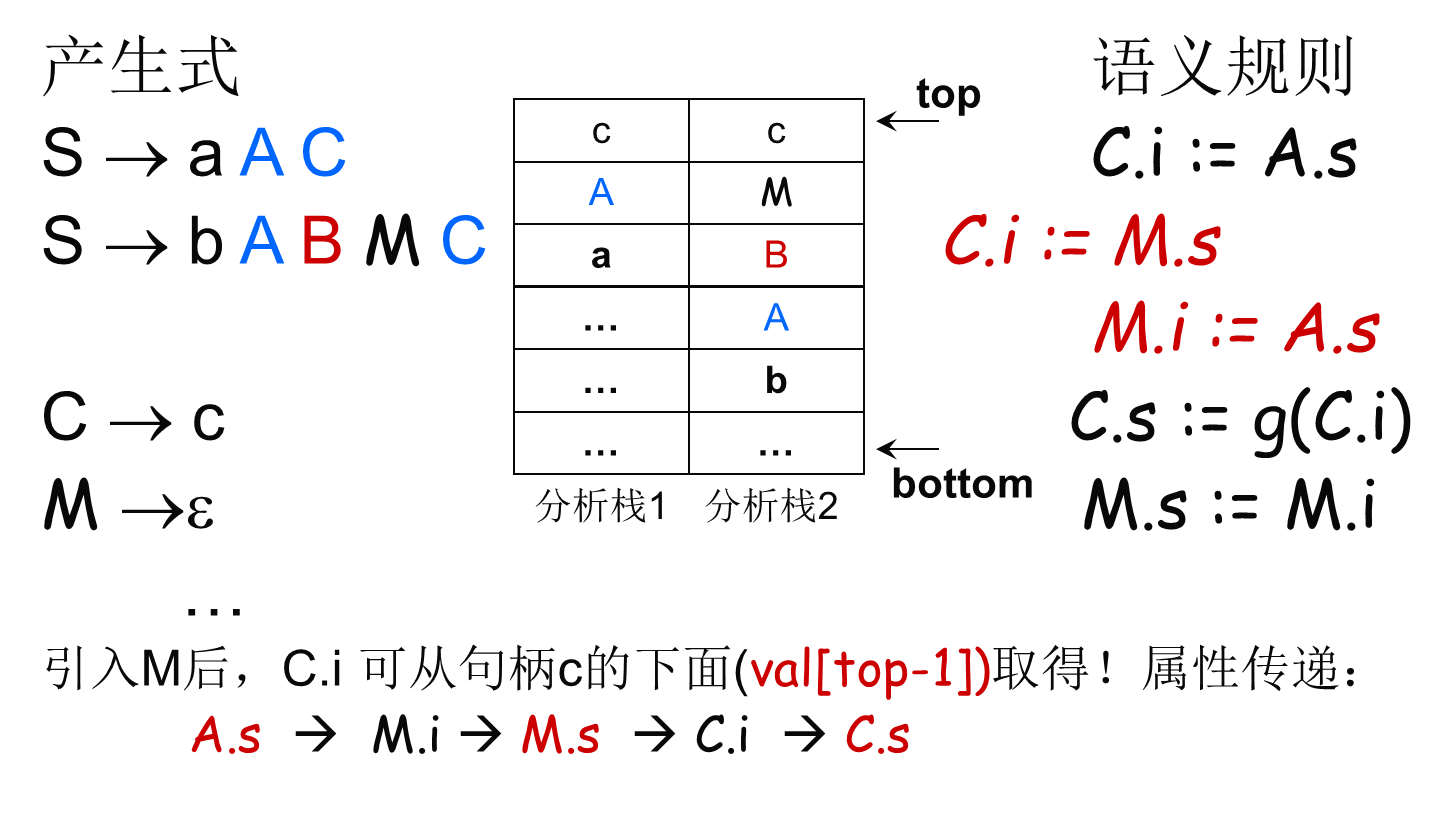
- 属性copy规则
- 从句柄下面取继承属性!
举个栗子
有如下文法与翻译方案
D→T { L.in := T.type } L
T→int { T.type := integer }
T→real { T.type := real }
L→ { L1.in := L.in }
L1 , id {addtype(id.entry, L.in) }
L→id { addtype(id.entry, L.in) }
对于输入串:int p,q,r 分析过程如下:
引入标记非终结符模拟继承属性的计算