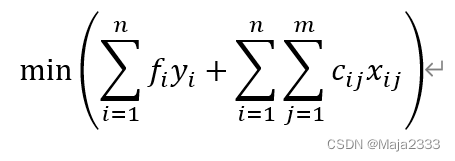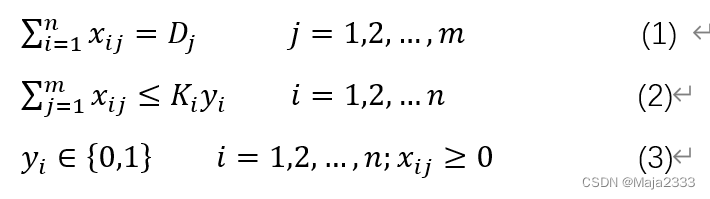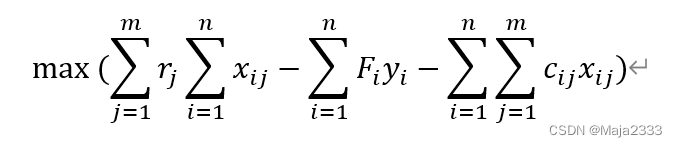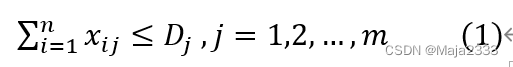Bootstrap

补充1 设计区域网络配置的优化模型(工厂选址模型)——基于java和cplex的实现

这一部分是第二部分的供应链网络的设计(二)供应链的网络设计第四部分设计区域网络配置的优化模型。

目录

一、所需输入

二、有能力约束的工厂选址模型

1.利用excel进行规划求解

2.利用java和cplex进行规划求解

三、考虑税收、关税和顾客要求

一、所需输入

        使用网络优化模型来进行区域网络配置时，管理者需要获得各个区域的以下信息：需求、期望的响应水平、兴建设施的固定成本、劳动力和材料的变动成本、库存持有成本、每两个地区之间的运输成本、产品售价、税收和关税、设施产能。结合这些成本及税收和关税信息，就可以了解在每个地区兴建设施的年固定成本，以及从一个地区到另一个地区提供单位产品的可变成本。

        MoonLight公司是一家经营不锈钢制造的公司，其产品销往全球各个地方。接下来，就借MoonLight公司为例说明区域网络的设计。假如你是该公司负责供应链的副总裁，当前有两种备选方案，你会选择哪一种方案呢？

        第一种方案是在每个地区都兴建一个工厂。这种方案的好处是可以降低运输成本，而且有助于避免从其他地区进口产品可能被征收的关税。这种方案的缺点是工厂的规模是按满足当地需求来规划的，有可能无法充分利用规模经济。

        第二种方案将工厂集中建在少数几个地区，这样可以提高规模经济水平，但会增加运输成本和关税。

        作为总裁的你，必须同时你还要考虑对这些可量化因素进行权衡，同时还必须考虑竞争环境、政治风险等一些不可量化的因素。面对这样的方案选择，当然不能拍脑袋就决定，必须进行一番细致的考察和计算，接下来就正式开始介绍工厂选址模型。

        

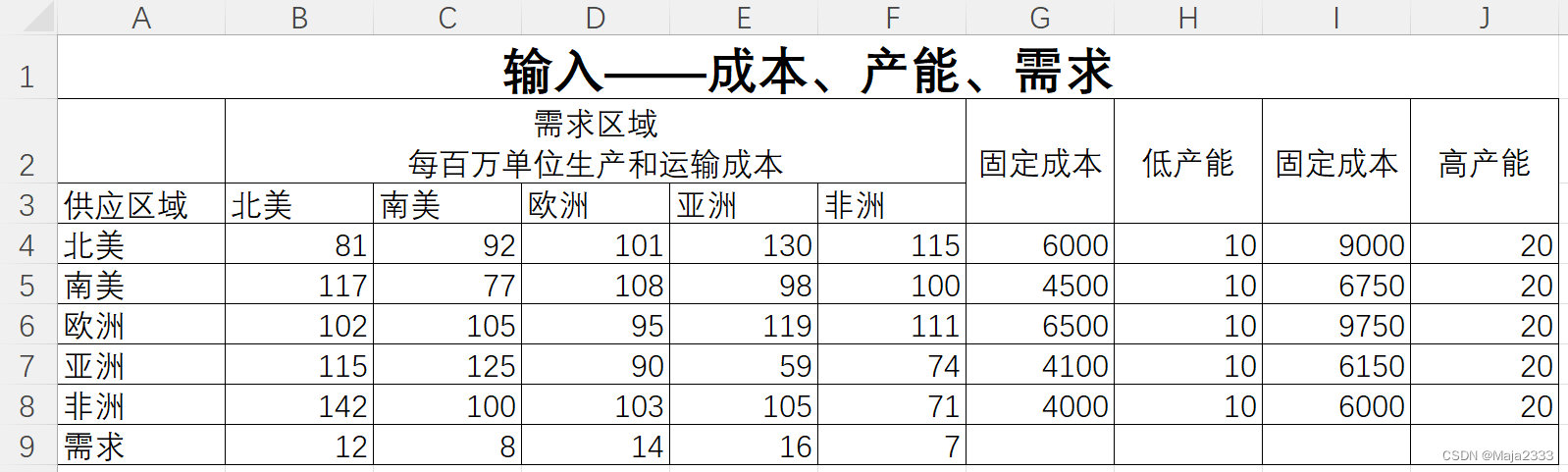
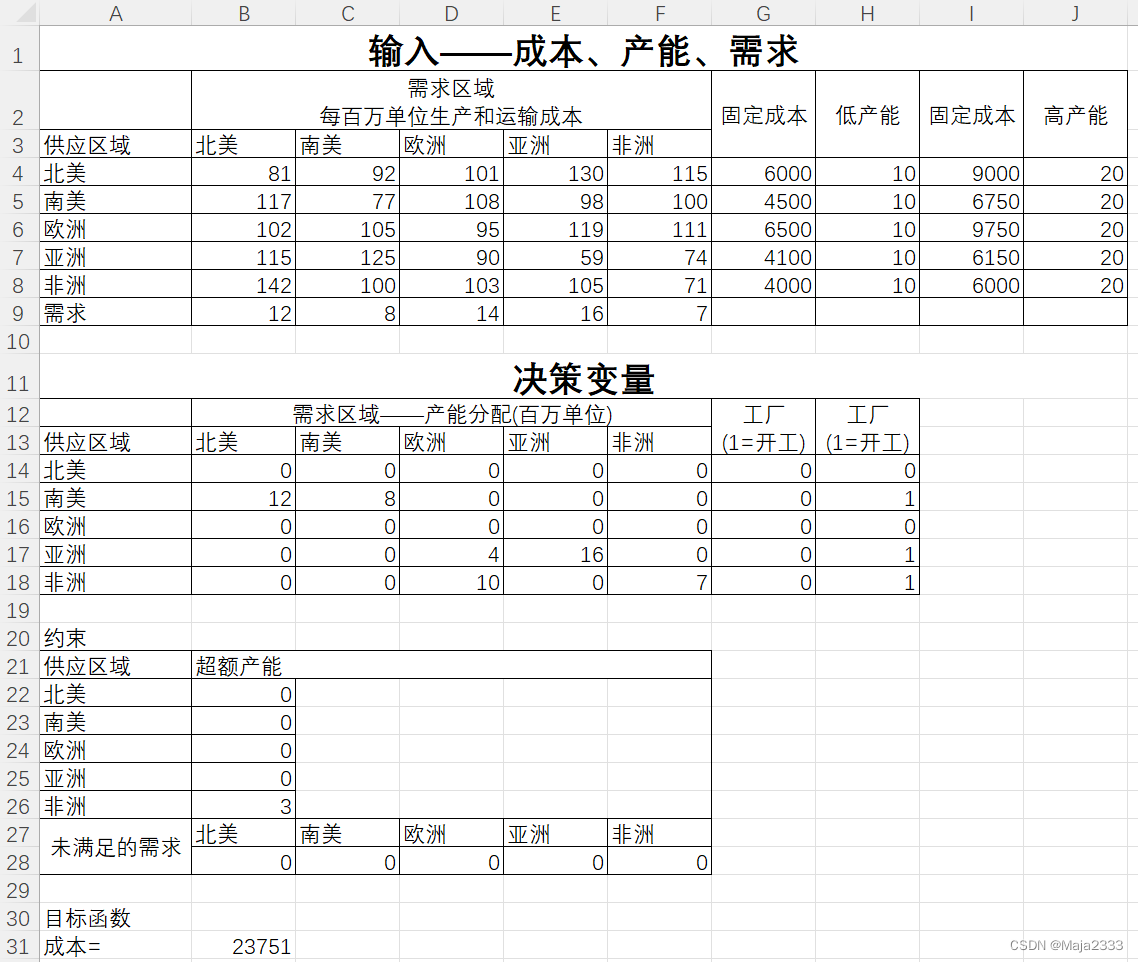
         第一步是收集可用于量化模型的数据。对于MoonLight公司来说，你决定要全球需求划分为5个区域：北美、南美、欧洲、非洲和亚洲。所收集的数据如下图所示。上述几个区域的年需求都在B9 ：F9中。单元格B4：F8中的数据标识在一个区域组织生产来满足另一个区域需求的可变生产、库存和运输成本（包括关税和税收）。所有成本都是以千美元为单位。这个阶段收集的数据是一个总量数据。

MoonLight公司的成本(以千美元计)和需求数据(以百万单位计) 

        在每个设施，与设施、运输和库存相关的成本既有固定成本也有可变成本。设施、运输和库存成本通常存在规模经济效应，边际成本随着设施生产数量的增加而降低。在这里讨论时，我们假定所有的可变成本与生产量或运输量程线性正相关。

        MoonLight公司对于每个选址的工厂规模也有两个方案。低产能的工厂每年生产1000万单位产品，高产能工厂每年可生产2000万单位产品，分别如单元格H4：H8和J4：J8所示。由于高产能工厂具有一定的规模经济，所以其固定成本不到低产能工厂固定成本的两倍，如单元格G4：G8和I4:I8所示。所有的固定成本都按年计算。你想知道哪种网络方案的成本最低。为了回答这个问题接下来将要讨论这种情况的、有能力约束的工厂选址模型。

二、有能力约束的工厂选址模型

        有能力约束的工厂选址网络优化模型需要以下输入：

        在MoonLight公司的例子中，n=10，因为有5个潜在工厂位置和2种可供选择的工厂产能。m=5，因为有5个市场。年需求Dj见B9:F9单元格。工厂潜在产能Ki见单元格H4:H8和J4:J8。单元格G4:G8和I4:I8中数据标识年固定成本fi。变动成本cij如表格B4:F8所示。

        供应链小组的目标时确定一个可以使税后利润最大化的网络设计。为了简化起见，假设所有需求都必须被满足且不考虑所得税。因此，模型仅关注使满足全球需求的成本最小化。不过，也可以对模型稍加修改，将利润和税收纳入考虑之中。相关决策变量定义如下： 

     

         则问题可以表述为以下混合整数规划问题：

        约束条件为：

         目标函数是使简历和运营该网络的总成本(固定成本+可变成本)最小化。式(1)的约束条件是指每个区域的市场需求都必须被满足。式(2)的约束条件是指每个工厂的供应不能超出其产能。式(3)的约束条件是指一个工厂或是开工，或是关闭。函数的姐将表明哪些工厂将开工及其产能，以及各区域的需求在这些工厂之间如何分配。

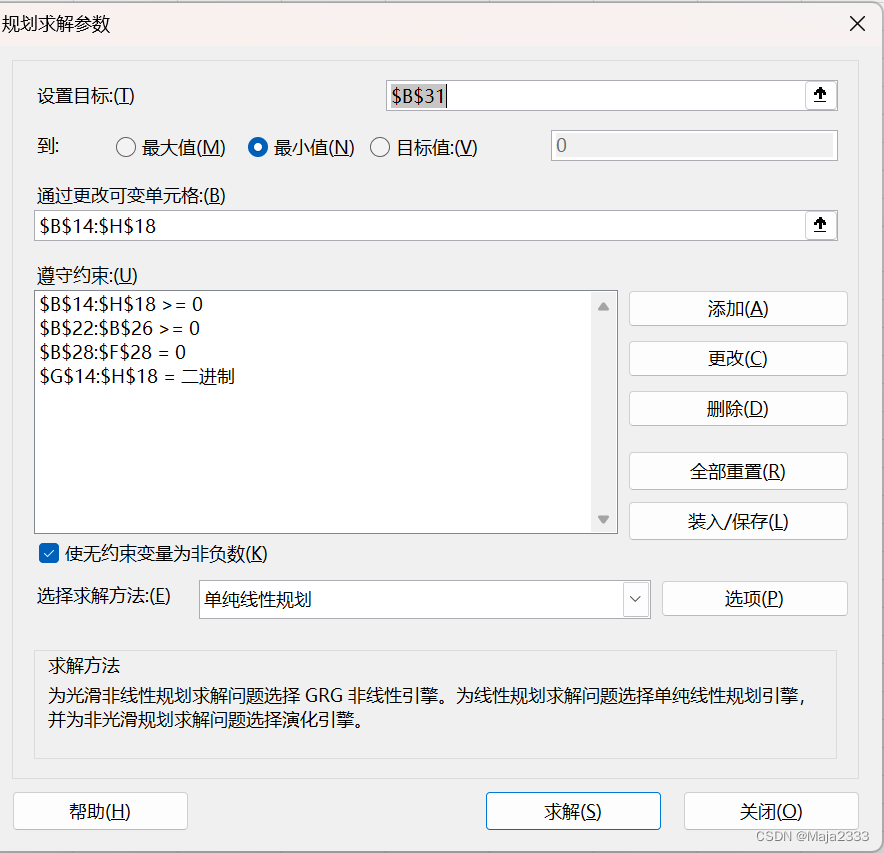
1.利用excel进行规划求解

        该模型可利用Excel中的规划求解工具来进行求解。由于篇幅原因，这部分内容不过介绍，有兴趣的朋友可以自己上网查询。

        

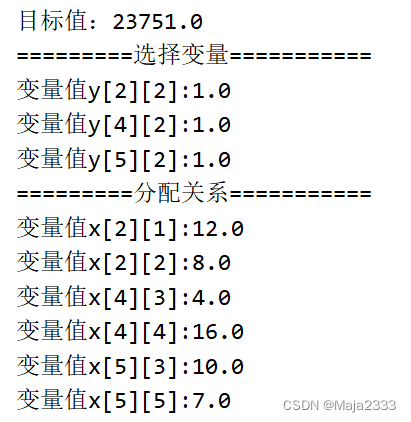
         上图便是EXCEL得到的结果，分别在南美、亚洲和非洲建设一个高产能的工厂。南美的工厂满足北美的需求。欧洲的需求由亚洲和非洲的工厂来满足。这种方案下，最低成本为23751千美元。

2.利用java和cplex进行规划求解

       Cplex是IBM公司开发的一款商业版的优化引擎，该引擎专门用于求解大规模的线性规划（LP）、二次规划（QP）、带约束的二次规划（QCQP）、二阶锥规划（SOCP）等四类基本问题，以及相应的混合整数规划（MIP）问题，并且与众多优化软件及语言兼容（与C++，JAVA，EXCEL，Matlab等都有接口）。

        java引入cplex在这不多讲述了，不了解的直接在论坛里搜就可以了，废话不多说，直接上代码。

public class InputData {
    //产品需求
    double[] demands={12,8,14,16,7};
    //低产能固定成本
    double[] lowFixedCost={6000,4500,6500,4100,4000};
    //高产能固定成本
    double[] highFixedCost={9000,6750,9750,6150,6000};
    //低产能
    double[] lowProductivity = {10,10,10,10,10};
    //高产能
    double[] highProductivity = {20,20,20,20,20};
    //成本
    double[][] cost = {
            {81,92,101,130,115},
            {117,77,108,98,100},
            {102,105,95,119,111},
            {115,125,90,59,74},
            {142,100,103,105,71}
    };
    int nodeNumber = demands.length;
}

import ilog.concert.IloException;
import ilog.concert.IloNumExpr;
import ilog.concert.IloNumVar;
import ilog.concert.IloNumVarType;
import ilog.cplex.IloCplex;

public class LocationDemo {
    InputData data;

    public LocationDemo(InputData data) {
        this.data = data;
    }

    //定义cplex内部对象
    IloCplex model;
    //定义变量
    public IloNumVar[][] y;
    public IloNumVar[][] x;

    //求解函数
    public void solve() throws IloException{
        if(model.solve()==false){
            System.out.println("模型不可解");
        } else {
            System.out.println(model);
            System.out.println("目标值："+model.getObjValue());
            System.out.println("=========选择变量===========");
            for(int i=0;i<data.nodeNumber;i++){
                for(int j=0;j<2;j++) {
                    if (model.getValue(y[i][j]) != 0) {
                        System.out.println("变量值y[" + (i + 1) + "]["+(j+1)+"]:" + model.getValue(y[i][j]));
                    }
                }
            }
            System.out.println("=========分配关系===========");
            for(int i=0;i<data.nodeNumber;i++){
                for(int j=0;j<data.nodeNumber;j++) {
                    if (model.getValue(x[i][j]) != 0) {
                        System.out.println("变量值x[" + (i + 1) + "]["+(j+1)+"]:" + model.getValue(x[i][j]));
                    }
                }
            }
        }
    }

    //根据数学模型建立求解模型
    public void BuildModel() throws IloException{
        //初始化model
        model = new IloCplex();
        model.setOut(null);
        //定义决策变量x和y的数据类型及取值范围
        y = new IloNumVar[data.nodeNumber][2];
        x = new IloNumVar[data.nodeNumber][data.nodeNumber];
        for (int i = 0; i < data.nodeNumber; i++) {
            for(int j=0;j<data.nodeNumber;j++) {
                x[i][j] = model.numVar(0,20, IloNumVarType.Int, "x[" + i + "]["+j+"]");
            }
        }
        for (int i = 0; i < data.nodeNumber; i++) {
            for(int j=0;j<2;j++) {
                y[i][j] = model.numVar(0,1, IloNumVarType.Bool, "y[" + i + "]["+j+"]");
            }
        }
        //设置目标函数
        IloNumExpr obj = model.numExpr();
        for(int i=0;i<data.nodeNumber;i++){
            for (int j = 0; j < data.nodeNumber; j++) {
                obj = model.sum(obj,model.prod(data.cost[i][j],x[i][j]));
            }
        }
        for (int i = 0; i < data.nodeNumber; i++) {
            obj = model.sum(obj,model.prod(data.lowFixedCost[i],y[i][0]));
        }
        for (int i = 0; i < data.nodeNumber; i++) {
            obj = model.sum(obj,model.prod(data.highFixedCost[i],y[i][1]));
        }
        model.addMinimize(obj);
        //设置约束条件1
        for(int j=0;j<data.nodeNumber;j++) {
            IloNumExpr expr1 = model.numExpr();
            for (int i = 0; i < data.nodeNumber; i++) {
                expr1 = model.sum(expr1, x[i][j]);
            }
            model.addEq(expr1,data.demands[j]);
        }
        //设置约束条件2
        for (int i = 0; i < data.nodeNumber; i++) {
            IloNumExpr expr2 = model.numExpr();
            for(int j=0;j<data.nodeNumber;j++){
                expr2=model.sum(expr2,x[i][j]);
            }
            model.addLe(expr2,model.sum(model.prod(y[i][0],data.lowProductivity[i]),model.prod(y[i][1],data.highProductivity[i])));
        }

    }
}

public class test {
    public static void main(String[] args) throws Exception {
        InputData data =new InputData();
        LocationDemo lp=new LocationDemo(data);
        lp.BuildModel();
        lp.solve();
    }
}

结果和excel运行结果相同，下图为运行结果：

 

三、考虑税收、关税和顾客要求

        所有网络设计模型的构建应确保最终的供应链网络在满足顾客服务要求的同时，实现税后利润最大化。以下所介绍的方法可用于将任何成本最小化的网络设计模型转换为利润最大化模型。如果rj是在市场j卖出一单位产品的收入，则有能力约束的工厂选址模型的目标函数可以修改为：

该目标函数是使企业的利润最大化。当使用一个利润最大化的目标函数时，管理者应当将上面的(1)式修改为：

        上面的约束条件更为适合，因为它允许网络设计者识别处哪些需求可以获利，而满足哪些需求会使企业造成损失，用上面的式子为利润最大化的工厂选址模型将进服务于能够获利的那部分需求。除非有其他约束条件，否则这可能导致一些市场中的部分需求被放弃。因为服务这些需求企业无利可图。下面是改进后的java代码。

public class ImproveData {
    //产品需求
    double[] demands={12,8,14,16,7};
    //低产能固定成本
    double[] lowFixedCost={6000,4500,6500,4100,4000};
    //高产能固定成本
    double[] highFixedCost={9000,6750,9750,6150,6000};
    //低产能
    double[] lowProductivity = {10,10,10,10,10};
    //高产能
    double[] highProductivity = {20,20,20,20,20};
    //成本
    double[][] cost = {
            {81,92,101,130,115},
            {117,77,108,98,100},
            {102,105,95,119,111},
            {115,125,90,59,74},
            {142,100,103,105,71}
    };
    //单位产品的收入
    double[] income = {550,525,555,530,520};
    int nodeNumber = demands.length;
}

import ilog.concert.IloException;
import ilog.concert.IloNumExpr;
import ilog.concert.IloNumVar;
import ilog.concert.IloNumVarType;
import ilog.cplex.IloCplex;

public class ImproveDemo {
    ImproveData data;

    public ImproveDemo(ImproveData data) {
        this.data = data;
    }

    //定义cplex内部对象
    IloCplex model;
    //定义变量
    public IloNumVar[][] y;
    public IloNumVar[][] x;

    //求解函数
    public void solve() throws IloException{
        if(model.solve()==false){
            System.out.println("模型不可解");
        } else {
            System.out.println(model);
            System.out.println("目标值："+model.getObjValue());
            System.out.println("=========选择变量===========");
            for(int i=0;i<data.nodeNumber;i++){
                for(int j=0;j<2;j++) {
                    if (model.getValue(y[i][j]) != 0) {
                        System.out.println("变量值y[" + (i + 1) + "]["+(j+1)+"]:" + model.getValue(y[i][j]));
                    }
                }
            }
            System.out.println("=========分配关系===========");
            for(int i=0;i<data.nodeNumber;i++){
                for(int j=0;j<data.nodeNumber;j++) {
                    if (model.getValue(x[i][j]) != 0) {
                        System.out.println("变量值x[" + (i + 1) + "]["+(j+1)+"]:" + model.getValue(x[i][j]));
                    }
                }
            }
        }
    }

    //根据数学模型建立求解模型
    public void BuildModel() throws IloException{
        //初始化model
        model = new IloCplex();
        model.setOut(null);
        //定义决策变量x和y的数据类型及取值范围
        y = new IloNumVar[data.nodeNumber][2];
        x = new IloNumVar[data.nodeNumber][data.nodeNumber];
        for (int i = 0; i < data.nodeNumber; i++) {
            for(int j=0;j<data.nodeNumber;j++) {
                x[i][j] = model.numVar(0,20, IloNumVarType.Int, "x[" + i + "]["+j+"]");
            }
        }
        for (int i = 0; i < data.nodeNumber; i++) {
            for(int j=0;j<2;j++) {
                y[i][j] = model.numVar(0,1, IloNumVarType.Bool, "y[" + i + "]["+j+"]");
            }
        }
        //修改后的目标函数
        IloNumExpr obj = model.numExpr();
        for (int i = 0; i < data.nodeNumber; i++) {
            for (int j = 0; j < data.nodeNumber; j++) {
                obj = model.sum(obj,model.prod(data.income[i],x[j][i]));
            }
        }
        for(int i=0;i<data.nodeNumber;i++){
            for (int j = 0; j < data.nodeNumber; j++) {
                obj = model.diff(obj,model.prod(data.cost[i][j],x[i][j]));
            }
        }
        for (int i = 0; i < data.nodeNumber; i++) {
            obj = model.diff(obj,model.prod(data.lowFixedCost[i],y[i][0]));
        }
        for (int i = 0; i < data.nodeNumber; i++) {
            obj = model.diff(obj,model.prod(data.highFixedCost[i],y[i][1]));
        }
        model.addMaximize(obj);
        //修改后的设置约束条件1
        for(int j=0;j<data.nodeNumber;j++) {
            IloNumExpr expr1 = model.numExpr();
            for (int i = 0; i < data.nodeNumber; i++) {
                expr1 = model.sum(expr1, x[i][j]);
            }
            model.addLe(expr1,data.demands[j]);
        }
        //设置约束条件2
        for (int i = 0; i < data.nodeNumber; i++) {
            IloNumExpr expr2 = model.numExpr();
            for(int j=0;j<data.nodeNumber;j++){
                expr2=model.sum(expr2,x[i][j]);
            }
            model.addLe(expr2,model.sum(model.prod(y[i][0],data.lowProductivity[i]),model.prod(y[i][1],data.highProductivity[i])));
        }

    }
}
public class test {
    public static void main(String[] args) throws Exception {
        ImproveData data =new ImproveData();
        ImproveDemo lp=new ImproveDemo(data);
        lp.BuildModel();
        lp.solve();
    }
}

 运行结果：

         顾客的偏好和要求可以通过期望的响应时间、对运输方式或运输承运人的选择等方式表现出来。例如，假设在工厂选址i和市场j之间存在两种运输方式：方式1是海运，方式2是空运。那么，可以对工厂选址模型做以下修正：定义两个独立的决策变量x1ij和x2ij，分别标识采用方式1和方式2从选址i运送到市场j的数量。只有当使用某种运输方式所花费的时间小于所期望的响应时间时，才允许利用这种运输方式进行装运。例如，如果采用方式1(海运)从地址i运送产品到市场j所需时间大于顾客所能接受的时间，那么可以在工厂选址模型中将决策变量x1ij赋值为0。存在多个运输承运人是可以对模型做类似修改。改进的代码就不放在这里了。

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
《C++ Primer》导学系列：第 18 章 - 用于大型程序的工具
WordPress SEO ☞ WordPress网站终极优化指南
16 条 yyds 的代码规范
PX4编写CAN应用程序控制底盘运动
android中的IME
30 个Python代码实现的常用功能（附案例源码）
VScode远程连接linux
Web开发：属性
前端表单传输数据，后端接收数据的流程
Uni-app + uview 个人信息页 修改用户昵称、性别、个性签名
;