🎉🎉想快速入门数据结构,推荐订阅作者的初阶数据结构专栏!此专栏预计更新:顺序表,链表,栈,队列,二叉树,排序算法等等
🎉🎉初阶数据结构我们通过c语言实现,所以此专栏也可以帮助大家巩固大家的c语言知识
🎉🎉源代码已上传至我的码云
🎉🎉博主的微信公众号关注啦,关注我每天学习一道题,点我关注
前言
我们在前面已经学习了栈这种数据结构,已经了解了它是一种操作受限的线性表,其只能在栈顶进行插入与删除操作,遵循后进先出的规则
而队列,与栈的本质差不多,都是操作受限的线性表,但它却有一些不同的性质
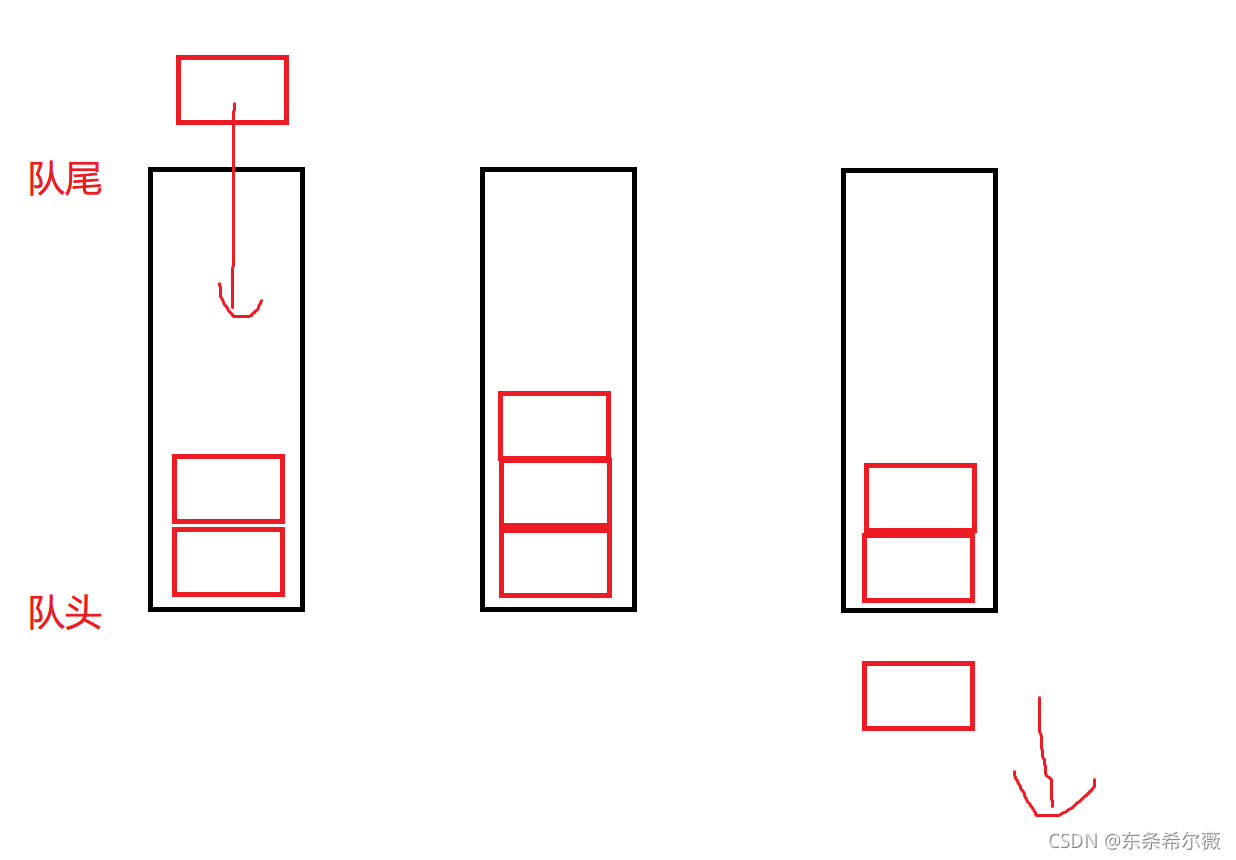
它有两个操作端,队尾和队头,且只能在队头删除数据,只能在队尾插入数据
支持的是先进先出
我们可以形象地理解一下:队列队列,顾明思义就是排队
试想现在是中午,一群人排队去食堂打饭
那肯定是先到的人先打到饭,也就是会先退出这个队伍
队列我们同样可以使用顺序表或者链表实现
但队列这一块没有争议,用链表实现稍好一些
因为我们知道,顺序表要插入和删除的复杂度是O(n)
而链表的插入删除复杂度是O(1)
这个结构不像栈,只在一端进行插入和删除,那样顺序表可以达到O(1)
而它两边都需要操作,那么顺序表总有一端操作的复杂度会达到O(n)
所以队列我们使用链表来实现
队列定义
队列的头文件定义
首先,因为是链表实现,我们要定义一个链表出来,本文使用单链表来实现
typedef struct QueneNode
{
struct QueneNode* next;
QDataType data;
}QNode;
链表的文章我在前面有讲过哦,不懂的小伙伴需要复习功课啦!点我复习
随后就需要定义队列了
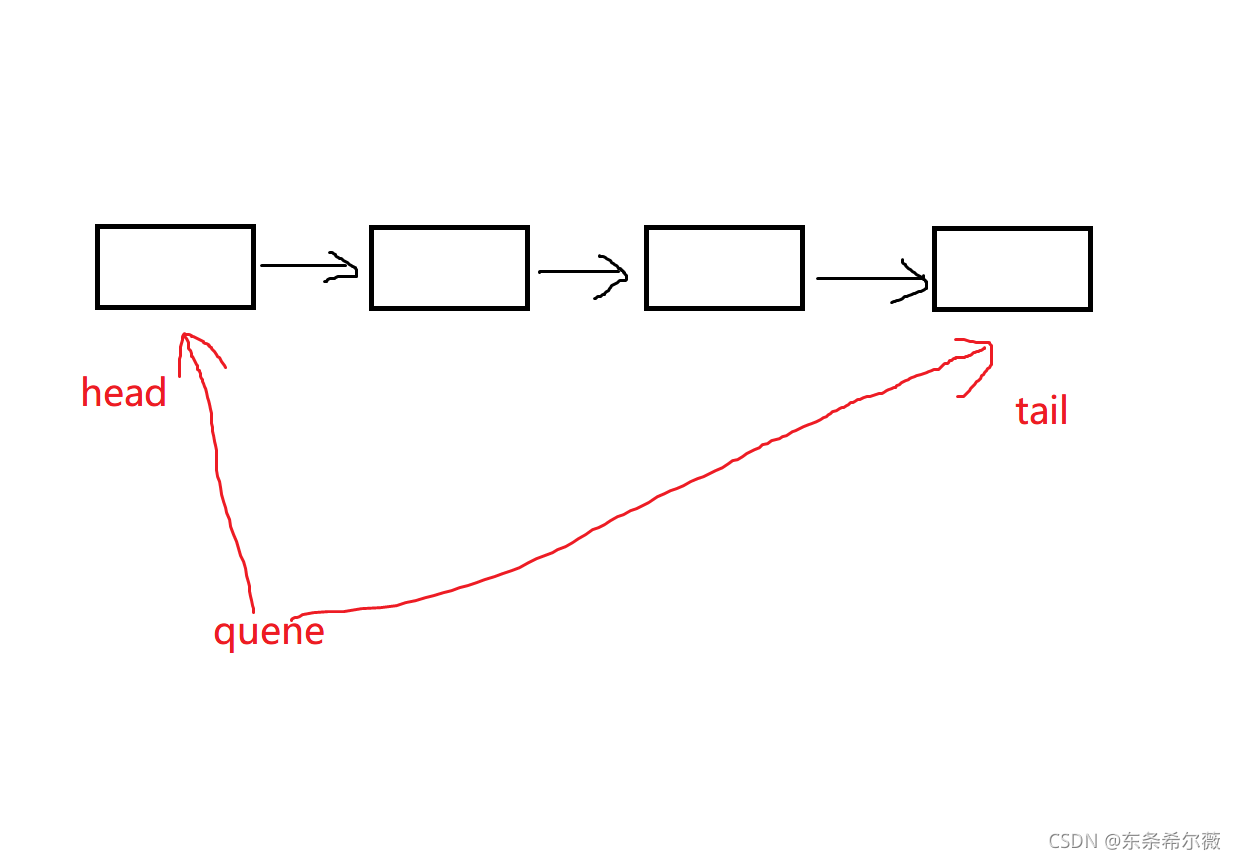
为了方便队列的操作,我们需要两个指针,一个指向头结点head,一个指向尾结点tail
我们知道,单链表的尾部插入的复杂度为O(n),(需要遍历到尾结点),所以定义这两个指针是非常有必要的
typedef struct Quene
{
QNode* front;//指向头结点的指针
QNode* tail;//指向尾结点的指针
}Quene;
随后补全一些代码,完成的我们的定义
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
typedef int QDataType;
typedef struct QueneNode
{
struct QueneNode* next;
QDataType data;
}QNode;
typedef struct Quene
{
QNode* front;
QNode* tail;
}Quene;
队列初始化
因为我们队列中的指针还没有初始化,是野指针,对于野指针我们是零容忍的,所以,我们需要先对它们进行置空
void QueneInit(Quene* pq)
{
assert(pq);
pq->front = NULL;
pq->tail = NULL;
}
队列的插入
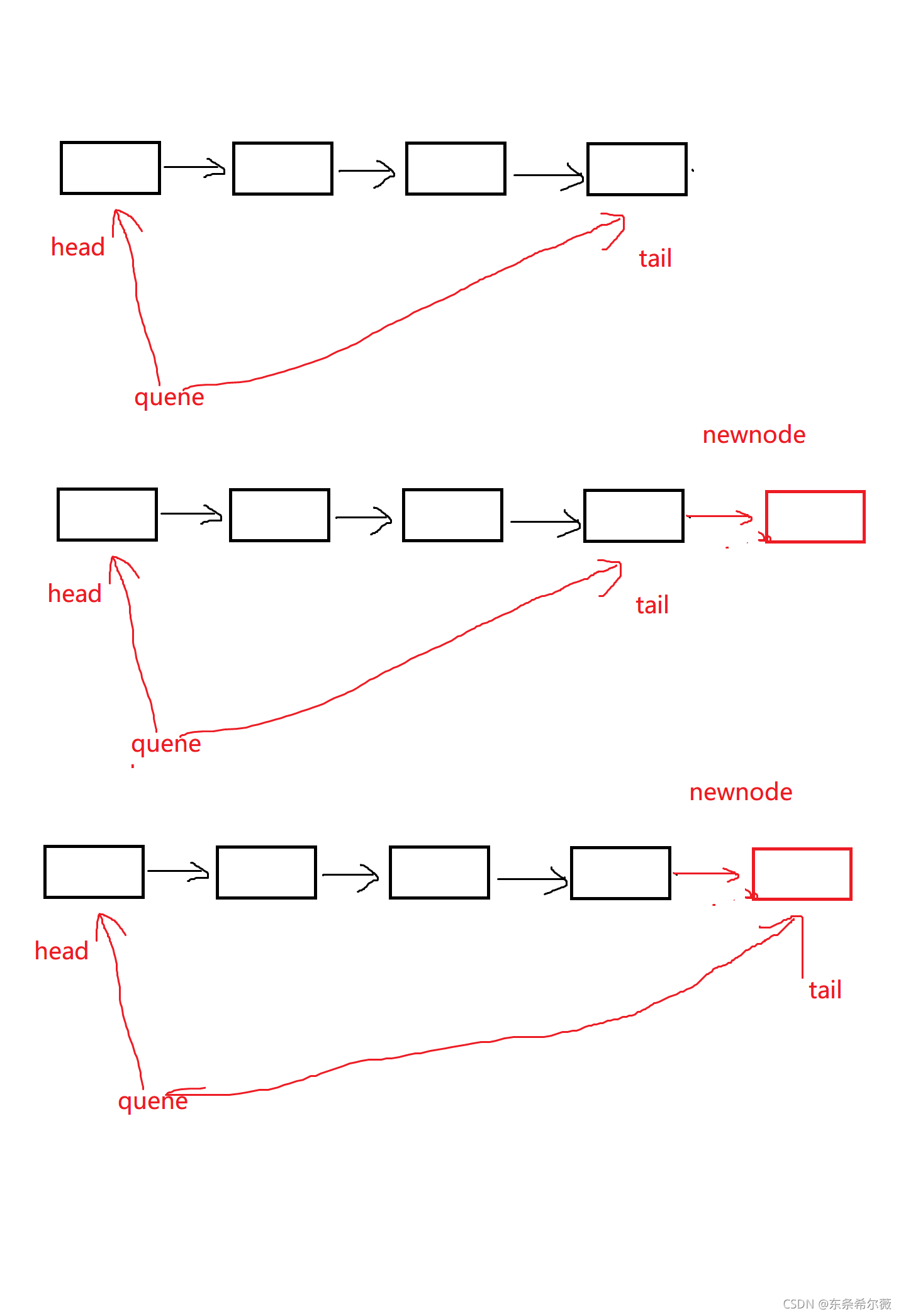
队列我们是在队尾进行插入的,所以我们需要对tail指针进行操作
在tail后面插入一个结点后,再将tail进行更新
可以写出以下代码
void QuenePush(Quene* pq, QDataType x)
{
assert(pq);
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (!newnode)
{
printf("malloc fail\n");
exit(-1);
}
newnode->data = x;
newnode->next = NULL;
//以上是结点开辟的方法,属于单链表的内容
pq->tail->next = newnode;//链接
pq->tail = newnode;//更新
但是有以下的情况:
如果队列为空,我们直接操作的话,就是典型的空指针引用的问题
所以我们需要对这个情况进行特判
然后就完成了完整的代码
void QuenePush(Quene* pq, QDataType x)
{
assert(pq);
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (!newnode)
{
printf("malloc fail\n");
exit(-1);
}
newnode->data = x;
newnode->next = NULL;
if (QueneEmpty(pq))//后文讲到的判空函数
{
pq->front = newnode;
pq->tail = newnode;
}//这个代码块是队列为空的特判
else
{
pq->tail->next = newnode;
pq->tail = newnode;
}
}
队列删除
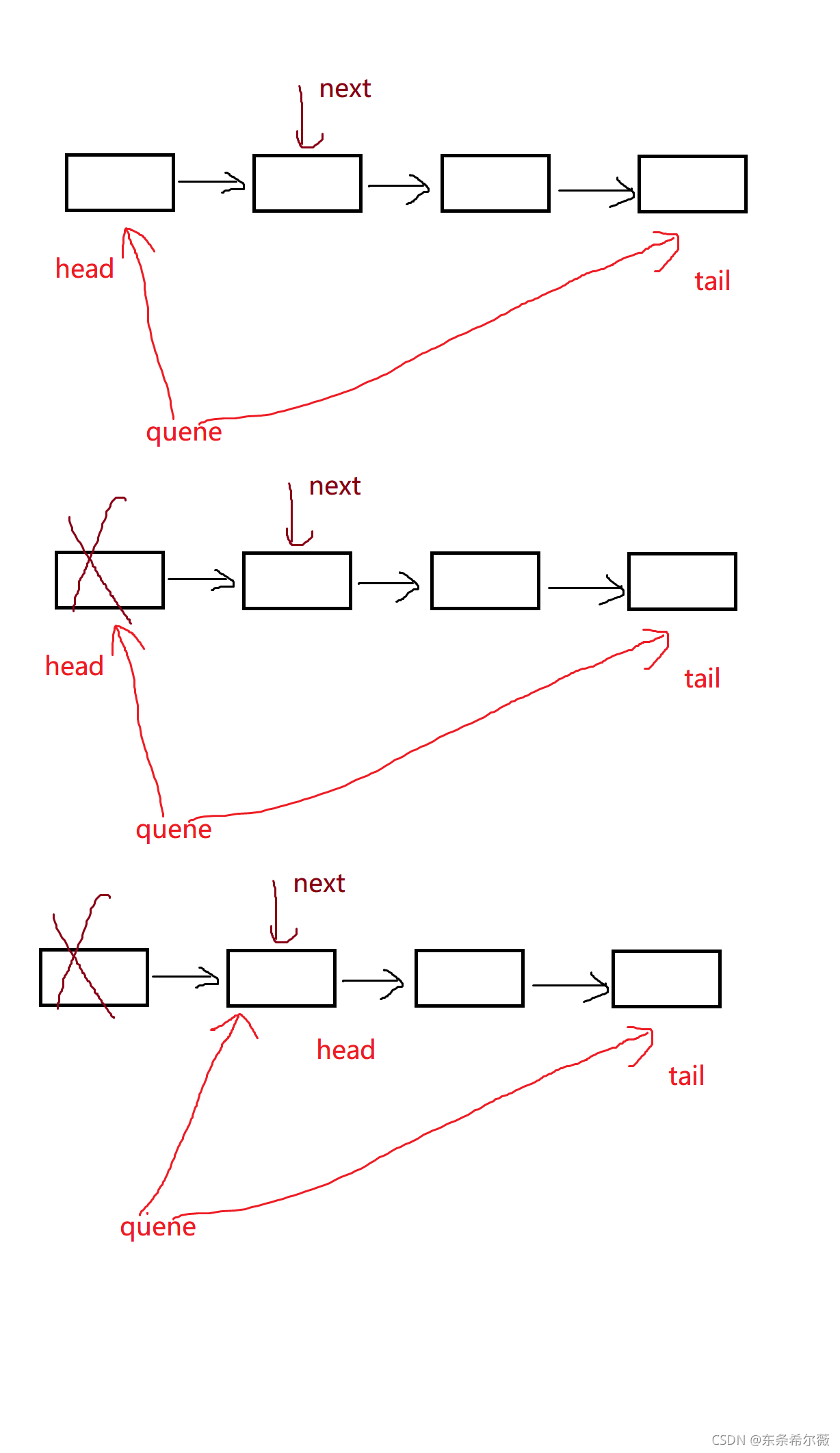
我们只能在队头进行删除,也就是只能对头结点进行操作
因为释放了头结点后,我们就找不到新的头结点了
所以需要一个变量来记录,方便更新头结点
这里有两个问题
首先是队列为空的问题
这个我们已经比较熟悉了,直接assert断言即可
其次是野指针隐患
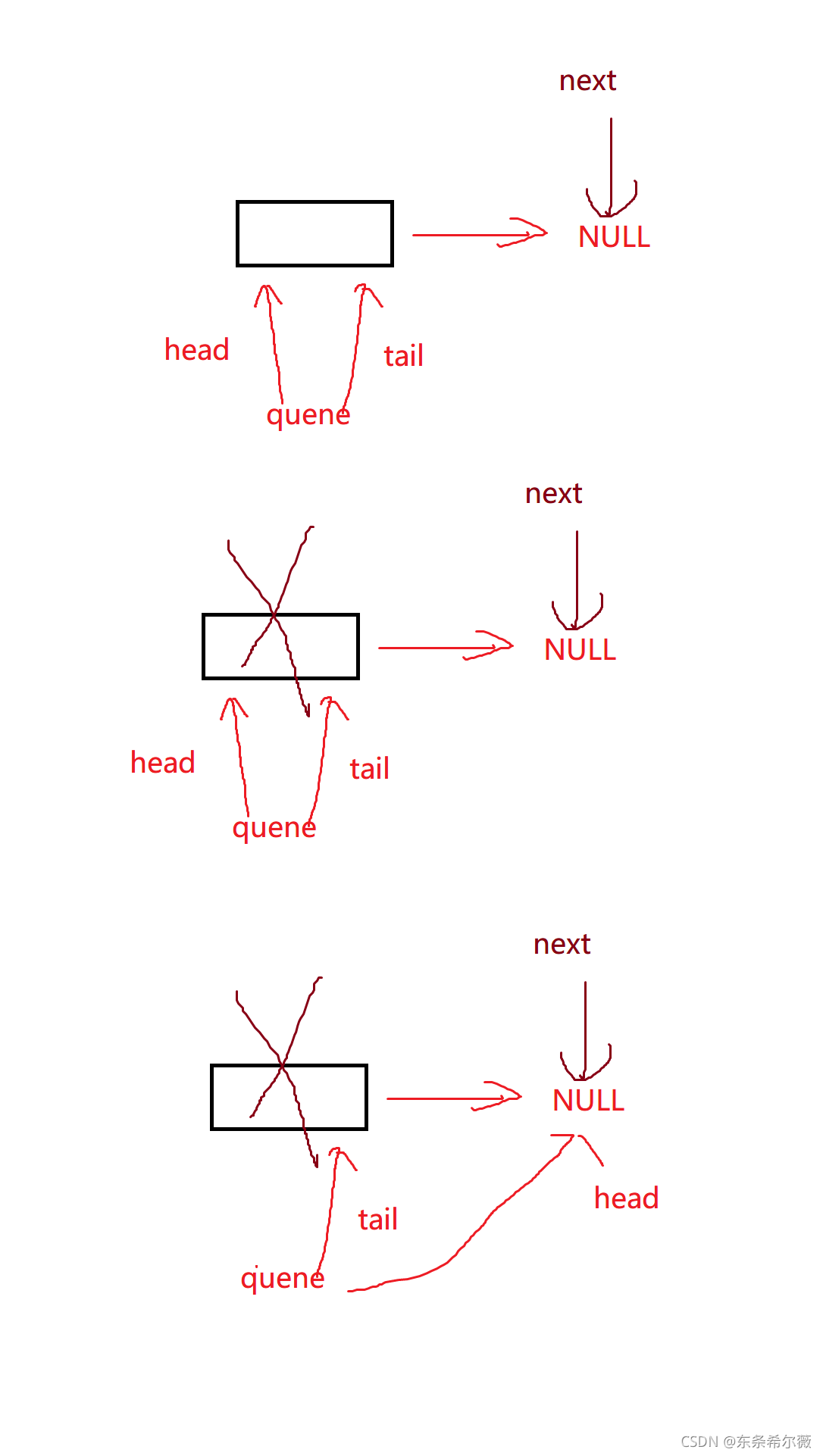
当我们只剩一个结点的时候,如果我们需要删除数据
发现了吗?虽然head被置空了,但是tail却还指向一个已经被释放的结点
为了避免这种情况,需要将tail置空
void QuenePop(Quene* pq)
{
assert(pq);
assert(!QueneEmpty(pq));//空队列特判
QNode* newfront = pq->front->next;
free(pq->front);
pq->front = newfront;
if (!newfront)
{
pq->tail = NULL;//防止野指针
}
}
队列判空
头结点为空即可
bool QueneEmpty(Quene* pq)
{
assert(pq);
return pq->front == NULL;
}
取出队尾和队头的元素
没什么难度,直接返回头指针或者尾指针指向的结点的值即可
QDataType QueneFront(Quene* pq)
{
assert(pq);
assert(!QueneEmpty(pq));
return pq->front->data;
}
QDataType QueneBack(Quene* pq)
{
assert(pq);
assert(!QueneEmpty(pq));
return pq->tail->data;
}
队列大小
这里由于我们没有储存大小,所以需要遍历来算出队列的大小
int QueneSize(Quene* pq)
{
assert(pq);
assert(!QueneEmpty(pq));
int cnt = 0;
QNode* cur = pq->front;
while (cur)
{
cur = cur->next;
cnt++;
}
return cnt;
}
队列销毁
与链表的销毁相同,只是最后要把tail和head给置空
void QueneDestory(Quene* pq)
{
assert(pq);
QNode* cur = pq->front;
while (cur)
{
QNode* next = cur->next;
free(cur);
cur = next;
}
pq->front = pq->tail = NULL;
}