单调栈讲解
问题引入
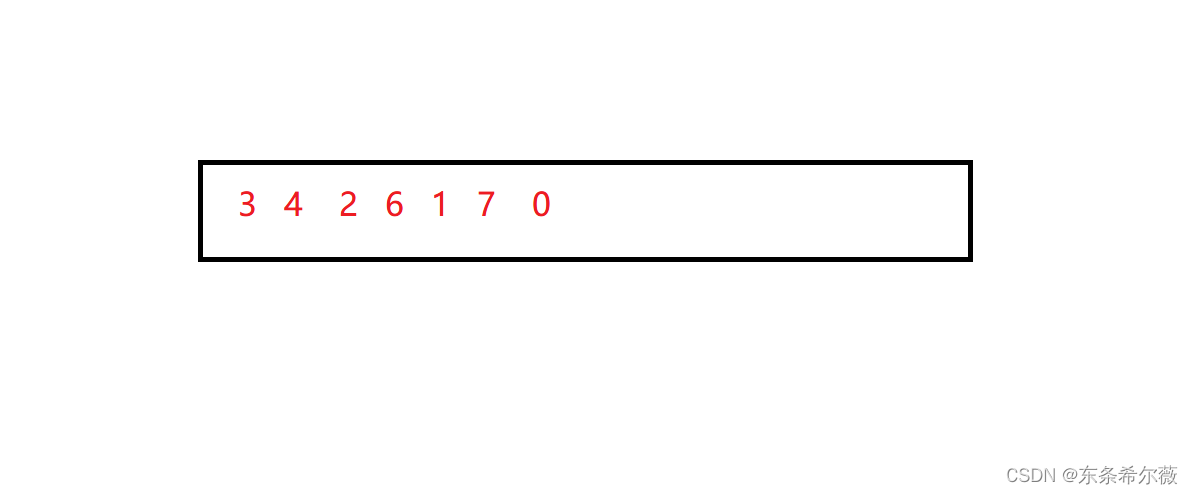
假设我们这儿有一个数组arr
我们现在想得到数组中任意一个数左边第一个比它小(或大)的下标位置和右边第一个比它小(或大)的下标位置的信息
比如上面的数字6,左边第一个比它小的数字是2,对应下标位置是2右边第一个比它小的数字是1,对应下标位置4,所以能生成以下信息
6:[2,4]
而我们规定,左边或者右边没有比其小的数字的话,把答案设为-1
而我们现在需要每个数字的对应信息,这种问题我们该怎么求解呢?
很容易想到暴力方法,我们遍历每一个数字,然后把每个数字往左往右遍历一遍查找符合要求的数字
但是这种方法的时间复杂度比较高(O(n2)),有没有O(n)的办法呢
是有的,就是利用我们的单调栈
单调栈实现
数组中无重复值的单调栈
我们还是拿上面的数组举例
[3,4,2,6,1,7,0]
首先明确一点,我们这里的栈由栈顶底到栈顶必须要严格从小到大的(下文把这个原则简称规则)
我们要遍历这个数组,然后遵循以上的原则入栈
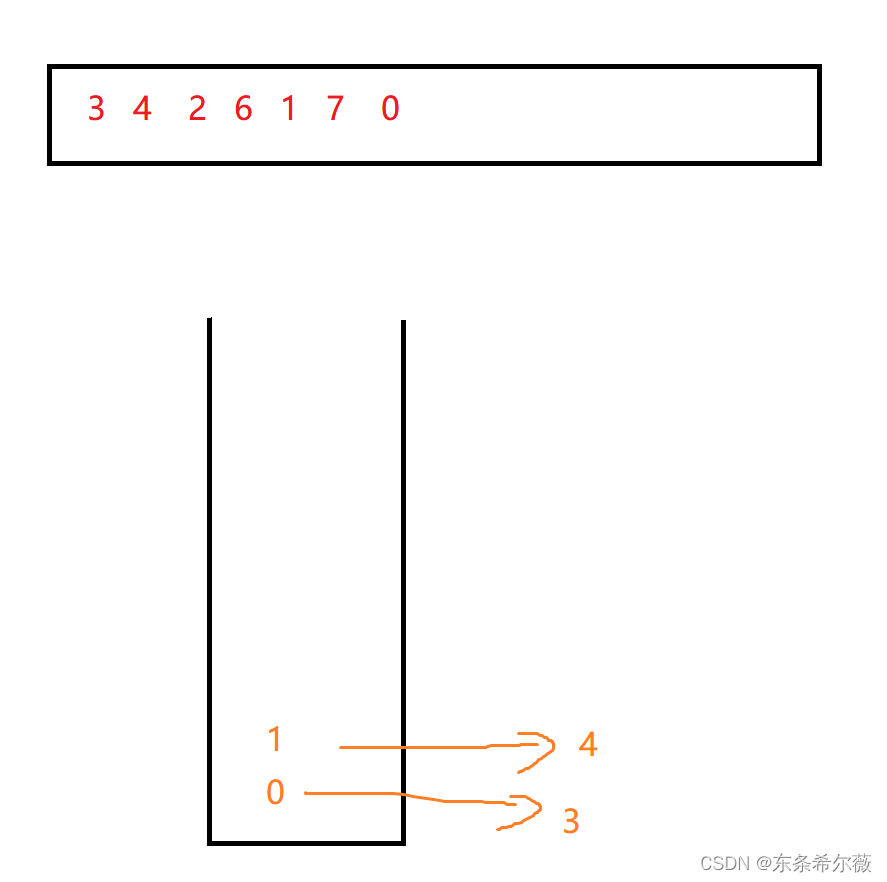
所以我们的3,4能顺序入栈。注意:栈中不是存储数字,而是存储数字对应的下标!
但是当我们下一个数字2要入栈的时候,我们的栈就不遵循我们的原则了,那该怎么办呢?
我们需要弹出栈顶的元素直到重新遵循规则为止。也就是说,要一直弹出元素直到栈顶元素对应数字小于进入的数字或者栈已经空了
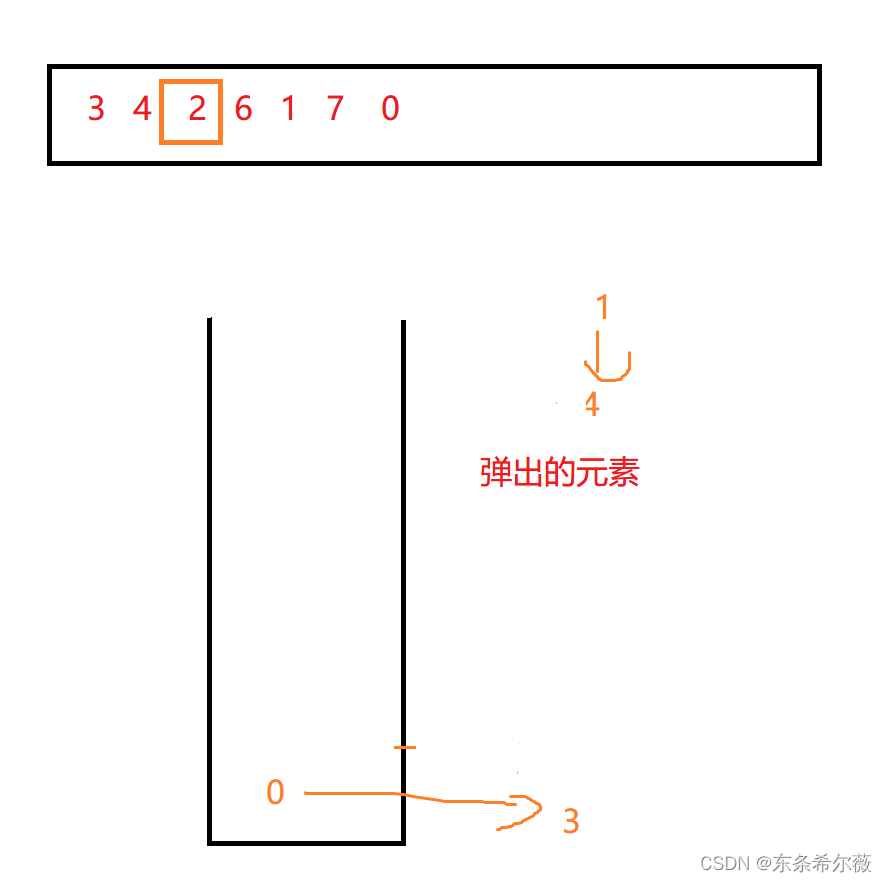
然后就变成了这样
弹出的元素我们以后就见不到了,所以弹出的时候我们要立刻生成信息
生成信息的方式:弹出数字左信息就是当前的栈顶元素,右信息就是准备入栈的元素
所以,我们数字4的信息为:left:0,right:2
但是,本轮还没有完成,因为4弹出后的栈顶元素仍然比2大
所以,我们还需要弹出
本轮弹出中,3栈底没有元素了,所以左信息为-1,而右信息仍然是我们准备入栈的元素
所以,3的信息为:left:-1,right:2
根据这个逻辑,可以写出以下代码
注意:我们的返回值二维数组代表的含义是:第i行代表数组对应的下标位置,它的信息为[left,right]
vector<vector<int>> getNearLessNoRepeat(vector<int>& nums)
{
int n=nums.size();
vector<vector<int>>ans;
for(int i=0;i<n;i++)
{
//初始化我们的答案数组
vector<int>tmp(2,0);
ans.push_back(tmp);
}
stack<int>st;//单调栈
for(int i=0;i<n;i++)
{
while(!st.empty()&&nums[i]<nums[st.top()])
{
//如果栈不为空并且当前数字要进栈已经打破了规则,就弹出数字并且获取信息
int top=st.top();
st.pop();
int leftLess=st.empty()?-1:st.top();//左边信息,有-1的可能性
int rightLess=i;
ans[top][0]=leftLess;
ans[top][1]=rightLess;
}
st.push(i);
}
//遍历完了,但栈中还有元素的情况
//这种情况下,直接一个个弹出,右边信息为-1(没有让它离开的数据),左边信息为当前数字弹出后的栈顶元素
while(!st.empty())
{
int cur=st.top();
st.pop();
int leftLess=st.empty()?-1:st.top();
int rightLess-1;
ans[cur][0]=leftLess;
ans[cur][1]=rightLess;
}
return ans;
}
数组中有重复值的单调栈
有重复值,我们上面的方法就失效了,所以我们需要对我们的结构进行一下改进
我们现在的栈入的元素是一个vector,vector中存储相等数字的下标
例如:【1,1,1】vector中就应该存【0,1,2】
我们在弹出信息的时候也是弹出一个vector,把vector中的每一个下标位置都要计算结果
而我们的信息结果值是取弹出后栈顶的vector的最后一个数字
vector<vector<int>> getNearLess(vector<int>& nums)
{
int n=nums.size();
vector<vector<int>>ans;
for(int i=0;i<n;i++)
{
//初始化我们的答案数组
vector<int>tmp(2,0);
ans.push_back(tmp);
}
stack<vector<int>>st;//单调栈存储vector
for(int i=0;i<n;i++)
{
while(!st.empty()&&nums[i]<nums[st.top()[0]])
{
//如果栈不为空并且当前数字要进栈已经打破了规则,就弹出数字并且获取信息
vector<int> top=st.top();
st.pop();
for(int j=0;j<top.size();j++)
{
//数组中每个元素都要结算
int leftLess=st.empty()?-1:st.top()[st.top().size()-1]
int rightLess=i;
ans[top[j]][0]=leftLess;
ans[top[j]][1]=rightLess;
}
}
//这里判断是否相等还是大于
if(!st.empty()&&nums[i]==nums[st.top()[0]])
{
st.top().push_back(i);
}
else
{
vector<int>tmp={i};
st.push(tmp);
}
}
//遍历完了,但栈中还有元素的情况
//这种情况下,直接一个个弹出,右边信息为-1(没有让它离开的数据),左边信息为当前数字弹出后的栈顶元素
while (!st.empty())
{
vector<int> top = st.top();
st.pop();
for (auto n : top)
{
ans[n][1] = -1;
ans[n][0] = st.empty() ? -1 : st.top()[st.top().size() - 1];
}
}
return ans;
}
单调栈例题
数组中满足条件子数组的最大值
问题描述:
给定一个仅有正数的数组arr。在arr中任意一个子数组sub,我们都可以算出sub中最小值*sub的和。请你返回arr中每个sub的计算结果最大值
思路求解
我们设有以下数组:
[3,2,4,6,5]
我们可以把求子数组的条件优化一下,不用枚举出每个子数组。
显而易见:我们数组中每个位置的数字都可以作为某一个子数组的最小值
我们把每个数字作为最小值的数组列举,总能找出答案来,这样就解决了我们求一个子数组中的最小值
怎么求和的最大值,显而易见:区间在从左边较小值到右边较小值的开区间,这样才能确保当前数组是最小的
单调栈有重复值的话是会失效的,我们怎么改进我们的代码?
我们发现相等的时候,同样弹出元素来计算。但当然,这样算出的是错误的答案
不过没有关系,错了就是错了,因为后面还有一个相等的值在栈里面,总有一次它能算出正确的答案
至于怎么在O(1)时间内算出某个区间的和,也很简单,用前缀和即可
代码实现
int AllTimesMinToMax(vector<int>& nums)
{
int n=nums.size();
int* sum=new int[n];
sum[0]=nums[0];
for(int i=1;i<n;i++)
{
sum[i]+=sum[i-1];
}
stack<int>st;//单调栈
int ans = INT_MIN;
for (int i = 0; i < n; i++)
{
while (!st.empty() && nums[i] <= nums[st.top()])
{
int top = st.top();
st.pop();
int r = i;
ans = max(ans, (st.empty() ? sum[r - 1] : sum[r - 1] - sum[st.top()]));
}
st.push(i);
}
while (!st.empty())
{
int top = st.top();
st.pop();
ans = max(ans, (st.empty() ? sum[n - 1] : sum[n - 1] - sum[st.top()]));
}
return ans;
}
力扣84题
题目描述
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
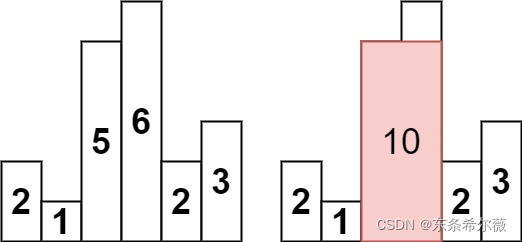
输入:heights = [2,1,5,6,2,3]
输出:10
解释:最大的矩形为图中红色区域,面积为 10
思路求解
木桶原理我们都知道,木桶的盛水量是根据最短的那个木板决定的
这题的计算方法也与木桶原理挂钩,我们同样从每一个数字出发
我们把每一个数字都当做当前能围成区域最短的边,能延伸到的距离设为l,那么,当前的面积为l*nums[i]
就像用例中的5一样,我们把5当做最短的边,那么与它作为最短的边能围成的图形仅为5和6
我们把上面描述的问题可以转化为单调栈问题:同样找到左右较小的值。相等的处理方式与上题同理,图形是连通的,所以最后总是能算对
代码实现
class Solution84 {
public:
int largestRectangleArea(vector<int>& heights) {
int n = heights.size();
stack<int>st;
int ans = INT_MIN;
for (int i = 0; i < n; i++)
{
while (!st.empty() && heights[i] <= heights[st.top()])
{
int top = st.top();
st.pop();
int left = st.empty() ? -1 : st.top();
int right = i - 1;
ans = max(ans, heights[top] * (right - left));
}
st.push(i);
}
while (!st.empty())
{
int top = st.top();
st.pop();
int right = n - 1;
int left = st.empty() ? -1 : st.top();
ans = max(ans, heights[top] * (right - left));
}
return ans;
}
};
力扣85题
问题描述
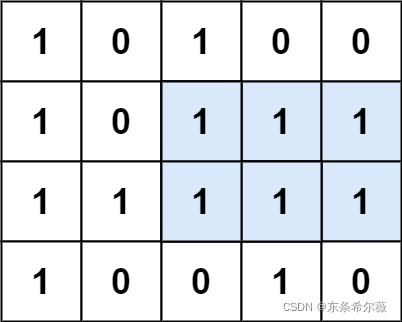
给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
输入:matrix = [[“1”,“0”,“1”,“0”,“0”],[“1”,“0”,“1”,“1”,“1”],[“1”,“1”,“1”,“1”,“1”],[“1”,“0”,“0”,“1”,“0”]]
输出:6
解释:最大矩形如上图所示。
思路求解
这题我们可以使用一个转化的思路:我们可以一行一行的算最大矩形(一个压缩数组的思想)
我们分别把每一行作为地基,然后统计出地基上有多少个1,把它当做面积的话,每一行的求法就和上一题一样了:
一旦遇到0,那么把当然位置设为0,否则+1
例如上面的矩形,它的每一行就为
[1,0,1,0,0]
[2,0,2,1,1]
[3,1,3,2,2]
[4,2,4,3,3]
[5,0,0,4,0]
算出每一行的最大面积就行了(84题方法)
class Solution85 {
public:
int maximalRectangle(vector<vector<char>>& matrix) {
int ans = INT_MIN;
int col = matrix[0].size();
int row = matrix.size();
vector<int>tmp(col, 0);
for (int i = 0; i < row; i++)
{
for (int j = 0; j < col; j++)
{
if (matrix[i][j] == '0')
{
tmp[j] = 0;
}
else
{
tmp[j] += matrix[i][j] - '0';
}
}
ans = max(ans, Solution84().largestRectangleArea(tmp));
}
return ans;
}
};
力扣1504
问题描述
给你一个只包含 0 和 1 的 rows * columns 矩阵 mat ,请你返回有多少个 子矩形 的元素全部都是 1 。
输入:mat = [[1,0,1],
[1,1,0],
[1,1,0]]
输出:13
解释:
有 6 个 1x1 的矩形。
有 2 个 1x2 的矩形。
有 3 个 2x1 的矩形。
有 1 个 2x2 的矩形。
有 1 个 3x1 的矩形。
矩形数目总共 = 6 + 2 + 3 + 1 + 1 = 13 。
思路求解
与上题类似,我们可以算出算出每一行作为地基的情况下,有多少个全1矩形
我们需要算出以某个数字为最小边的区域,它上面的矩形有多少个
因为如果不算上面,以后的数字可能更小,就再也没机会算了
怎么算某个区域的矩形有多少个呢?
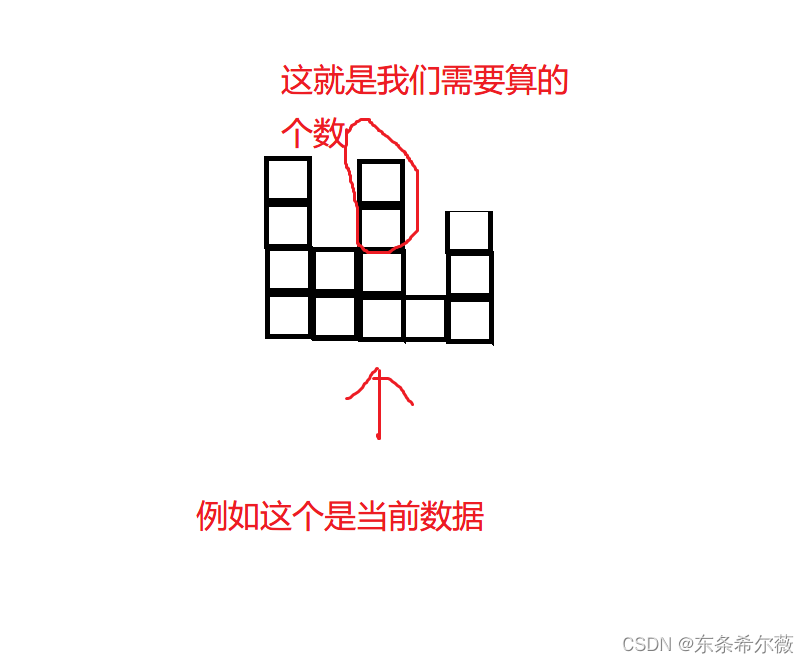
例如有以下图形【4,5】,我们要算以4作为高度的图形
我们可以从上往下算,以高度4作为地基的图形有多少个一直到高度为0作为地基的图形有多少个
从左到右,由数学知识总共有1+2+。。。+l个(l为区域总长度)
每个高度都算一次,所以总共矩形个数为:[(l*(l+1))/2]*h[top]-h[max(left,right)]
最后我们为了防止重复计算,所以遇到相等数据我们不做处理,而且总有最后一个相等值帮助我们计算
代码实现
class Solution1504 {
public:
int numSubmat(vector<vector<int>>& mat) {
int row = mat.size();
int col = mat[0].size();
int ans = 0;
vector<int>tmp(col, 0);
for (int i = 0; i < col; i++)
{
tmp[i] = mat[0][i];
}
for (int i = 0; i < row; i++)
{
for (int j = 0; j < col; j++)
{
if (mat[i][j] == 0)
{
tmp[j] = 0;
}
else
{
tmp[j] += mat[i][j];
}
}
ans += func(tmp);
}
}
int func(vector<int>& tmp)
{
stack<int>st;
int ans = 0;
for (int i = 0; i < tmp.size(); i++)
{
while (!st.empty() && tmp[st.top()] >= tmp[i])
{
int top = st.top();
st.pop();
if (tmp[i] != tmp[top])
{
int left = st.empty() ? -1 : st.top();
int l = i - left - 1;
int down = max(left == -1 ? 0 : tmp[left], tmp[i]);
ans += (tmp[top] - down) * ((l * (l + 1)) >> 1);
}
}
st.push(i);
}
while (!st.empty())
{
int top = st.top();
st.pop();
int left = st.empty() ? -1 : st.top();
int l = tmp.size() - left - 1;
int down = left == -1 ? 0 : tmp[left];
ans += (tmp[top] - down) * ((l * (l + 1)) >> 1);
}
return ans;
}
};
力扣907题
问题描述:
给定一个整数数组 arr,找到 min(b) 的总和,其中 b 的范围为 arr 的每个(连续)子数组。
由于答案可能很大,因此 返回答案模 10^9 + 7 。
思路求解:
首先,根据上面几道题的经验,我们可以通过每一个数字作为最小值来求子数组有多少个
比如:有一个数组满足:
arr[10]=7,左边比arr小的数字在5,右边比arr大的数字在15
那么,我们求的子数组可以有[5-7],[5-8],…[5,14]
[6-7],[6-8],…[6,14]
…
[7-7],[7-8],…[7,14]
子数组必须要包含7
以这个数作为最小值的答案为(7-5)*(14-7)*7
我们只需要记录每个位置左边,右边的信息就行了
如果有相等的值该怎么处理?
我们可以这样防止重复计算
左边找小于等于的数字计算,右边只找小于的数字
class Solution {
public:
vector<int> nearLeft(vector<int>& arr)
{
int n=arr.size();
vector<int>left(n,0);
stack<int>st;
for(int i=n-1;i>=0;i--)
{
while(!st.empty()&&arr[i]<=arr[st.top()])
{
int top=st.top();
st.pop();
left[top]=i;
}
st.push(i);
}
while(!st.empty())
{
int top=st.top();
st.pop();
left[top]=-1;
}
return left;
}
vector<int> nearRight(vector<int>& arr)
{
int n=arr.size();
vector<int>right(n,0);
stack<int>st;
for(int i=0;i<n;i++)
{
while(!st.empty()&&arr[i]<arr[st.top()])
{
int top=st.top();
st.pop();
right[top]=i;
}
st.push(i);
}
while(!st.empty())
{
int top=st.top();
st.pop();
right[top]=n;
}
return right;
}
int sumSubarrayMins(vector<int>& arr) {
long ans=0;
vector<int>left=nearLeft(arr);
vector<int>right=nearRight(arr);
for(int i=0;i<arr.size();i++)
{
long start=i-left[i];
long end=right[i]-i;
ans+=start*end*(long)arr[i];
ans%=1000000007;
}
return (int)ans;
}
};