二分一般适合解决最大的最小值问题，最小的最大值问题；二分的优秀的时间复杂化度使得问题变得更加简单而具体。像这样一个题目：

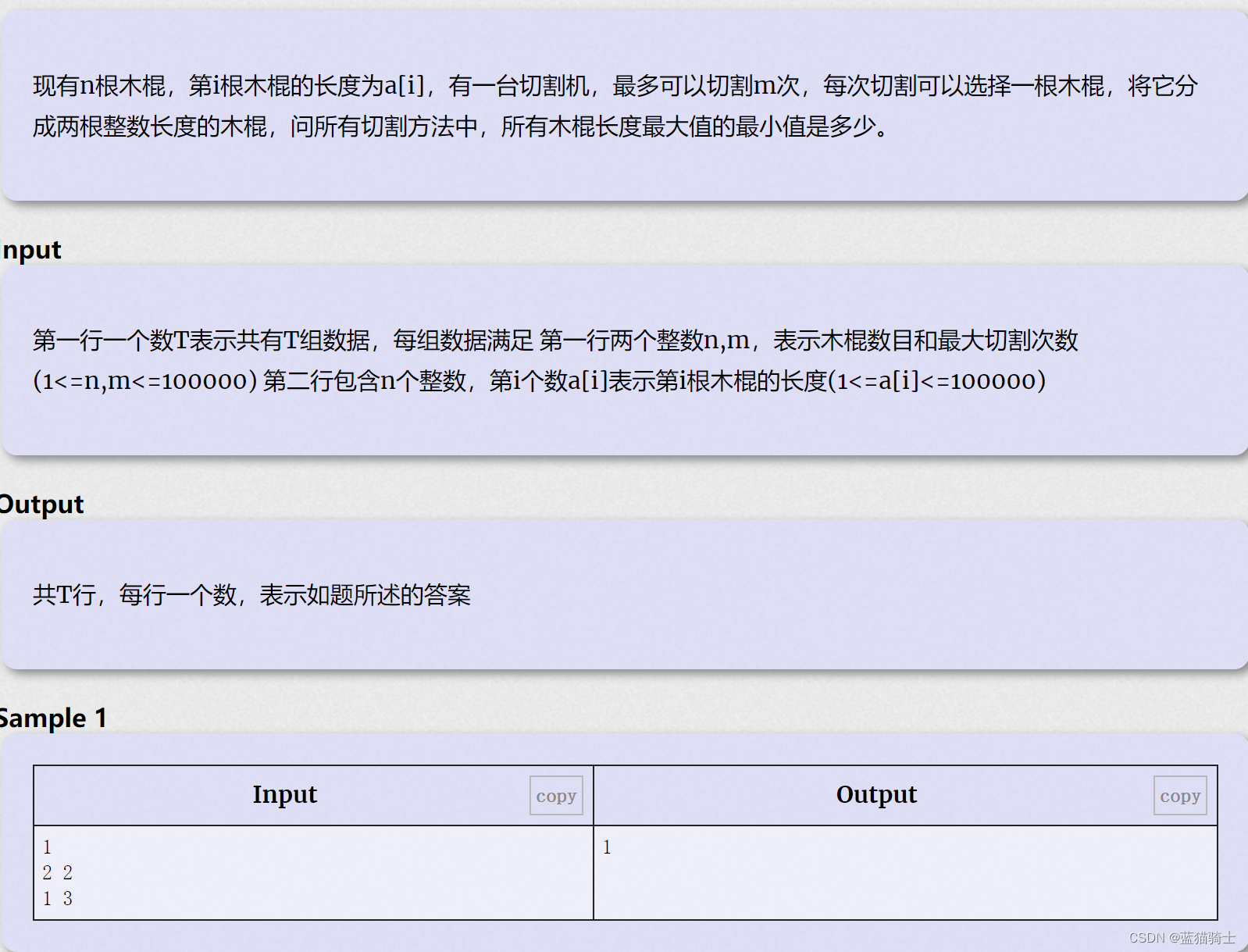
1.木棍问题：

解析：

 由题意可知：我们要求木棍的最大长度的最小值；先假设木棍的最大长度的最小值为 mid；那么所有的比 mid 大的木棍都要进行切割 ( arr[ i ] - 1 ) / mid 的次数；判断一轮 for 循环之后   切割的总次数 与 限制的 M 来进行比较 如果 sum < M; mid 成立；接下来就是二分的问题：确定left与right 的范围： left == 0；right == max（arr[ i ] ）;如果 第一个mid 不成立的话，比所有 比mid 小的值 就一定都不成立；如果mid成立就代表所有比 mid 大的也都成立 ；然后进行迭代 就能找到最佳值进行输入。

#include<bits/stdc++.h>
using namespace std;
int n, m;
int maxn = -1;
int arr[100001] = { 0 };
int num = 0;
int solve() {
	int left = 1;
	int right = maxn;
	int mid;
	while (left <= right ) {
		mid = left + right >> 1;
		for (int i = 1; i <= n; i++) {
			num += (arr[i] - 1) / mid;
		}
		if (num <= m)
			right = mid;
		else
			left = mid + 1;
		num = 0;
		if ((mid == left)&&(left == right))
			break;
	}
	return mid;
}

int main() {
	int T = 0;
	scanf("%d", &T);
	while (T--) {
		scanf("%d%d", &n, &m);
		for (int i = 1; i <= n; i++) {
			scanf("%d", &arr[i]);
			if (arr[i] > maxn)
				maxn = arr[i];
		}
		int ans = solve();
		printf("%d\n", ans);
		maxn = -1;
	}
	return 0;
}

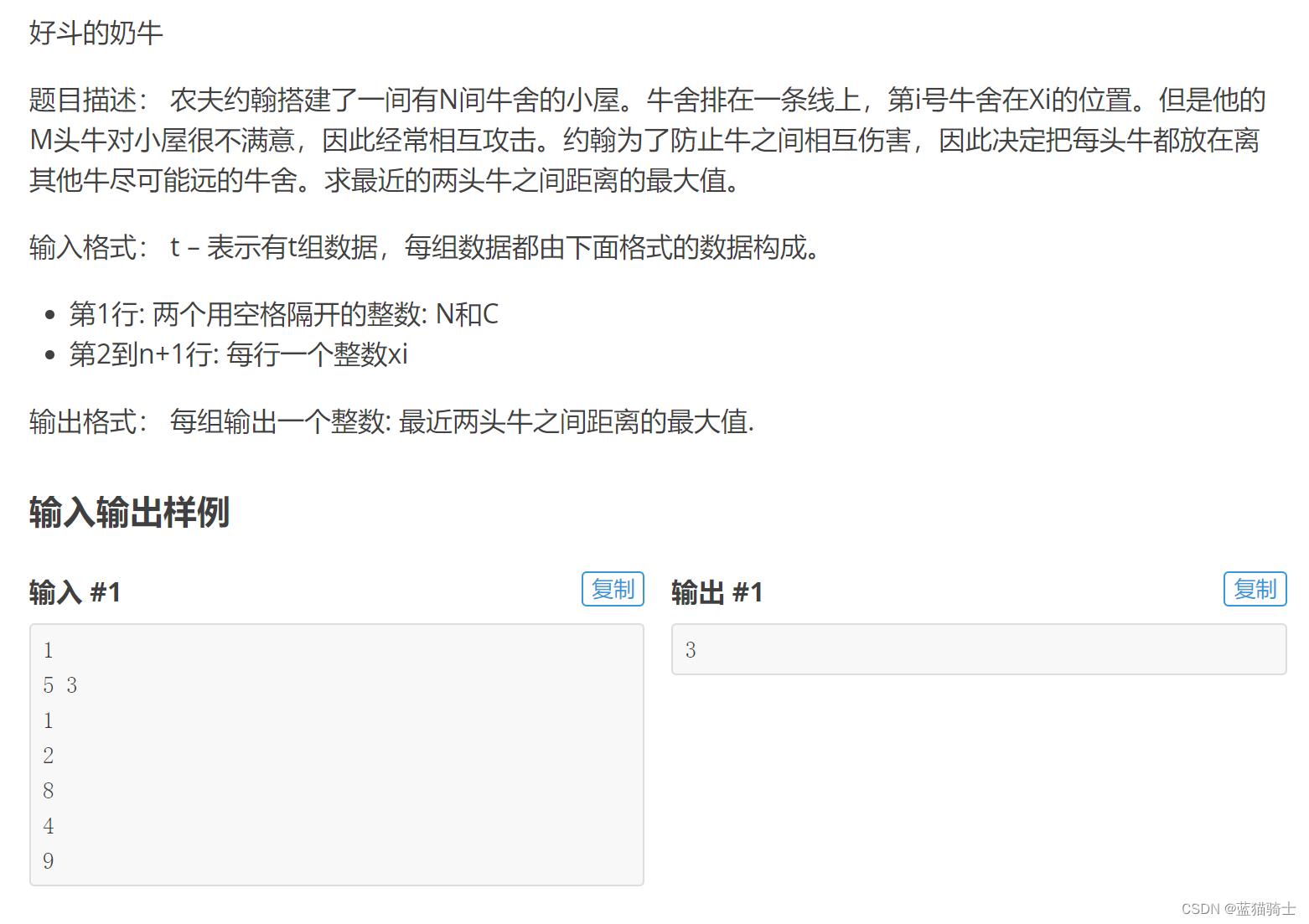
 2.好斗的奶牛：Aggressive cows

 解析：

先对牛舍进行排序；将牛舍的位置按照升序的方式进行排序。 将第一头牛放入第一个牛舍；思考第二头牛应该放在哪里？  先假设 最大的两头牛之间最近的距离为mid, 那么第二头牛的位置应该满足 ： Xi + mid  < = Xj  ;（Xi代表 第一头牛的牛舍位置，Xj代表 第二头牛的牛舍位置）。利用这一一点就可以进行判断取值；

#include<bits/stdc++.h>
using namespace std;
int N, M; int arr[100001] = { 0 };

bool solve(int mid) {
	int cur = 0;
	for (int i = 1; i < M; i++) {  // 加入三头牛，需要三间牛舍 第一次确定两间牛舍，其余都是一间牛舍。
		int last = cur + 1;        // 迭代 判断牛舍  last代表当前最后一间牛舍的位置信息
								   // cur 代表前一个牛舍 的位置信息
		while (last <= N && arr[last] - arr[cur] < mid)// arr[last] - arr[cur] 是两间牛舍的 距离
			last++;                                   // 如果 arr[last] - arr[cur] < mid last 需要向后移动移位；
		if (last > N)
			return 0;
		cur = last;                //迭代 判断牛舍
	} 
	return 1;
}


int main() {
	scanf("%d%d", &N, &M);
	for (int i = 0; i < N; i++)
		scanf("%d", &arr[i]);

	sort(arr, arr + N);  // 将牛舍的位置信息排序
	// 初始化解的存在范围；
	int left = 0, right =  100001;
	while (right - left > 1) {
		int mid = right + left >> 1; // 利用二分 去找合适的mid也就是合适的距离值
		if (solve(mid))
			left = mid;
		else 
			right = mid;
	}
	// 因为是找最大化 最小值问题 （最大化最近的两头牛的距离）
	// 即找          最大值;
	//left 与 right 都一起向 正确的值逼近；
	printf("%d\n", left);
	return 0;
}