目录
第一章 绪论
内容提要:
◆ 数据结构研究的内容。
针对非数值计算的程序设计问题,研究计算机的操作对象以及它们之间的关系和操作。
数据结构涵盖的内容:
◆ 基本概念:数据、数据元素、数据对象、数据结构、数据类型、抽象数据类型。
数据——所有能被计算机识别、存储和处理的符号的集合。
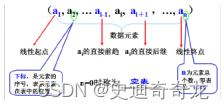
数据元素——是数据的基本单位,具有完整确定的实际意义。
数据对象——具有相同性质的数据元素的集合,是数据的一个子集。
数据结构——是相互之间存在一种或多种特定关系的数据元素的集合,表示为:
Data_Structure=(D, R)
数据类型——是一个值的集合和定义在该值上的一组操作的总称。
抽象数据类型——由用户定义的一个数学模型与定义在该模型上的一组操作,
它由基本的数据类型构成。
◆ 算法的定义及五个特征。
算法——是对特定问题求解步骤的一种描述,它是指令的有限序列,是一系列输入转换为输
出的计算步骤。
算法的基本特性:输入、输出、有穷性、确定性、可行性
◆ 算法设计要求。
①正确性、②可读性、③健壮性、④效率与低存储量需求
◆ 算法分析。
时间复杂度、空间复杂度、稳定性
学习重点:
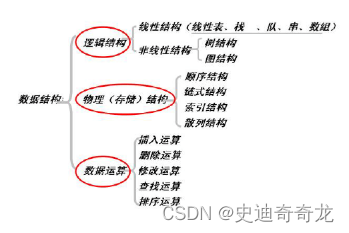
◆ 数据结构的“三要素”:逻辑结构、物理(存储)结构及在这种结构上所定义的操作(运算) 。
◆ 用计算语句频度来估算算法的时间复杂度。
第二章 线性表
内容提要:
◆ 线性表的逻辑结构定义,对线性表定义的操作。
线性表的定义:用数据元素的有限序列表示
◆ 线性表的存储结构:顺序存储结构和链式存储结构。
顺序存储定义:把逻辑上相邻的数据元素存储在物理上相邻的存储单元中的存储结构。
链式存储结构: 其结点在存储器中的位置是随意的,即逻辑上相邻的数据元素在物理上不一
定相邻。通过指针来实现!
1) 修改——通过数组的下标便可访问某个特定元素并修改之。
核心语句: V[i]=x;
顺序表修改操作的时间效率是 O(1)
2) 插入——在线性表的第i个位置前插入一个元素
实现步骤:
①将第n至第i 位的元素向后移动一个位置;
②将要插入的元素写到第i个位置;
③表长加1。
注意:事先应判断: 插入位置i 是否合法?表是否已满?
应当符合条件: 1≤i≤n+1 或 i=[1, n+1]
核心语句:
for (j=n; j>=i; j--)
a[j+1]=a[ j ];
a[ i ]=x;
n++;
插入时的平均移动次数为:n(n+1)/2÷(n+1)=n/2≈O(n)
3) 删除——删除线性表的第i个位置上的元素
实现步骤:
①将第i+1 至第n 位的元素向前移动一个位置;
②表长减1。
注意:事先需要判断,删除位置i 是否合法?
应当符合条件:1≤i≤n 或 i=[1, n]
核心语句:
for ( j=i+1; j<=n; j++ )
a[j-1]=a[j];
n--;
顺序表删除一元素的时间效率为:T(n)=(n-1)/2 ≈O(n)
顺序表插入、删除算法的平均空间复杂度为O(1)
单链表:
(1) 用单链表结构来存放26个英文字母组成的线性表(a,b,c,…,z),请写出C语言程序。
#include<stdio.h>
#include<stdlib.h>
typedef struct node{
char data;
struct node *next;
}node;
node *p,*q,*head; //一般需要3个指针变量
int n ; // 数据元素的个数
int m=sizeof(node); /*结构类型定义好之后,每个node类型的长度就固定了,
m求一次即可*/
void build( ) //字母链表的生成。要一个个慢慢链入
{
int i;
head=(node*)malloc(m); //m=sizeof(node) 前面已求出
p=head;
for( i=1; i<26; i++) //因尾结点要特殊处理,故i≠26
{
p->data=i+‘a’-1; // 第一个结点值为字符a
p->next=(node*)malloc(m); //为后继结点“挖坑”!
p=p->next;} //让指针变量P指向后一个结点
p->data=i+‘a’-1; //最后一个元素要单独处理
p->next=NULL ; //单链表尾结点的指针域要置空!
}
}
void display() //字母链表的输出
{
p=head;
while (p) //当指针不空时循环(仅限于无头结点的情况)
{
printf("%c",p->data);
p=p->next; //让指针不断“顺藤摸瓜”
}
}
(2)单链表的修改(或读取)
思路:要修改第i个数据元素,必须从头指针起一直找到该结点的指针p,
然后才能:p>data=new_value
读取第i个数据元素的核心语句是:
Linklist *find(Linklist *head ,int i)
{
int j=1;
Linklist *p;
P=head->next;
While((p!=NULL)&&(j<i))
{
p=p->next;
j++;
}
return p;
} (3).单链表的插入
链表插入的核心语句:
Step 1:s->next=p->next;
Step 2:p->next=s ;
(4).单链表的删除
删除动作的核心语句(要借助辅助指针变量q):
q = p->next; //首先保存b的指针,靠它才能找到c;
p->next=q->next; //将a、c两结点相连,淘汰b结点;
free(q) ; //彻底释放b结点空间
(5).双向链表的插入操作:
设p已指向第 i 元素,请在第 i 元素前插入元素 x:
① ai-1的后继从 ai ( 指针是p)变为 x(指针是s) :
s->next = p ; p->prior->next = s ;
② ai 的前驱从 ai-1 ( 指针是p->prior)变为 x ( 指针是s);
s->prior = p ->prior ; p->prior = s ;
(6).双向链表的删除操作:
设p指向第 i 个元素,删除第 i 个 元素
后继方向:ai-1的后继由 ai ( 指针p)变为 ai+1(指针 p ->next );
p ->prior->next = p->next ;
前驱方向:ai+1的前驱由 ai ( 指针p)变为ai-1 (指针 p -> prior );
p->next->prior = p ->prior ;
◆ 数组的逻辑结构定义及存储
数组: 由一组名字相同、下标不同的变量构成
N维数组的特点:n个下标,每个元素受到n个关系约束
一个n维数组可以看成是由若干个n-1维数组组成的线性表。
存储:事先约定按某种次序将数组元素排成一列序列,然后将这个线性序列存入存储器中。
在二维数组中,我们既可以规定按行存储,也 可以规定按列存储。
设一般的二维数组是A[c1..d1, c2..d2],
则行优先存储时的地址公式为:
二维数组列优先存储的通式为:
◆ 稀疏矩阵(含特殊矩阵)的存储及运算。
稀疏矩阵:矩阵中非零元素的个数较少(一般小于5%)
学习重点:
◆ 线性表的逻辑结构,指线性表的数据元素间存在着线性关系。在顺序存储结构中,元素
存储的先后位置反映出这种线性关系,而在链式存储结构中,是靠指针来反映这种关系的。
◆ 顺序存储结构用一维数组表示,给定下标,可以存取相应元素,属于随机存取的存储结构。
◆ 链表操作中应注意不要使链意外“断开”。因此,若在某结点前插入一个元素,或删除
某元素,必须知道该元素的前驱结点的指针。
◆ 掌握通过画出结点图来进行链表(单链表、循环链表等)的生成、插入、删除、遍历等操作。
◆ 数组(主要是二维)在以行序/列序为主的存储中的地址计算方法。
◆ 稀疏矩阵的三元组表存储结构。
◆ 稀疏矩阵的十字链表存储方法。
补充重点:
1.每个存储结点都包含两部分:数据域和指针域(链域)
2.在单链表中,除了首元结点外,任一结点的存储位置由 其直接前驱结点的链域的值 指示。
3.在链表中设置头结点有什么好处?
头结点即在链表的首元结点之前附设的一个结点,该结点的数据域可以为空,也可存放
表长度等附加信息,其作用是为了对链表进行操作时,可以对空表、非空表的情况以及对首
元结点进行统一处理,编程更方便。
4.如何表示空表?
(1)无头结点时,当头指针的值为空时表示空表;
(2)有头结点时,当头结点的指针域为空时表示空表。
5.链表的数据元素有两个域,不再是简单数据类型,编程时该如何表示?
因每个结点至少有两个分量,且数据类型通常不一致,所以要采用结构数据类型。
6.sizeof(x)—— 计算变量x的长度(字节数);
malloc(m) — 开辟m字节长度的地址空间,并返回这段空间的首地址;
free(p) —— 释放指针p所指变量的存储空间,即彻底删除一个变量。
7.链表的运算效率分析:
(1)查找
因线性链表只能顺序存取,即在查找时要从头指针找起,查找的时间复杂度为 O(n)。
(2) 插入和删除
因线性链表不需要移动元素,只要修改指针,一般情况下时间复杂度为 O(1)。
但是,如果要在单链表中进行前插或删除操作,因为要从头查找前驱结点,所耗时间复杂
度将是 O(n)。
例:在n个结点的单链表中要删除已知结点*P,需找到它的前驱结点的地址,其时间复杂
度为 O(n)