HDLBits答案（2）_状态机（1）

前言

今天刷完状态机的1/3，以下是书写的代码。

题库

1：Fsm1（异步复位）

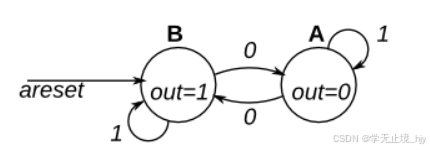
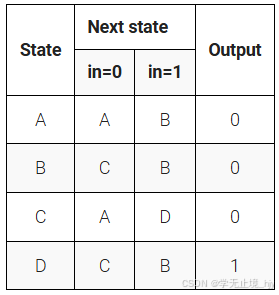
这是一个摩尔状态机，具有两种状态，一种输入，一种输出。实现此状态机。请注意，重置状态为 B。

本练习与FSM1S，但使用异步复位。

Solution： 本题采用两段式描述方法书写

module top_module(
    input clk,
    input areset,    // Asynchronous reset to state B
    input in,
    output out);//  

    parameter A=0, B=1; 
    reg state, next_state;

    always @(posedge clk, posedge areset) begin    // This is a sequential always block
        if(areset)
            state <= B;
        else
            state <= next_state;
    end
    
    always @(*) begin    // This is a combinational always block
        //next_state = B;// State transition logic
        case(state)
            A:if(in == 1'b0) begin
             	  next_state = B;
            	  out <= 1'b0;
            end
              else begin
             	  next_state = A;
            	  out <= 1'b0;
            end
            B:if(in == 1'b0) begin
             	  next_state = A;
            	  out <= 1'b1;
            end
              else begin
             	  next_state = B;
            	  out <= 1'b1;
            end
            default:next_state <= next_state;
        endcase
    end
endmodule

2：Fsm1（同步复位）

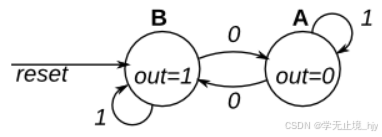
这是一个摩尔状态机，具有两种状态，一种输入，一种输出。实现此状态机。请注意，重置状态为 B。

本练习与FSM1 （英语），但使用同步复位。

Solution： 本题采用两段式描述方法书写

// Note the Verilog-1995 module declaration syntax here:
module top_module(clk, reset, in, out);
    input clk;
    input reset;    // Synchronous reset to state B
    input in;
    output out;//  
    reg out;

    parameter A = 0,B = 1;// Fill in state name declarations

    reg present_state, next_state;
    always @(posedge clk) begin
        if (reset)
            present_state <= B;// Fill in reset logic
        else  
            present_state <= next_state;
    end
    
    always@(*) begin
        next_state = B;
            case (present_state)
                A:if(in == 1'b0) begin// Fill in state transition logic
            		next_state = B;
                    out <= 1'b0;
                end
                  else begin// Fill in state transition logic
            		next_state = A;
                    out <= 1'b0;
                end
                B:if(in == 1'b0)begin// Fill in state transition logic
            		next_state = A;
                    out <= 1'b1;
                end
                  else begin// Fill in state transition logic
            		next_state = B;
                    out <= 1'b1;
                end
                default:next_state = next_state;
            endcase
    end
endmodule

3：Fsm2（异步复位）

这是一个摩尔状态机，具有两种状态，一种输入，一种输出。实现此状态机。请注意，重置状态为 B。

本练习与FSM1 （英语），但使用同步复位。

Solution：

module top_module(
    input clk,
    input areset,    // Asynchronous reset to OFF
    input j,
    input k,
    output out); //  

    parameter OFF=0, ON=1; 
    reg state, next_state;

    always @(posedge clk or posedge areset) begin
        if(areset)// State flip-flops with asynchronous reset
    		state <= OFF;
        else
            state <= next_state;
    end
    
    always @(*) begin
        case(state)// State transition logic
            ON:if(k == 0) begin
                next_state = ON;
                out <= 1'b1;
            end 
            else begin
                next_state = OFF;
                out <= 1'b1;
            end
            OFF:if(j == 0) begin
                next_state = OFF;
                out <= 1'b0;
            end 
            else begin
                next_state = ON;
                out <= 1'b0;
            end
            default:next_state = next_state;
        endcase
    end
endmodule

4：Fsm2（同步复位）

这是一个摩尔状态机，具有两个状态、两个输入和一个输出。实现此状态机。

本练习与FSM2型，但使用同步复位。

Solution：

module top_module(
    input clk,
    input reset,    // Asynchronous reset to OFF
    input j,
    input k,
    output out); //  

    parameter OFF=0, ON=1; 
    reg state, next_state;

    always @(posedge clk) begin
        if(reset)// State flip-flops with asynchronous reset
    		state <= OFF;
        else
            state <= next_state;
    end
    
    always @(*) begin
        case(state)// State transition logic
            ON:if(k == 0) begin
                next_state = ON;
                out <= 1'b1;
            end 
            else begin
                next_state = OFF;
                out <= 1'b1;
            end
            OFF:if(j == 0) begin
                next_state = OFF;
                out <= 1'b0;
            end 
            else begin
                next_state = ON;
                out <= 1'b0;
            end
            default:next_state = next_state;
        endcase
    end
endmodule

5：Fsm3comb

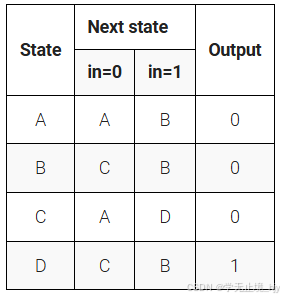
下面是具有一个输入、一个输出和四个状态的摩尔状态机的状态转换表。使用以下状态编码： A=2'b00，B=2'b01，C=2'b10，D=2'b11。
只实现该状态机的状态转换逻辑和输出逻辑（组合逻辑部分）。给定当前状态state（），根据状态转换表计算输出out（）。

Solution：

module top_module(
    input in,
    input [1:0] state,
    output [1:0] next_state,
    output out); //

    parameter A=0, B=1, C=2, D=3;
    always @(*) begin
        case(state)
            A:if(in == 0) begin
            	next_state = A;
                out <= 1'b0	  ;
              end
              else begin
                next_state = B;
				out <= 1'b0	  ;
              end
            B:if(in == 0) begin
            	next_state = C;
                out <= 1'b0	  ;
              end
              else begin
                next_state = B;
				out <= 1'b0	  ;
              end
            C:if(in == 0) begin
            	next_state = A;
                out <= 1'b0	  ;
              end
              else begin
                next_state = D;
				out <= 1'b0	  ;
              end
            D:if(in == 0) begin
            	next_state = C;
                out <= 1'b1	  ;
              end
              else begin
                next_state = B;
				out <= 1'b1	  ;
              end
            default:begin
                next_state = next_state;
                out <= out;
            end
        endcase
    end

endmodule

6：Fsm3onehot

下面是具有一个输入、一个输出和四个状态的摩尔状态机的状态转换表。使用以下单次状态编码： A=4'b0001，B=4'b0010，C=4'b0100，D=4'b1000。
假定使用单次热编码，通过检验推导出状态转换和输出逻辑方程。仅实现该状态机的状态转换逻辑和输出逻辑（组合逻辑部分）。(测试平台将使用非单次热输入进行测试，以确保你没有试图做更复杂的事情）。

        通过检查得出方程是什么意思？
        这意味着只需检查一个状态位，而不是所有状态位，就能确定状态机是否处于特定状态。这样，通过检查状态转换图中每个状态的输入边，就可以得到简单的状态转换逻辑方程。
        例如，在上述状态机中，状态机如何才能到达状态 A？它必须使用两条输入边中的一条： "当前处于状态 A，in=0 "或 "当前处于状态 C，in=0"。由于采用了单击编码，测试 "当前处于状态 A "的逻辑方程就是状态 A 的状态位。单次编码保证了一次最多只有一个子句（乘积项）处于 "活动 "状态，因此这些子句可以直接 OR 在一起。 next_state[0] = state[0]&(~in) | state[2]&(~in)
        当练习要求 "通过检查 "得到状态转换方程时，请使用这种方法。评判员会用非 "一热 "输入进行测试，以确保您的逻辑方程遵循了这种方法，而不会对非法（非 "一热"）的状态位组合采取其他措施（如重置 FSM）。
        虽然知道这种算法对于 RTL 级设计并不是必需的（逻辑合成器会处理这个问题），但它说明了为什么单次热 FSM 通常具有更简单的逻辑（以更多状态位存储为代价），而且这个话题经常出现在数字逻辑课程的考试中。

Solution： 看完题目给的那一大段话，然后照着写就行了。

module top_module(
    input in,
    input [3:0] state,
    output [3:0] next_state,
    output out); //

    parameter A=0, B=1, C=2, D=3;

    // State transition logic: Derive an equation for each state flip-flop.
    assign next_state[A] = (state[A]&(~in))|(state[C]&(~in));
    assign next_state[B] = (state[A]&in)|(state[B]&in)|(state[D]&in);
    assign next_state[C] = (state[B]&(~in))|(state[D]&(~in));
    assign next_state[D] = state[C]&in;

    // Output logic: 
    assign out = state[D];

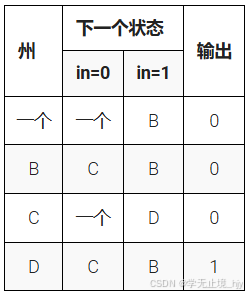
endmodule

7：Fsm3（异步复位）

另请参阅：此 FSM 的状态转换逻辑

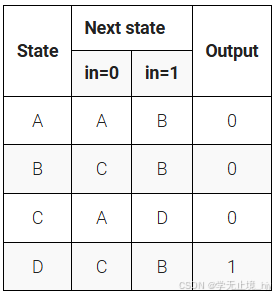
以下是具有一个输入、一个输出和四个状态的摩尔状态机的状态转换表。实现此状态机。包括将 FSM 重置为状态 A 的异步重置。

Solution：

module top_module(
    input clk,
    input in,
    input areset,
    output out); //
	parameter A = 2'b0,B = 2'b1,C = 2'd2,D = 2'd3;
    reg [1:0] state,next_state;
    always @(posedge clk or posedge areset) begin
        if(areset)
            state <= A;
        else
        	state <= next_state;
    end
    
    always @(*) begin
        case(state)
            A:if(in == 0) begin
            	next_state = A;
                out <= 1'b0	  ;
              end
              else begin
                next_state = B;
				out <= 1'b0	  ;
              end
            B:if(in == 0) begin
            	next_state = C;
                out <= 1'b0	  ;
              end
              else begin
                next_state = B;
				out <= 1'b0	  ;
              end
            C:if(in == 0) begin
            	next_state = A;
                out <= 1'b0	  ;
              end
              else begin
                next_state = D;
				out <= 1'b0	  ;
              end
            D:if(in == 0) begin
            	next_state = C;
                out <= 1'b1	  ;
              end
              else begin
                next_state = B;
				out <= 1'b1	  ;
              end
            default:begin
                next_state = next_state;
                out <= out;
            end
        endcase
    end
endmodule

8：Fsm3（同步复位）

另请参阅：此 FSM 的状态转换逻辑

以下是具有一个输入、一个输出和四个状态的摩尔状态机的状态转换表。实现此状态机。包括将 FSM 重置为状态 A 的同步重置（这与 Fsm3 的问题相同，但具有同步重置。

Solution：

module top_module(
    input clk,
    input in,
    input reset,
    output out); //
	parameter A = 2'b0,B = 2'b1,C = 2'd2,D = 2'd3;
    reg [1:0] state,next_state;
    always @(posedge clk) begin
        if(reset)
            state <= A;
        else
        	state <= next_state;
    end
    
    always @(*) begin
        case(state)
            A:if(in == 0) begin
            	next_state = A;
                out <= 1'b0	  ;
              end
              else begin
                next_state = B;
				out <= 1'b0	  ;
              end
            B:if(in == 0) begin
            	next_state = C;
                out <= 1'b0	  ;
              end
              else begin
                next_state = B;
				out <= 1'b0	  ;
              end
            C:if(in == 0) begin
            	next_state = A;
                out <= 1'b0	  ;
              end
              else begin
                next_state = D;
				out <= 1'b0	  ;
              end
            D:if(in == 0) begin
            	next_state = C;
                out <= 1'b1	  ;
              end
              else begin
                next_state = B;
				out <= 1'b1	  ;
              end
            default:begin
                next_state = next_state;
                out <= out;
            end
        endcase
    end
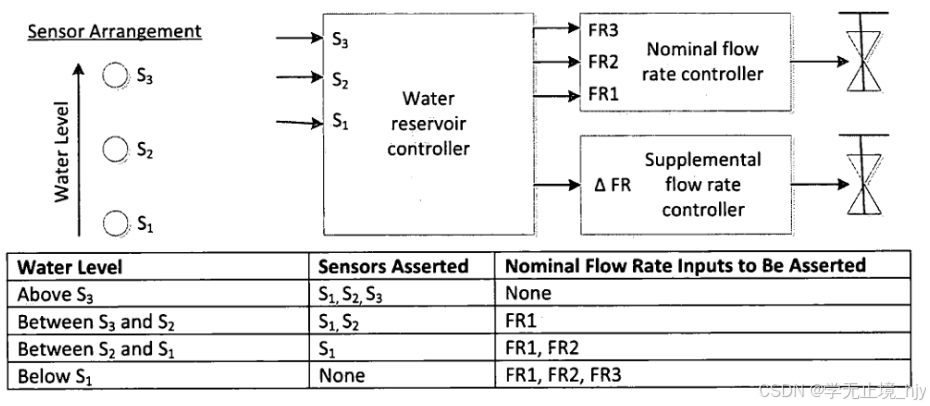
endmodule

9：Design a Moore Fsm

还包括高电平有效同步复位，可将状态机复位到与长时间水位低等效的状态（未断言传感器，并断言所有四个输出）。

Solution：

module top_module (
    input clk,
    input reset,
    input [3:1] s,
    output fr3,
    output fr2,
    output fr1,
    output dfr
); 
    parameter s123 = 4'b0001;
    parameter s23 = 4'b0010;
    parameter s3 = 4'b0100;
    parameter s0 = 4'b1000;
    //设置状态s123：3个传感器未检测到水，s23：s1传感器检测到水，
    //s3：s1和s2检测到水，s0：3个传感器都检测到水
    reg [3:0] state,next_state;
    reg [2:0] fr;
    assign {fr3,fr2,fr1} = fr;
    //第一个进程，同步时序always模块，格式化描述次态寄存器迁移到现态寄存器
    always @(posedge clk) begin//本题采用三段式的写法
        if(reset)
            state <= s123;
        else
            state <= next_state;
    end
    //第二个进程，组合逻辑always模块，描述状态转移条件判断
    always @(*) begin
        case(s) //s3,s2,s1:按顺序排，0代表未检测到水，1代表检测到水。
            3'b000:next_state = s123; //这里采用阻塞赋值
            3'b001:next_state = s23;
            3'b011:next_state = s3;
            3'b111:next_state = s0;
            default:next_state = s123;
        endcase
    end
    //第三个进程，同步时序always模块，格式化描述次态寄存器输出
    always @(posedge clk) begin
        if(reset)
            fr <= 3'b111;
        else begin
        case(next_state) //fr:fr3,fr2,fr1:1代表开进水阀，0代表关进水阀。
            s123:fr <= 3'b111; //这里采用非阻塞赋值
            s23 :fr <= 3'b011;
            s3  :fr <= 3'b001;
            s0  :fr <= 3'b000;
            default:fr <= 3'b111;
        endcase
        end
    end
    //dfr:1代表加快水流入水箱的流速（水位降低，例如从s3到s23，即next_state < state）
    //0代减慢水流入水箱的流速（水位升高，例如从s23到s3,即next_state > state）
    always @(posedge clk) begin
        if(reset)
            dfr <= 1'b1;
        else if(next_state < state)
            dfr <= 1'b1;
        else if(next_state > state)
        	dfr <= 1'b0;
        else
            dfr <= dfr;
    end
    
    
endmodule

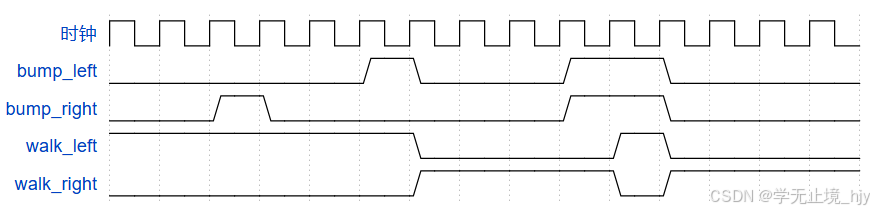
10：Lemmings1

游戏涉及大脑相当简单的小动物。如此简单，我们将使用有限状态机对其进行建模。

在旅鼠的 2D 世界中，旅鼠可以处于两种状态之一：向左走或向右走。如果它撞到障碍物，它会改变方向。特别是，如果旅鼠在左边被撞到，它会向右走。如果它在右边被撞到，它会向左走。如果它同时在两侧颠簸，它仍然会切换方向。

实现具有两个状态、两个输入和一个输出的摩尔状态机，以模拟这种行为。

Solution：

module top_module(
    input clk,
    input areset,    // Freshly brainwashed Lemmings walk left.
    input bump_left,
    input bump_right,
    output walk_left,
    output walk_right); //  

    parameter LEFT=0, RIGHT=1;
    reg state, next_state;
    wire [1:0] bump;
    assign bump = {bump_left,bump_right};

    always @(posedge clk, posedge areset) begin
        if(areset)
            state <= LEFT;
        else
            state <= next_state;
    end

    always @(*) begin
        case(state)
            LEFT:if((bump == 2'b10)||(bump == 2'b11))begin
				    next_state = RIGHT ;
				 end
				 else begin
                    next_state = LEFT ;
                 end
            RIGHT:if((bump == 2'b01)||(bump == 2'b11))begin
				     next_state = LEFT ;
				  end
				  else begin
				     next_state = RIGHT ;
				  end
            
        endcase
    end 

    // Output logic
    assign walk_left = (state == LEFT);
    assign walk_right = (state == RIGHT);

endmodule

参考内容

HDLBits刷题网站：HDLBits (01xz.net)