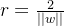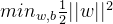支持向量机以及python实现

优点方面：
1. 解决非线性问题：SVM通过使用核技巧，能够有效地处理非线性问题。核技巧可以将数据映射到更高维度的空间中，使得原本线性不可分的数据变得可分。
2. 最大化决策边界：SVM的核心在于寻找一个能够最大化两个类别之间间隔的超平面，这个超平面即为最大间隔超平面。
3. 支持向量的作用：SVM的训练结果中的支持向量在分类决策中起决定作用，这有助于模型的简化和计算效率的提升。
4. 小样本学习：SVM适合小样本学习，它的性能不依赖于样本的维数，而是依赖于支持向量的数量，这避免了维数灾难问题。
缺点方面：
1. 对大规模数据集训练时间长：SVM在训练过程中需要进行大量的矩阵运算，特别是核矩阵的计算，这在大规模数据集上会导致训练时间过长。
2. 对噪声数据敏感：SVM试图拟合所有数据点，包括噪声点，这可能导致模型过拟合，泛化能力下降。
3. 参数调整和核函数选择：SVM的性能很大程度上依赖于核函数的选择和相关参数的调整，这需要用户有一定的专业知识和经验。
4. 主要适用于二分类问题：虽然SVM可以通过一些方法扩展到多类分类问题，但其在二分类问题上的表现更为自然和有效。

为了克服这些缺点，可以采取以下措施：

对于大规模数据集，可以使用近似算法或在线学习算法来减少训练时间。
通过引入软间隔和正则化项，可以增强SVM对噪声数据的鲁棒性。
使用交叉验证等技术来选择最优的核函数和参数。
对于多类分类问题，可以采用一对一或一对多等策略来构建多个二分类器。

1.3 数学理论分析

1.3.1 间隔方程

在样本空间中，划分超平面可通过如下线性方程来描述：

$w^{T}+b=0$

其中 $w^{_{}}$ =( $w_{1}^{}$ ； $w_{2}^{}$ ；...； $w_{d}^{}$ ）是法向量，决定了超平面的方向，b位移项，样本空间中任意点到超平面的距离为

$r=\frac{|w^{T}+b|}{||w||}$

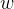
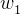
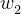
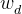
如下图所示，红线代表间隔方程，若超平面（w，b）可以将样本正确分类，则

当yi=1， $w^{T}x_{i}+b>=1$ ；

当yi=-1， $w^{T}x_{i}+b<=-1$

其中两个式子化作等式即为支持向量，上述式子等价于yi $w^{T}x_{i}+b>=1$ ，两个支持向量的间隔就是

$r=\frac{2}{||w||}$

想要找到最大间隔的划分超平面，就满足

$max_{w,b}\frac{2}{||w||},s.t(y{_i}(w^{T}x_{i}+b)>=1)$

由于梯度下降法更适合解决求最小值问题.因此把最优化目标转化最小化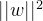 $||w||^{2}$ ,

$min_{w,b}\frac{1}{2}||w||^{2}$ $,s.t \, (y_{i}^{}(w^{T}x_{i}+b)>=1)$

1.3.2 软间隔

软间隔，就是允许一定量的样本分类错误。那为了使样本分类不那么严格，我们引入了松弛因子

$min_{w,b}\frac{1}{2}||w||^{2}$ $+C\sum_{i=1}\varepsilon _{i}^{}$

C为常数项，C的右边部分为松弛因子。当常数项越大，松弛因子越小，说明软间隔越小，相反，则软间隔越大。

当C比较小时，对粗偶五分析的惩罚较小，比较松弛，之间的间隔就比较大，可能产生欠拟合

当C比较大时，对粗偶五分析的惩罚较大，之间的间隔就比较小，可能产生过拟合的情况

C值越大，越不容易放弃那些离群点，C值越小，越不重视离群点

1.3.3 核函数

可以将样本从原始空间映射到一个更高维的特质空间中，使得样本在新的空间中线性可分。这样我们就可以使用原来的推导来进行计算，只是所有的推导是在新的空间，而不是在原来的空间中进行。

$f(x)=w^{T}x_{}+b=\sum_{i=1}^{m}\alpha _{i}y_{i}x_{i}^{T}x+b$ 来说变成 $f(x)=w^{T}x_{}+b=\sum_{i=1}^{m}\alpha _{i}y_{i}\phi (x_{i})^{T}\phi (x)+b$

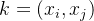
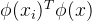
其中 $k=(x_{i},x_{j})$ = $\phi (x_{i})^{T}\phi (x)$ 就是核函数，核函数的选择是支持向量机性能的关键。

常用核函数表：

1.4 应用

支持向量的质量决定了SVM在实际应用中的效果，如文本分类、生物信息学等领域的成功应用很大程度上依赖于支持向量的有效确定。
在处理实际问题时，选择合适的核函数和参数调整对于挖掘出有效的支持向量至关重要。

二、代码实现

2.1分析代码

导入必要的库：
- numpy：用于数值计算。
- pandas：用于数据处理。
- matplotlib.pyplot：用于绘图。
- seaborn：用于高级可视化。
- scipy.io：用于加载MAT文件。
- sklearn：用于机器学习，特别是SVM算法。
准备数据集：
- 使用loadmat函数从MAT文件中加载数据。
- 打印出MAT文件中的键，确认数据集的结构。
- 从MAT文件中提取特征矩阵X和标签向量y。
定义plotData函数：
- 使用matplotlib.pyplot绘制散点图，其中X是特征，y是标签。
- 设置图表大小、颜色映射、坐标轴标签等。
定义plotBoundary函数：
- 计算决策边界的范围，并创建一个网格。
- 使用SVM模型预测网格上的点，得到决策边界。
- 使用contour函数绘制决策边界。
创建SVM模型：
- 创建两个SVM模型，分别对应不同的C值（1和100）。
- C是SVM的正则化参数，控制模型对误分类的惩罚程度。
训练SVM模型：
- 使用fit方法训练两个SVM模型。
评估SVM模型：
- 使用score方法评估两个SVM模型的准确率。
定义plot函数：
- 为每个SVM模型创建一个图表。
- 绘制数据点和决策边界。
- 设置图表标题。
绘制图表：
- 调用plot函数绘制图表。
- 使用plt.show()显示所有图表。
运行代码：
- 执行代码，加载数据，训练模型，绘制图表，并显示结果。

这段代码展示了如何使用SVM进行分类，并绘制出决策边界。通过调整C值，可以看到模型对误分类的敏感度如何影响决策边界的形状。

2.2 完整代码

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sb
from scipy.io import loadmat
from sklearn import svm

'''
1.Prepare datasets
'''
mat = loadmat('D:\\ex6data1.mat')
print(mat.keys())
# dict_keys(['__header__', '__version__', '__globals__', 'X', 'y'])
X = mat['X']
y = mat['y']
'''大多数SVM的库会自动帮你添加额外的特征x0,所以无需手动添加。'''

def plotData(X, y):
    plt.figure(figsize=(8, 6))
    plt.scatter(X[:, 0], X[:, 1], c=y.flatten(), cmap='rainbow')
    # c=list，设置cmap，根据label不一样，设置不一样的颜色
    # c:色彩或颜色序列   camp:colorap（颜色表）
    plt.xlabel('x1')
    plt.ylabel('x2')
    # plt.legend()
    # plt.grid(True)
    # # plt.show()
    pass

# plotData(X, y)
def plotBoundary(clf, X):
    '''Plot Decision Boundary'''
    x_min, x_max = X[:, 0].min() * 1.2, X[:, 0].max() * 1.1
    y_min, y_max = X[:, 1].min() * 1.1, X[:, 1].max() * 1.1
    # np.linspace(x_min, x_max, 500).shape---->(500, )  500是样本数
    # xx.shape, yy.shape ---->(500, 500) (500, 500)
    xx, yy = np.meshgrid(np.linspace(x_min, x_max, 500), np.linspace(y_min, y_max, 500))
    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
    # model.predict:模型预测 (250000, )
    # ravel()将多维数组转换为一维数组 xx.ravel().shape ----> (250000,1)
    # np.c 中的c是column（列）的缩写，就是按列叠加两个矩阵，就是把两个矩阵左右组合，要求行数相等。
    # np.c_[xx.ravel(), yy.ravel()].shape ----> (250000,2) 就是说建立了250000个样本
    Z = Z.reshape(xx.shape)
    plt.contour(xx, yy, Z)
    # 等高线得作用就是画出分隔得线
    pass

models = [svm.SVC(C=C, kernel='linear') for C in [1, 100]]
# 支持向量机模型 (kernel:核函数选项，这里是线性核函数 , C:权重，这里取1和100)
# 线性核函数画的决策边界就是直线
clfs = [model.fit(X, y.ravel()) for model in models]    # model.fit:拟合出模型
score = [model.score(X, y) for model in models]        # [0.9803921568627451, 1.0]
# title = ['SVM Decision Boundary with C = {}(Example Dataset 1)'.format(C) for C in [1, 100]]

def plot():
    title = ['SVM Decision Boundary with C = {}(Example Dataset 1)'.format(C) for C in [1, 100]]
    for model, title in zip(clfs, title):
        # zip() 函数用于将可迭代的对象作为参数，将对象中对应的元素打包成一个个元组，然后返回由这些元组组成的列表。
        plt.figure(figsize=(8, 5))
        plotData(X, y)
        plotBoundary(model, X)  # 用拟合好的模型（预测那些250000个样本），绘制决策边界
        plt.title(title)
        pass
    pass

plot()
plt.show()

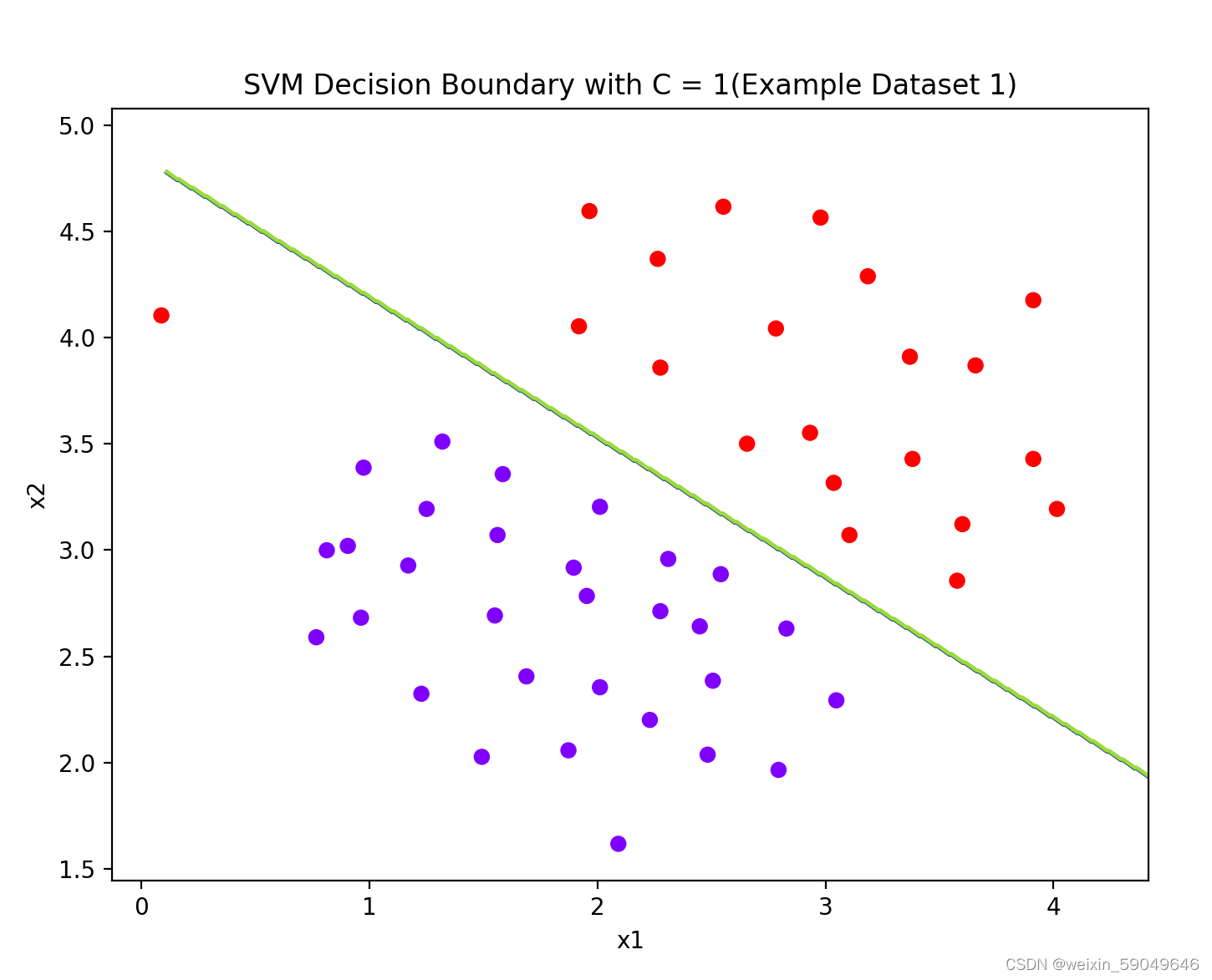
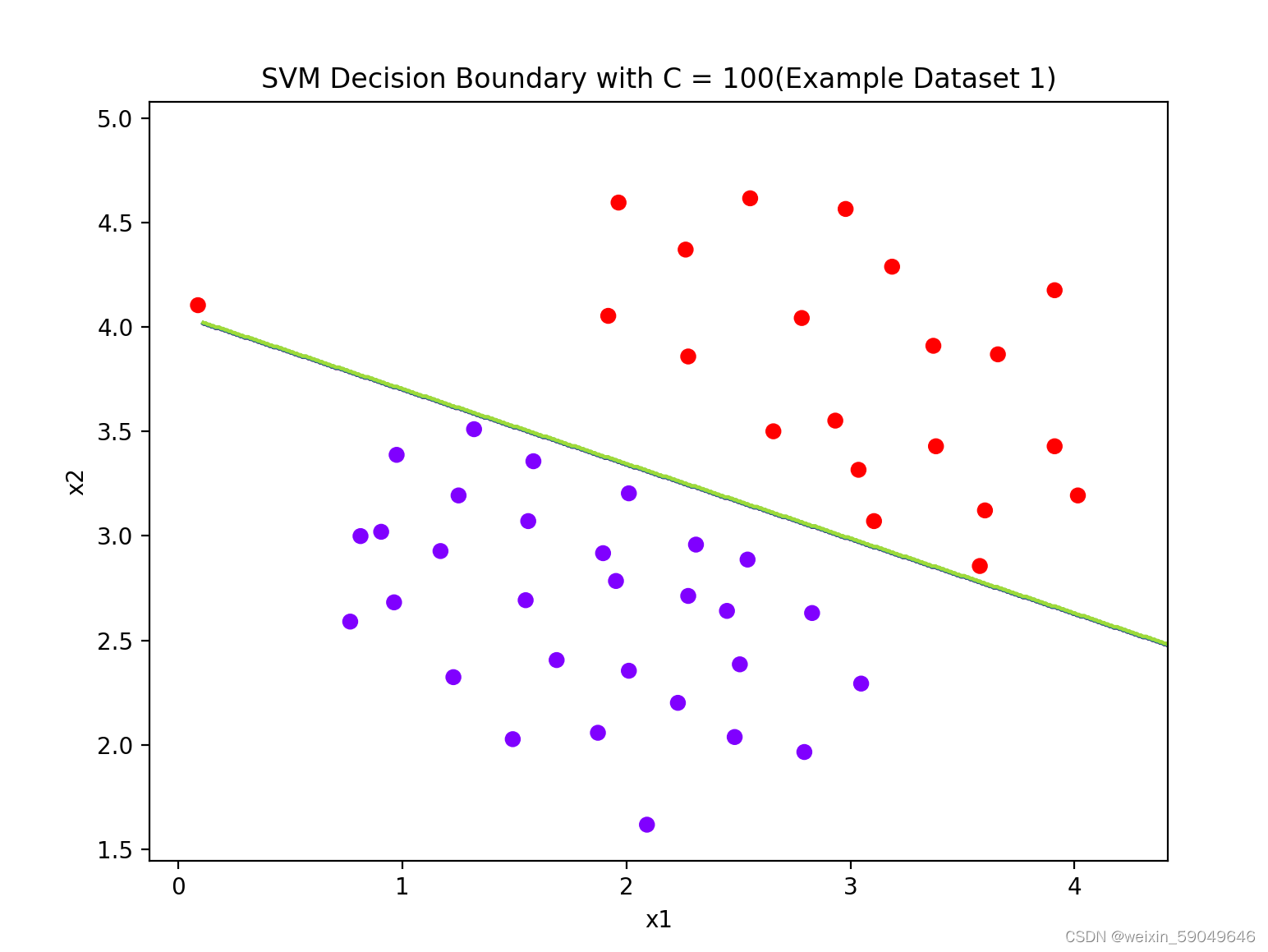
2.3 运行结果：

2.4 实验结论

通过这个实验，我们可以得到以下关于C的结论：

1. 当C值较大时（如100），模型对训练数据的拟合较好，准确率较高。这意味着在这种情况下，模型对训练数据中的噪声和异常值更加敏感，可能会导致过拟合。

2. 当C值较小时（如1），模型对训练数据的拟合较差，准确率较低。这意味着在这种情况下，模型对训练数据中的噪声和异常值不太敏感，可能会导致欠拟合。

3. 选择合适的C值对于模型的性能至关重要。在实际应用中，我们需要根据具体的任务和数据集来选择合适的C值，以平衡模型的复杂度和拟合程度。通常可以通过交叉验证等方法来选择最优的C值。