一.波兰表达式（后缀表达式）

一个表达式E的后缀形式可以如下定义：
如果E是一个变量或常量，则E的后缀式是E本身。
如果E是E1 op E2形式的表达式，这里op是任何二元操作符，则E的后缀式为E1’E2’ op，这里E1’和E2’分别为E1和E2的后缀式。
如果E是（E1）形式的表达式，则E1的后缀式就是E的后缀式。
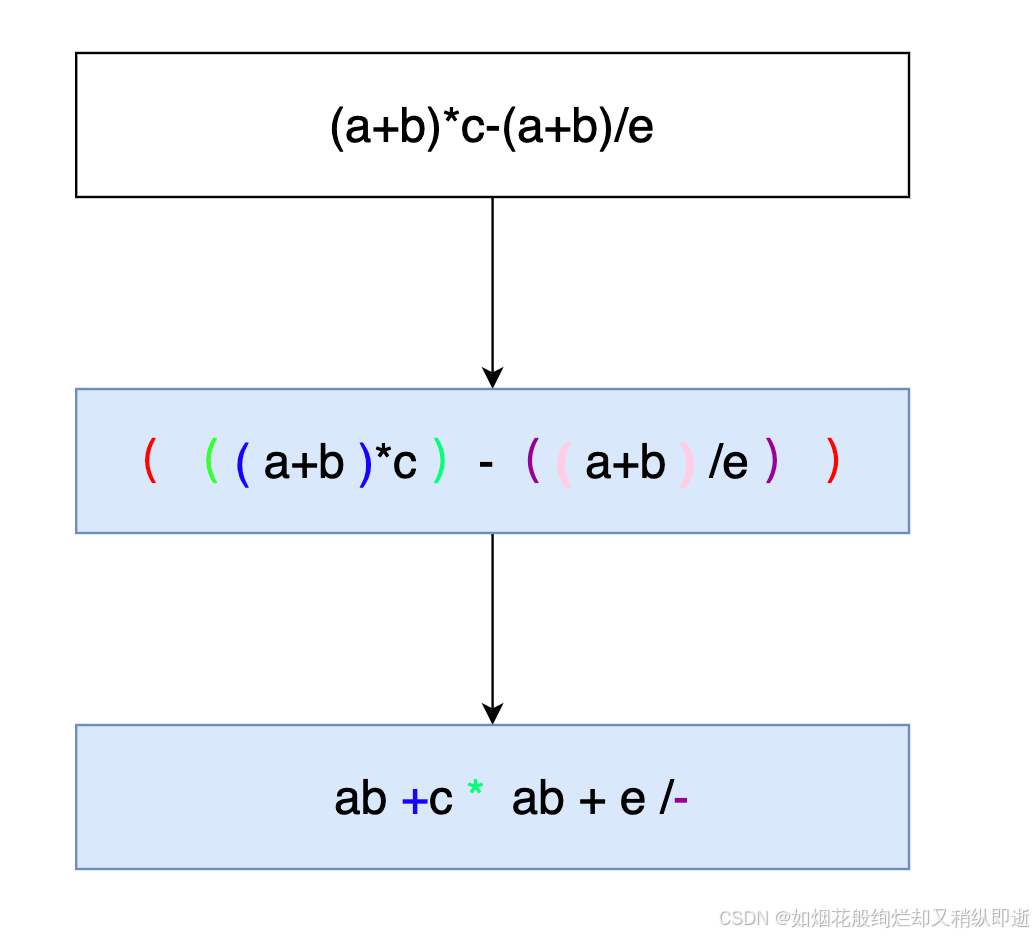
(a+b)c-(a+b)/e的后缀表达式为：
(a+b)c-(a+b)/e
→((a+b)c)((a+b)/e)-
→((a+b)c)((a+b)e/)-
→(ab+c)(ab+e/)-
→ab+cab+e/-
*我们将其中缀式的中每一个括号内对应的符号位置放到括号外去形成后缀表达式

对计算机而言中缀表达式是非常复杂的结构。相对来说，逆波兰式在计算机看来却是比较简单易懂的结构。因为计算机普遍采用的内存结构是栈式结构，它执行先进后出的顺序。*

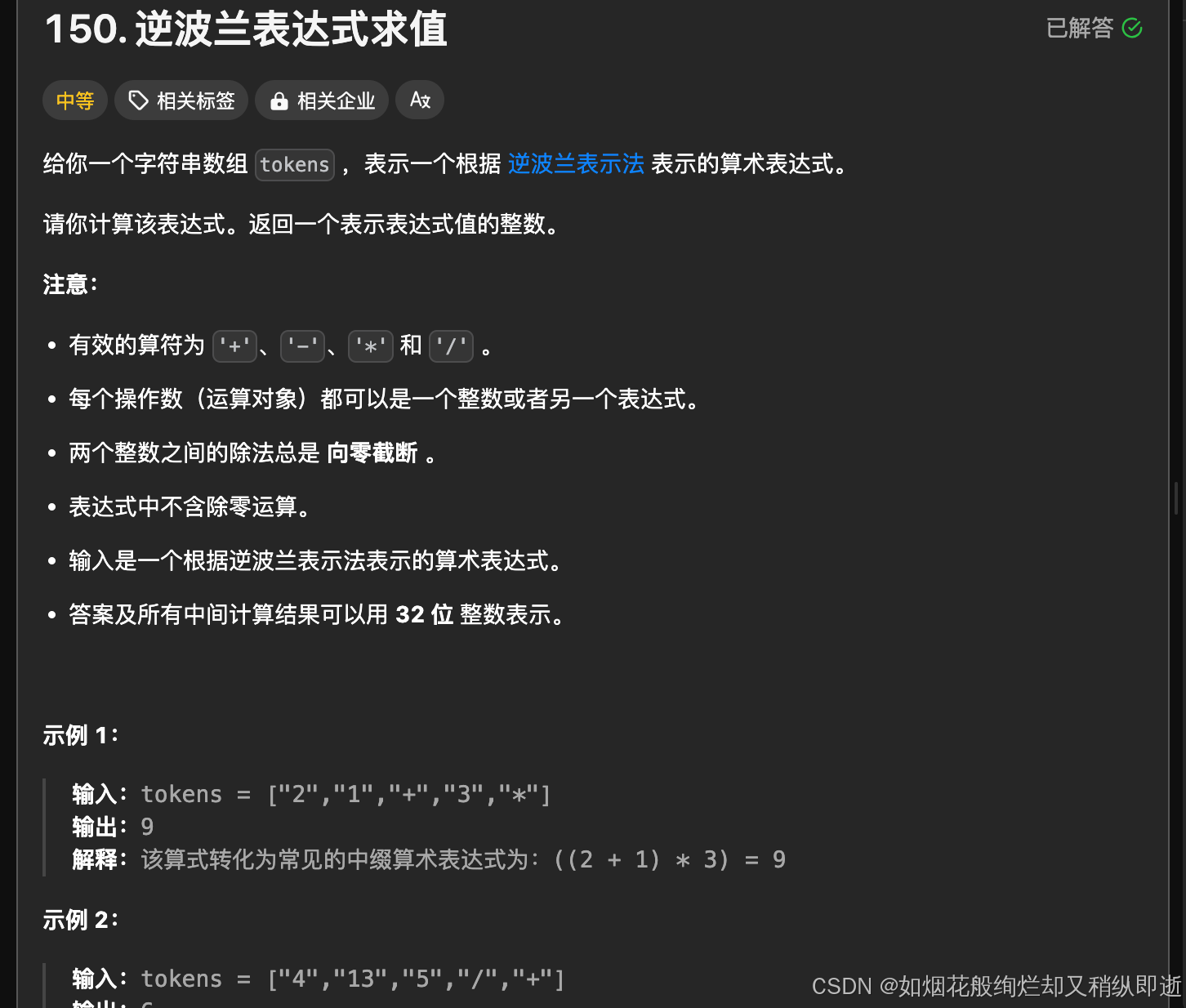
逆波兰表达式求值

class Solution {
 public int evalRPN(String[] tokens) {
        Stack<Integer> stack=new Stack<>();//定义栈存储
    for(String i:tokens){
        switch(i){
            case "+":
            Integer a =stack.pop();
            Integer b =stack.pop();
            stack.push(b+a);
            break;
            case "-":
             a =stack.pop();
             b =stack.pop();
            stack.push(b-a);
            break;
            case "*":
             a =stack.pop();
            b =stack.pop();
            stack.push(b*a);
            break;
            case "/":
             a =stack.pop();
             b =stack.pop();
            stack.push(b/a);
            break;
            default:
            stack.push(Integer.parseInt(i));//将它转为整数类型
            break;
        }
    }
   return stack.pop();//最终返回栈顶
}
}

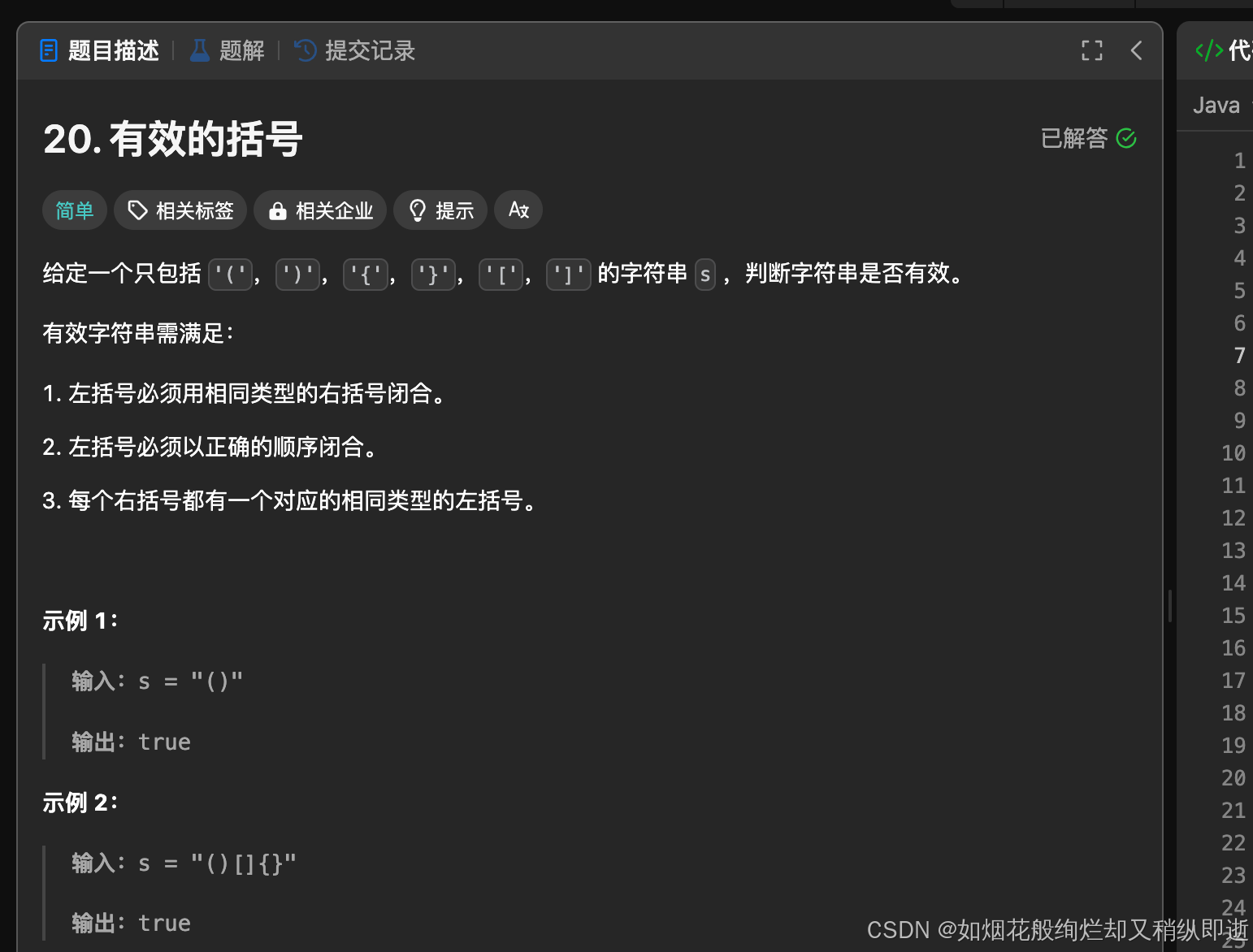
二.有效的括号

条件一需以相应的右括号闭合
条件二左括号和右括号的顺序需保持正确
条件三每个右括号都需要包含相同类型的左括号

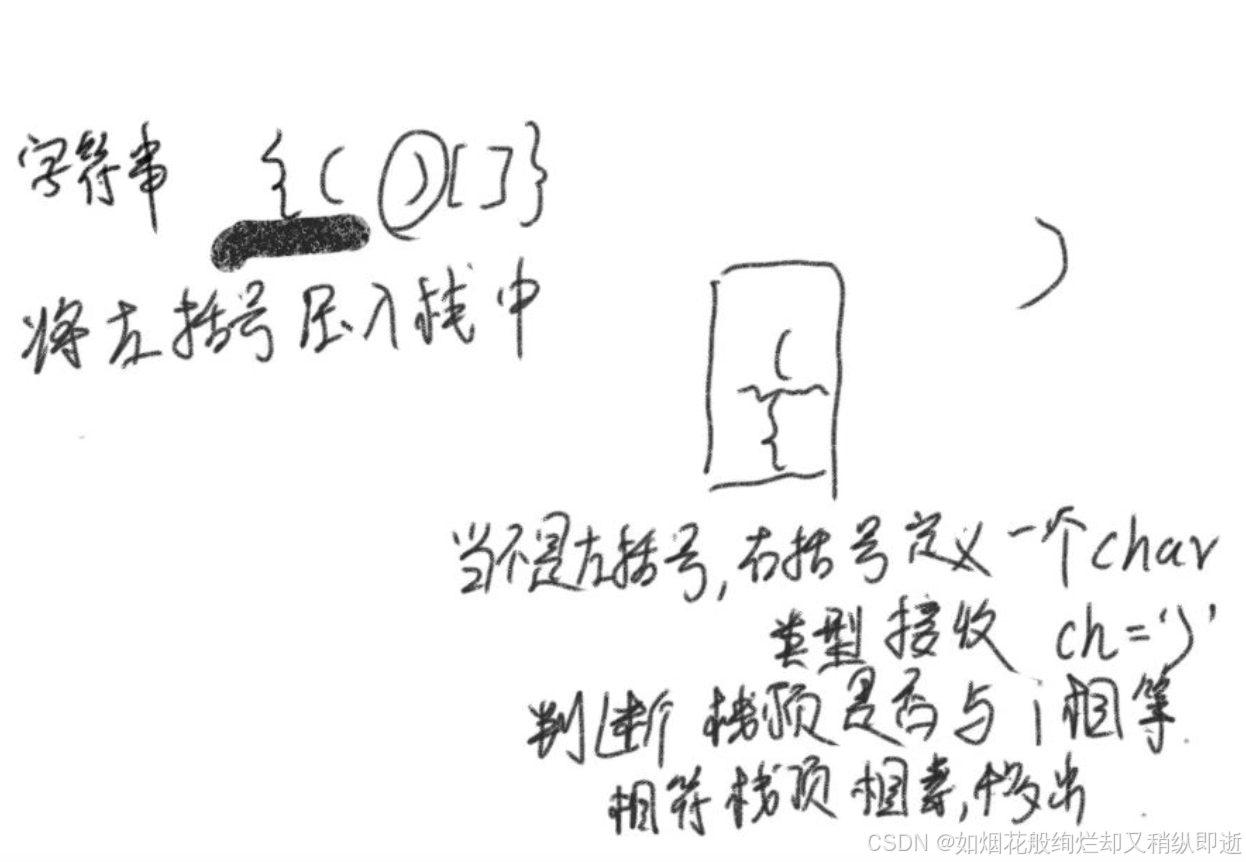
字有点丑…

   public boolean isValid(String s) {
       Stack<Character> stack=new Stack<>();
       int i=0;
       while(i<s.length()){
        char ch=s.charAt(i);
        if(ch=='{'||ch=='('||ch=='['){//判断是否为左括号
            stack.push(ch);//是的话放入栈中
        }else{//不是左括号
                if(stack.empty()){
                    //说明目前只有右括号
                    return false;
                }
                char ch2=stack.peek();//查看一个栈顶的符号是我们要找的左括号
                if(ch=='}'&&ch2=='{' ||  ch==')'&&ch2=='(' || ch==']'&&ch2=='['){
                    //进入循环说明ch为右括号，ch2获取到左括号进行匹配
                    stack.pop();//将栈顶元素清除
                }else{
                   return false;
                }
        }
        i++;
       }
       //如果循环出来后栈中仍然有元素说明没有可以匹配的
       if(!stack.empty())return false;
       return true;
    }

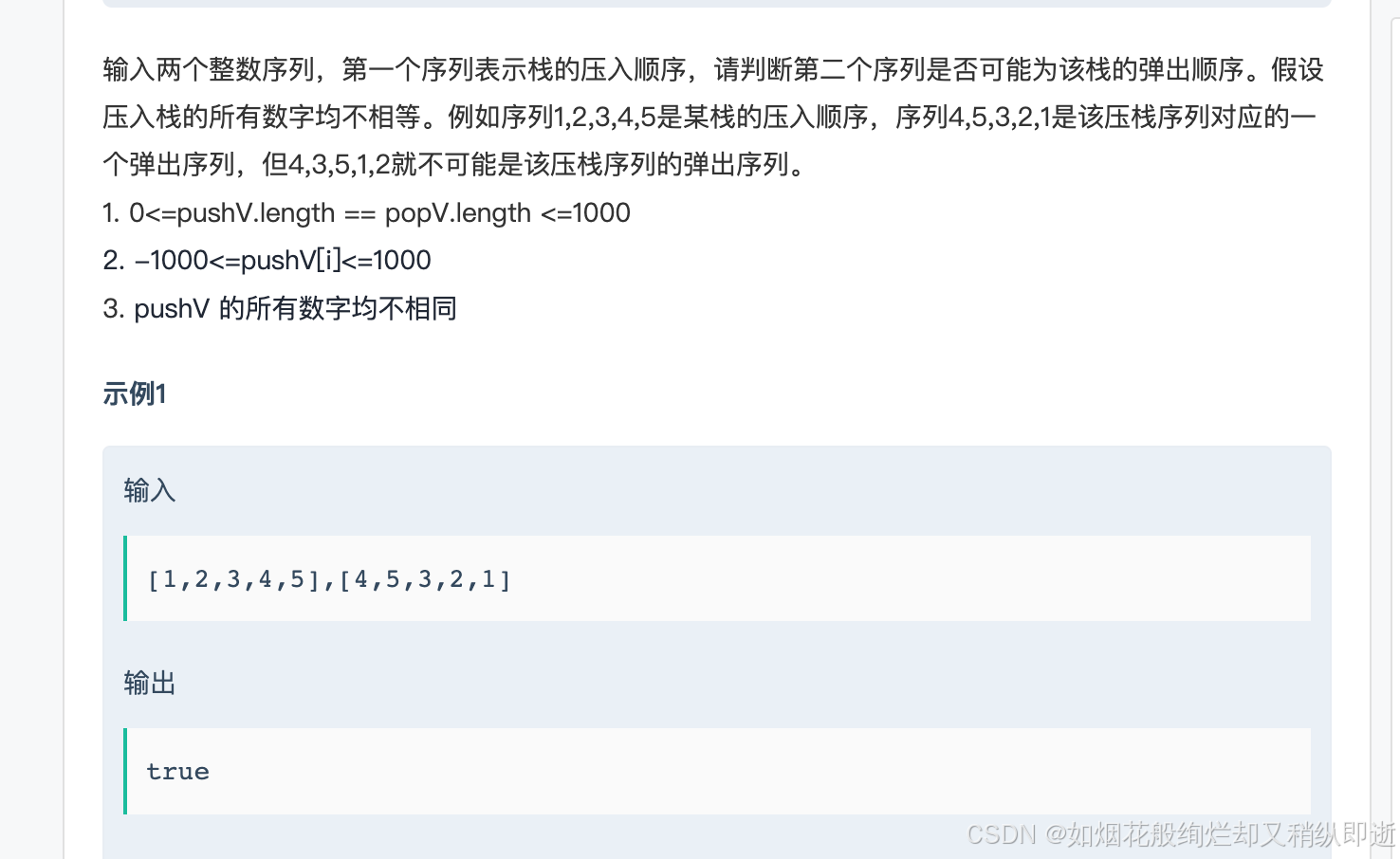
三.栈的压入、弹出序列

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param pushV int整型一维数组
     * @param popV int整型一维数组
     * @return bool布尔型
     */
    public boolean IsPopOrder (int[] pushV, int[] popV) {
        // write code here
        Stack<Integer>stack = new Stack<>();
        int j = 0;
        for (int i = 0; i < pushV.length; i++) {
            stack.push(pushV[i]);//首先将push中的数据放入栈中
            //设置一个循环j来遍历popV数组并且popV[j]与val匹配并且栈中有元素
            while (!stack.empty() && j < popV.length && popV[j] == stack.peek()) {
                stack.pop();
                j++;
            }
        }
        return stack.empty();
    }
} 

四.最小栈

 private Stack<Integer> stack;
        private Stack<Integer> minstack;
    public MinStack() {
        //初始化
         stack=new Stack<>();
        minstack=new Stack<>();
    }
    public void push(int val) {
        if(stack.empty()){//栈为空放入元素
            stack.push(val);
            minstack.push(val);
        }else{//不为空进行判断
            stack.push(val);//栈一始终放入元素进去
            int elem=stack.peek();//查看栈顶元素并接收
            if(elem<=minstack.peek()){//这里不排除有相同的元素
                minstack.push(elem);
            }
        }
    }
    
    public void pop() {
        if(stack.empty()||minstack.empty()){
        //1栈2栈为空
            return;
        }
        int val=stack.pop();
        //将val值与2栈顶比较想等删除
        if(val==minstack.peek()){
            minstack.pop();
        }
    }
    
    public int top() {
        if(stack.empty()){
            return -1;
        }
        return stack.peek();
    }
    
    public int getMin() {
        if(minstack.empty()){
            return -1;
        }
        return minstack.peek();
    }