程序员在程序设计时常常需要对存储在数组中的大量数据进行处理,如排序、查找等。使用数据库时,用户可能需要频繁通过输入键字值来查找相应的记录。在数组中搜索一个特定元素的处理过程,称为查找。上次我们已经介绍了一种最基础的查找算法——线性查找(顺序查找)这次我们来介绍一种查找算法:折半查找。
我们知道,线性查找法不要求被查找的数组元素事先是有序排列的,所以既可能在第一个元素位置,也可能在最后一个元素位置,找到与查找键相等的元素值。
然而在日常生活的很多场合下需要在有序条件下进行检索操作,例如电话簿中的姓名、字典、图书馆或书架上的书、邮递员包裹里的信件、班级名册、地址簿、计算机中的文件列表等,在有序表中查找信息比较容易,如果信息列表(例如价格表)是有序的,一些特殊数字(如最大和最小值)就会很显眼,因为它们会位于列表的开头或末尾,重复的数字也容易发现,因为它们都是相邻的。
当待查找信息有序排列时,折半查找法比顺序查找法的平均查找速度要快得多。折半查找也成为对分搜索。二分法求方程的根使用的也是对分搜索的思想,正如二分法要求在求根区间中函数是单调的一样,使用折半查找法的前提是被查找的数据集合是已排好序的。顺序查找法不受这一前提条件的约束,所以对于无序的数据而言,顺序查找是唯一可行的办法。
折半查找法的基本思想为:首选选取位于数组中间的元素,将其与查找键进行比较。如果它们的值相等,则查找键被找到,返回数组中间元素的下标,否则,将查找的区间缩小为原来区间的一半,即在一半的数组元素中查找。假设数组元素已按升序排列,如果查找键小于数组的中间元素值,则在前一半数组元素中继续查找,否则在后一半数组元素中继续查找。如果在该子数组(原数组的一个片段)中仍未找到查找键,则算法将在原数组的四分之一大小的子数组中继续查找。每次比较之后,都将目标数组中一半的元素排除在比较范围之外。不断重复这样的查找过程,直到查找键等于某个子数组中间元素的值(找到查找键),或者子数组只包含一个不等于查找键的元素(即没有找到查找键为止)。
听起来很抽象,难以理解?我们先来玩一个猜数游戏:我在1到100之间随便想一个整数,你来猜数,当你猜错的时候,我会提醒你猜的数是过大还是过小。
首先,我相信你的第一选择是50,这样能够把1~100分成1~49和51~100两个区间,如果我提示过大,你就能在1~49之间再猜一个数,这样猜中的几率就从1%变成了2%,提高了一倍(当然如果一次猜中那就是欧皇了)……接下来反复重复这个步骤,直到猜中为止,最多只需要猜6~7次就能把数猜出来。其实我们在不知不觉中已经运用了折半查找的思想。
理论上说,折半查找最多所需的比较次数是第一个大于数组元素个数的2的幂次数。以查找一个拥有1024个元素的数组为例,采用折半查找,在最坏的情况下只需10次比较。因为不断地用2来除1024得到的商分别是512、256、128、64、32、16、8、4、2、1,即1024(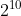
因此我们在查找数据时,如果能先使用排序算法对数据进行排序,再对数据进行折半查找,就能够大大提高我们的效率。鉴于排序算法在我之前的文章中已有提及,这里不再赘述:C语言丨交换法排序、C语言丨选择法排序、C语言丨冒泡法排序
假如我们有22 24 26 28 30五个数据,查找值x=28,我们可以先把第一个元素22的下标设置为low,最后一个元素30的下标设置为high,则中间的元素的下标mid=low+(high-low)/2(若使用mid=(high+low)/2计算mid的值,如果使用数组长度很大很大,使得low和high之和超出了limits.h中定义的有符号整数的极限值,那么执行到取数据区间中点的语句“mid=(high+low)/2;”时就会发生数值溢出,导致mid成为负数),那么我们查找的过程可展现如下:
| 数组下标 | 0 | 1 | 2 | 3 | 4 | |
| 第一次循环 | 22 | 24 | 26 | 28 | 30 | 查找值x=28 |
| low | mid | high | x>array[mid],low=mid+1 | |||
| 第二次循环 | 22 | 24 | 26 | 28 | 30 | |
| low(mid) | high | x=array[mid],找到 |
若查找值x=27,则查找过程如下:
| 第一次循环 | 22 | 24 | 26 | 28 | 30 | 查找值x=27 |
| low | mid | high | x>array[mid],low=mid+1 | |||
| 第二次循环 | 22 | 24 | 26 | 28 | 30 | |
| low(mid) | high | x<array[mid],high=mid-1 | ||||
| 第三次循环 | 22 | 24 | 26 | 28 | 30 | 不满足low<=high |
| high | low | 循环结束,未找到 |
按此算法编写折半查找函数BinSearch()如下:
//按折半查找法查找值为x的数组元素,若找到则返回x在数组中的下标位置,否则返回-1
int BinSearch(int array[], int x, int n)
{
int low = 0, high = n-1, mid;//区间左端点low置为0,右端点high置为n-1
while (low <= high)//若左端点小于等于右端点,则继续查找
{
mid = low + (high - low) / 2;//取数据区间的重点
if (x > array[mid])
low = mid + 1;//若x>array[mid],则修改区间的左端点
else if (x < array[mid])
high = mid - 1;//若x<array[mid],则修改区间的右端点
else
return mid;//若找到,则返回下标值mid
}
return -1;//循环结束仍未找到,则返回值-1
}以上程序是按待查找数据已按升序排列而写的;若待查找顺序已按降序排列,只需将if与else if语句中的大于号和小于号互换即可。
同理,若要查找的元素为字符串,只需适当修改判断语句即可,详情可参考C语言丨线性查找(顺序查找)
相对于线性查找而言,折半查找算法稍微复杂一些,但效率很高,当数据量非常大时,使用这种方法无疑可以让我们事半功倍。
参考文献:
苏小红 赵玲玲 孙志岗 王宇颖 等编著 蒋宗礼 主审,C语言程序设计(第4版),高等教育出版社,P210,P212-215.