C语言丨线性表（二）：线性链表（单链表）

线性表是由数据类型相同的 $n\left ( n\geq 0 \right )$ 个数据元素组成的有限序列，通常记为：

$\left ( a_{1},a_{2},\cdots ,a_{i-1},a_{i},a_{i+1},\cdots ,a_{n} \right )$

其中n为表长，n=0时称为空表；下标i表示数据元素的位序。

线性表的特点是组成它的数据元素之间是一种线性关系，即数据元素“一个接在另一个的后面排列，每一个数据元素的前面和后面都至多有一个其他数据元素”。

本文在介绍线性表的基本概念的基础上，重点介绍线性链表（单链表）及相应的算法。

定义

链表是通过一组任意的存储单元来存储线性表中的数据元素，每一个结点包含两个域：存放数据元素信息的域称为数据域，存放其后继元素地址的域称为指针域。因此n个元素的线性表通过每个结点的指针域连接成了一个“链条”，称为链表。若此链表的每个结点中只包含一个指针域，则被称为线性链表或单链表。

线性表的链式存储结构，它不需要用地址连续的存储单元来实现，因为它不要求逻辑上相邻的两个数据元素物理位置上也相邻，它是通过“指针”建立起数据元素之间的逻辑关系。

链表是由一个个结点构成的，结点定义如下：

typedef struct node
{
    DataType data;
    struct node *next;
} Linklist;

线性链表的存取必须从表头指针开始，表头指针指示线性链表中第一个结点的存储单位置。由于线性表最后一个数据元素没有直接后继，则线性链表中的最后一个结点的指针域为“空”（NULL）。

为了使用方便可以在第一个元素的前面增加一个结点（被称为头节点），该节点的数据域为空，指针域中存储线性链表的第一个元素所在的结点（表头结点）的存储地址。如果为空表，则指针域为空。

因此空链表也分为带有头结点的空链表和不带头结点的空链表。若有头结点，头结点的数据域为空，指针域为空，则说明该链表为空链表；若没有头结点，表头指针为空指针，则说明该链表为空链表。

1.插入

假设要在线性表的两个数据元素a和b之间插入一个数据元素x，p为指向结点a的指针。为了插入数据元素x，首先要生成一个数据域为x的新结点，s为指向新增节点的指针，然后使新增节点的指针域指向b(p->next)，结点a的指针域指向新增节点(s)。

int InsertLinkList(LinkList *H, int i, DataType x)
/*在有头结点的线性链表H中第i个位置前插入元素x*/
{
    LinkList *p;
    LinkList *s;
    int j = 0;
    p = H;
    while (p && j<i-1)
    {
        p = p->next;
        j++;
    }/*循环直到p指向第i-1个元素*/
    if (!p)
        return -1;/*i大于表长加1*/
    s = (LinkList *)malloc(sizeof(LinkList));
    s->data = x;
    s->next = p->next;/*插入数据元素x*/
    p->next = s;
    return 1;
}

2.建立线性链表

1)头插法

建立线性链表应从空表开始，每读入一个数据元素则申请一个结点，然后插在链表的头结点与第一个结点之间。记头结点为H，申请的结点为s，按照上述插入算法，操作步骤为：

s->next = H->next; H->next = s;

再加上新建头结点、读入数据元素、申请结点等步骤，可编程如下：

LinkList *CreateLinkList_front()
{
    LinkList *H;/*H表示头结点*/
    LinkList *s;
    char x;/*设数据元素的类型为char*/
    H = (LinkList *)malloc(sizeof(LinkList));/*为头结点申请内存空间*/
    H->next = NULL;
    scanf(" %c", &x);
    while (x!=flag)/*flag为结束创建过程的标志，如'#'等*/
    {
        s = (LinkList *)malloc(sizeof(LinkList));
        s->data = x;
        s->next = H->next;
        H->next = s;
        scanf(" %c", &x);
    }
    return H;
}

因为是在链表的头部插入，读入数据的顺序和线性表中的逻辑顺序是相反的。

2)尾插法

在表头插入建立线性链表方法简单，但读入数据元素的顺序与生成的链表中元素的顺序是相反的，若希望次序一致，则用尾插法。因为每次是将新结点插入到链表的尾部，所以需加入一个指针用来始终指向链表中的尾结点，以便能够将新结点插入到链表的尾部。

在前面，我们介绍了插入算法，在这里可以通过调用插入算法，即定义一个变量int i = 1;，调用前面的函数InsertLinkList(H, i, x);，每插入一个数据元素，便使i++;，这样就可一直保持在链表的尾部插入。

LinkList *CreateLinkList_rear()
{
    LinkList *H;
    DataType x;/*设DataType为数据元素的类型*/
    int i = 1;
    H = (LinkList *)malloc(sizeof(LinkList));
    H->next = NULL;
    scanf(&x);/*读入数据元素的值*/
    while (x!=flag)
    {
        InsertLinkList(H, i, x);/*调用插入算法*/
        i++;
        scanf(&x);
    }
    return H;
}

但是这样使得算法的时间复杂度比头插法要高出了一个数量级，因为每次在尾部插入数据元素时，都要重新调用InsertLinkList()函数，使指针重新从表头指针开始指向尾结点。

因此我们可以使指针（记为p）一直指向链表中的尾结点，然后让新结点（记为s）按照插入算法插入链表的尾部。只需修改上述代码的while循环即可实现：

LinkList *CreateLinkList_rear()
{
    LinkList *H, *p, *s;
    DataType x;/*设DataType为数据元素的类型*/
    H = (LinkList *)malloc(sizeof(LinkList));
    H->next = NULL;
    scanf(&x);/*读入数据元素的值*/
    p = H;
    while (x!=flag)
    {
        s = (LinkList *)malloc(sizeof(LinkList));
        s->data = x;
        s->next = NULL;
        p->next = s;
        p = p->next;
        scanf(&x);
    }
    return H;
}

3.删除

假设链表中有a, b, c3个数据元素，要删除数据元素a和数据元素c中间的数据元素b时，仅需修改数据元素a所在的结点的指针域。假设指针p指向数据元素a，用语句表示就是：

p->next = p->next->next;

添加一个指针变量q，让q指向数据元素b，当改变数据元素a所在的结点的指针域后，即可释放q的内存，即释放数据元素b所占的内存。进一步地，调用函数时传入标志变量i，可实现删除第i个数据元素。

int DeleteLinkList(LinkList *H, int i)
/*在有头结点的线性链表H中删除第i个元素*/
{
    LinkList *p;
    LinkList *q;
    int j = 0;
    p = H;
    while (p->next && j<i-1)
    {
        p = p->next;
        j++;
    }/*循环直到p指向第i-1个元素*/
    if (!(p->next))
        return -1;/*删除节点不合法*/
    q = p->next;
    p->next = q->next;/*删除第i个数据元素*/
    free(q);/*释放第i个数据元素所占内存*/
    return 1;
}

对比插入算法和删除算法，while循环的功能同样是使p指向第i-1个元素，为什么插入算法的循环条件为p && j<i-1，而删除算法的循环条件是p->next && j<i-1？能否将删除算法的循环条件也改为p && j<i-1？

这是因为，在链表根本没有i-1个元素的情况下，循环条件为p && j<i-1的循环运行结果为p指向尾结点的下一个结点即p=NULL，而循环条件为p->next && j<i-1的循环运行结果为p指向尾结点即p≠NULL。若将删除算法的循环条件也改为p && j<i-1，在链表根本没有i-1个元素的情况下，while循环后面的语句if (!(p->next))将会造成非法内存访问，因为此时p=NULL，我们无法访问空指针指向的内容。

4.查找

查找结点使用的算法是线性查找法（顺序查找法），即从链表的第一个结点开始，顺着指针链一个一个比较，相等则查找成功，返回结点位置；如果比较到最后也没有相等的，则查找不成功，返回空。

LinkList *SearchLinkList(LinkList *H, DataType x)
/*在线性链表H中查找值为x的结点，找到后返回其指针，否则返回空*/
{
    LinkList *p = H->next;/*p指向线性链表的第一个数据元素*/
    while (p!=NULL && p->data!=x)
        p = p->next;
    return p;
}

若要返回值为x的结点在链表中的位序，则可使用一个标记变量i，记录结点的位序；若找不到则返回-1。修改程序如下：

int SearchLinkList(LinkList *H, DataType x)
/*在线性链表H中查找值为x的结点，找到后返回其在链表中的位序，否则返回-1*/
{
    LinkList *p = H->next;/*p指向线性链表的第一个数据元素*/
    int i = 1;
    while (p!=NULL && p->data!=x)
    {
        p = p->next;
        i++;
    }
    if (p != NULL)
        return i;
    else
        return -1;
}

5.求线性链表的表长

设H是带头结点的线性链表（线性表的长度不包括头结点），求线性链表的表长的操作与上述查找某结点在链表中的位序相似。

int LinkListLength(LinkList *H)
{
    LinkList *p = H;/*p指向头结点*/
    int n = 0;
    while (p->next)
    {
        p = p->next;
        n++;
    }/*p所指的是第n个结点*/
    return n;
}

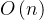
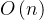
可以证明，上述算法的平均时间复杂度都为 $O\left ( n \right )$ 。在上一篇文章C语言丨线性表（一）：顺序表中也讲到，顺序表的基本运算算法的平均时间复杂度也为 $O\left ( n \right )$ 。

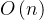
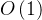
既然顺序表和链式表的基本运算算法的平均时间复杂度都为 $O\left ( n \right )$ ，那么我们该如何进行选择呢？我们主要从空间和时间两个角度考虑。线性表的链式存储结构适用于程序中使用到的线性表的长度变化很大的情形，而当线性表的长度变化不大且易于事先确定大小时，宜采用顺序表。另外，顺序表是随机存取结构，对表中任何结点都可在 $O\left ( 1 \right )$ 时间内直接地存取，而链式表中的结点，需从头指针起顺着链扫描才能取到。因此，若主要是进行查找操作，则宜采用顺序表；但若需要频繁进行插入和删除操作，由于对于线性表来说要大量挪动元素，而链式表只需要修改指针，此时宜采用链式表。

参考文献：

文益民张瑞霞李健编著，数据结构与算法（第2版），清华大学出版社，P18，P25-31.