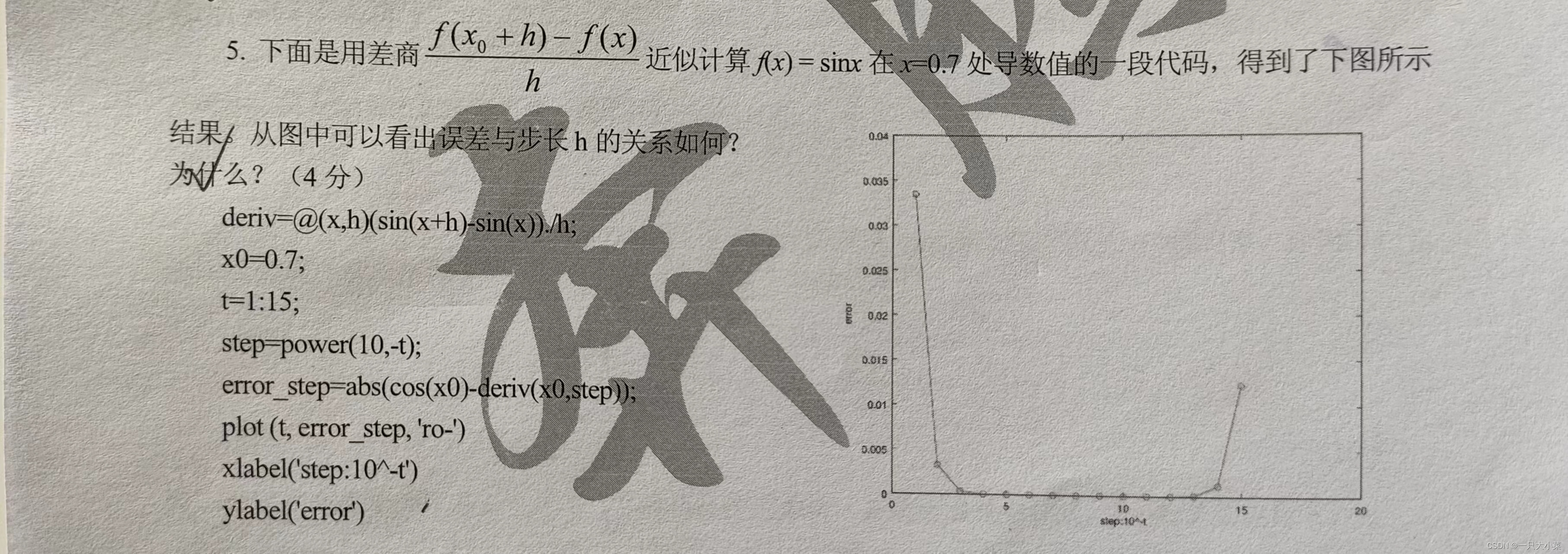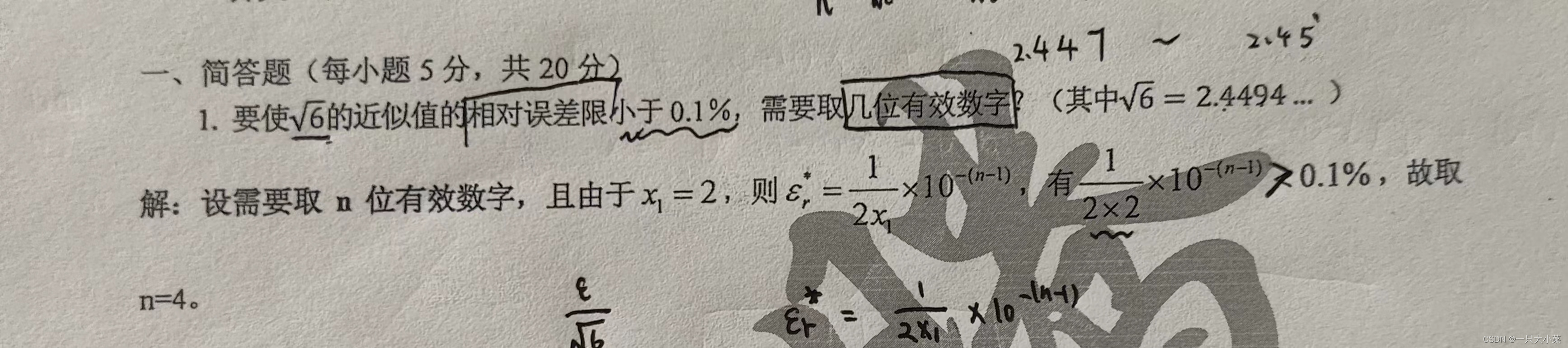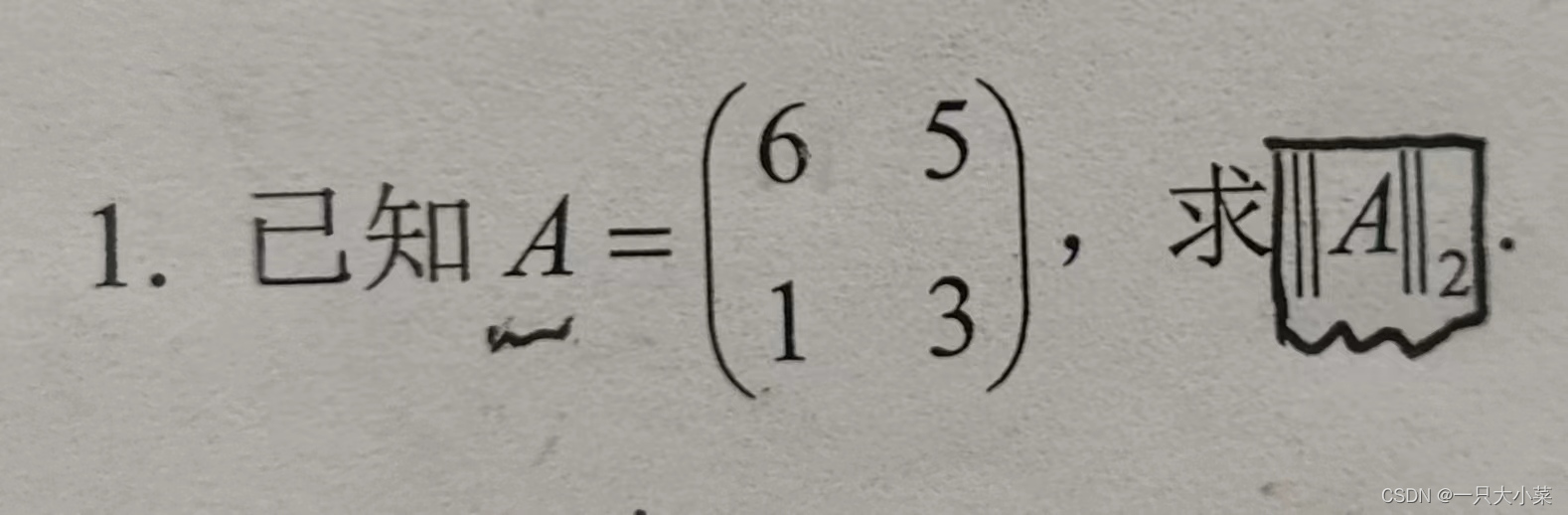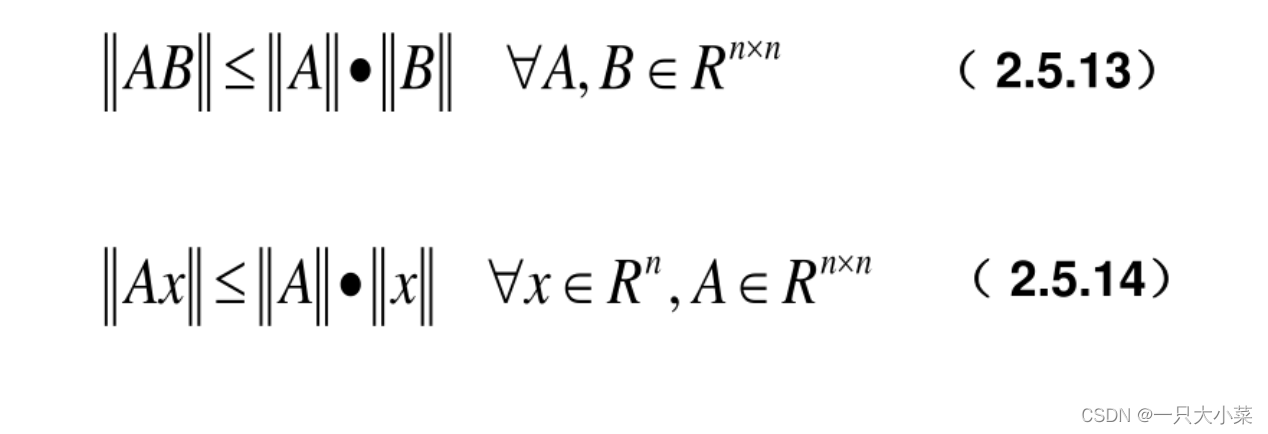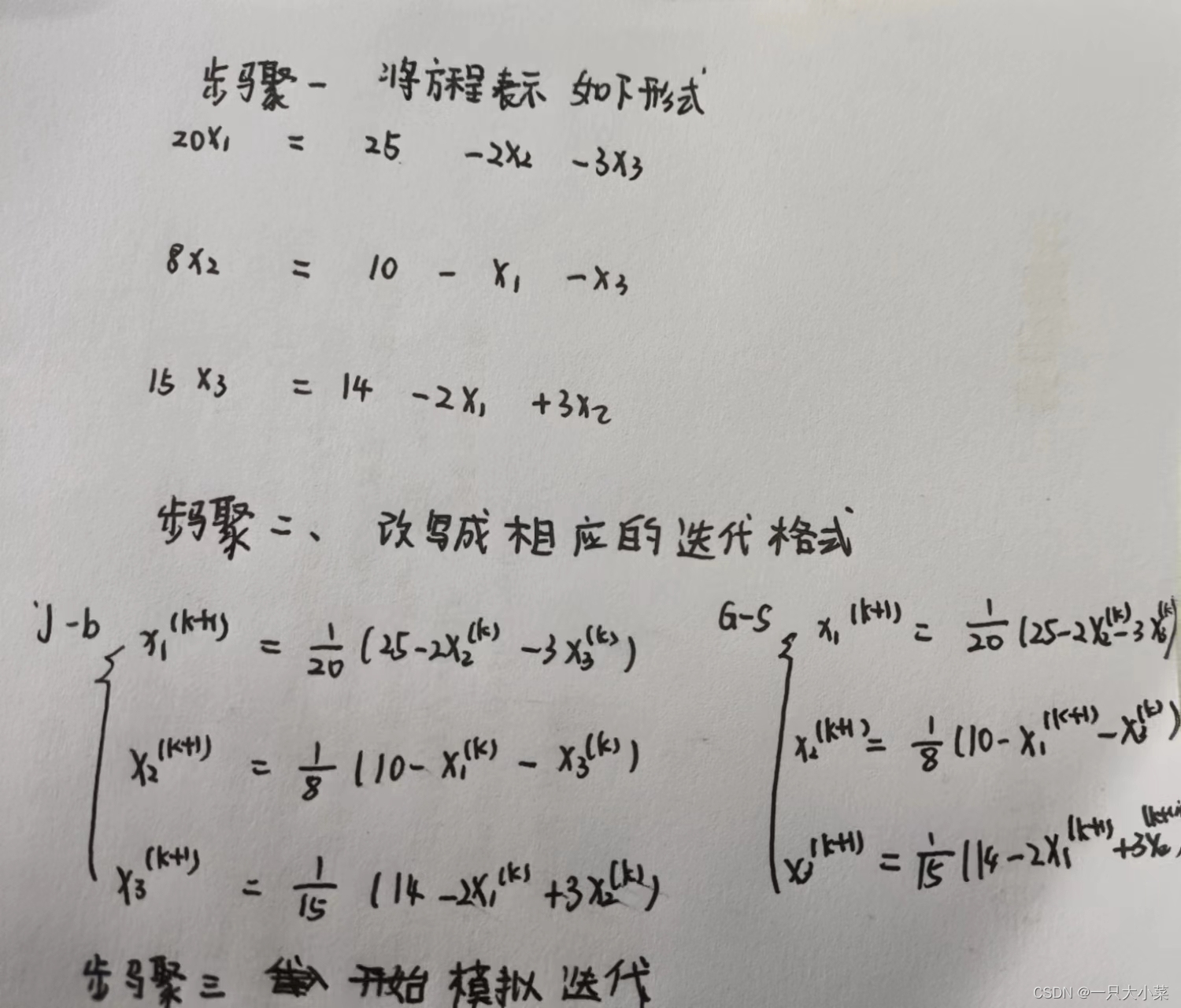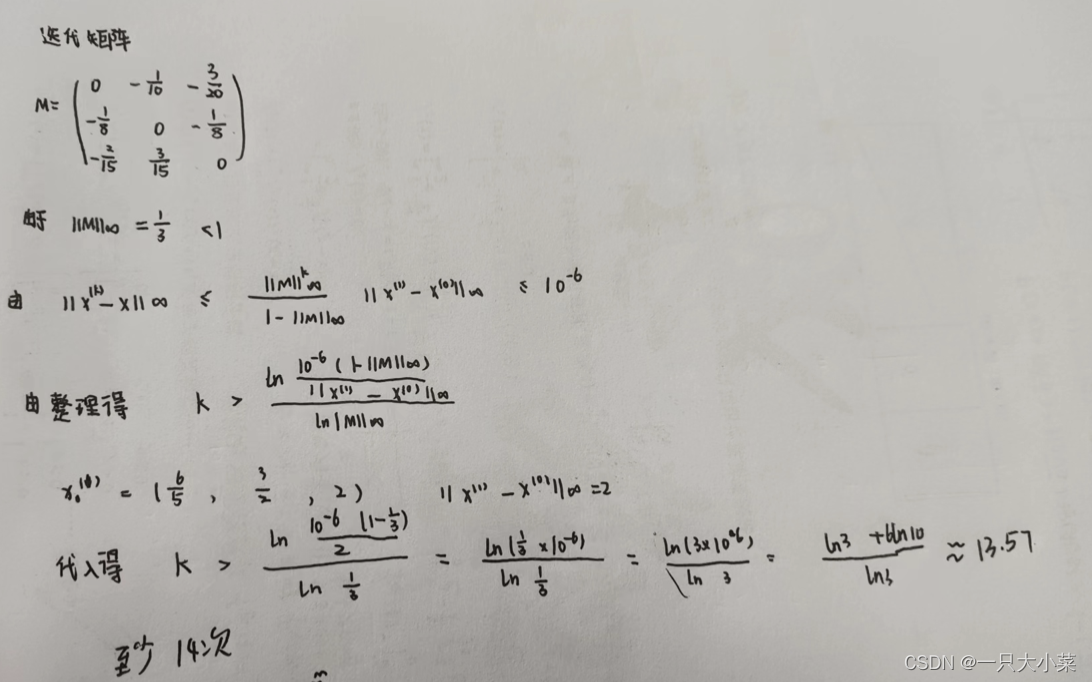0. 知识点范围及例题来源

知识点范围来自时老师的ppt，例题来源于历年考试真题以及日常作业题。

1. 绪论

1.1 浮点数的四则运算

在计算机中实数采用二进制浮点系统进行表示的，因此只能表示出有限的离散点，每个实数均由该集合中距离其最近的点近似表示，也即有舍入误差。而0.25恰好被包含在离散点中因此舍入误差为0，而0.2不在该集合中，因此对0.2的表示出现舍入误差。

1.2 误差的来源

从图中可以看出在开始阶段，随着步长的减小误差不断减小，但是当误差减小到一定程度时误差反而呈现上升趋势

在初始阶段，误差主要体现在方法误差，随着h的减小误差减小，当误差减小到一定程度时，舍入误差越来越大，导致后期的误差变大。

1.3 绝对误差 相对误差 有效数字

1.4 误差分析

2. 解线性方程组的数值法

2.1 消元法

高斯消元算法的主元素选取思想是将系数绝对值最大的元素作为主元素，然后通过行交换操作把该主元素移到当前行的对角线位置上。这样选取主元素的优点是可以尽可能地避免舍入误差和数值不稳定性问题，从而得到更加准确和可靠的解。一般有列主元和全主元两种选取主元的方式。

2.2 向量和矩阵范数

范数要满足三个条件： 正定性，齐次性，三角不等式

相容范数

2.3 迭代法

迭代格式 ： $x^{\ast }=M{x}^{\ast }+g$
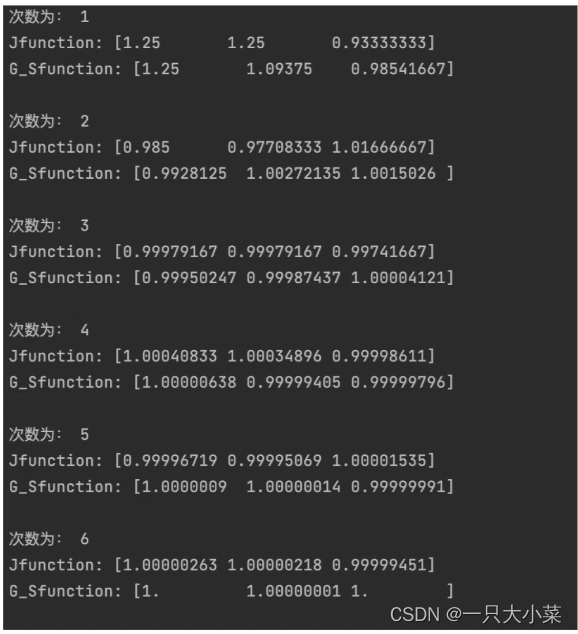
迭代的收敛性：

• $M^k->O$是迭代法收敛的充要条件
• $\rho (M)<1$ 是迭代矩阵的充要条件
• $||M||<1$ 是充分条件

太难算了，呜呜呜～～～

3 非线性方程组的数值解

3.1 不动点迭代法

3.2 牛顿迭代法

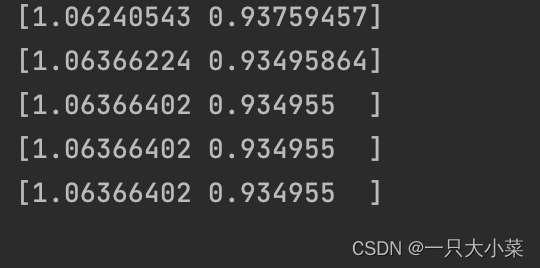
3.3 解非线性方程组的牛顿迭代法

这种题目考的可能性不是很大，因为太难算了,非人力所能及也。