参考:
fun-rec/docs/ch02/ch2.1/ch2.1.1/mf.md at master · datawhalechina/fun-rec · GitHub
业务
隐语义模型与矩阵分解
协同过滤算法的特点:
- 协同过滤算法的特点就是完全没有利用到物品本身或者是用户自身的属性, 仅仅利用了用户与物品的交互信息就可以实现推荐,是一个可解释性很强, 非常直观的模型。
- 但是也存在一些问题,处理稀疏矩阵的能力比较弱。
为了使得协同过滤更好处理稀疏矩阵问题, 增强泛化能力。从协同过滤中衍生出矩阵分解模型(Matrix Factorization, MF)或者叫隐语义模型:
- 在协同过滤共现矩阵的基础上, 使用更稠密的隐向量表示用户和物品。
- 通过挖掘用户和物品的隐含兴趣和隐含特征, 在一定程度上弥补协同过滤模型处理稀疏矩阵能力不足的问题。
近似最近邻查找
- 支持最近邻查找的系统
- 系统:Milvus、Faiss、HnswLib、等等
- 快速最近邻查找的算法已经被集成到这些系统中
- 衡量最近邻的标准:
- 欧式距离最小(L2 距离)
- 向量内积最大(内积相似度)
- 矩阵补充用的就是内积相似度
- 向量夹角余弦最大(cosine 相似度)
- 最常用
- 对于不支持的系统:把所有向量作归一化(让它们的二范数等于 1),此时内积就等于余弦相似度
音乐评分实例
假设每个用户都有自己的听歌偏好, 比如用户 A 喜欢带有小清新的, 吉他伴奏的, 王菲的歌曲,如果一首歌正好是王菲唱的, 并且是吉他伴奏的小清新, 那么就可以将这首歌推荐给这个用户。 也就是说是小清新, 吉他伴奏, 王菲这些元素连接起了用户和歌曲。
当然每个用户对不同的元素偏好不同, 每首歌包含的元素也不一样, 所以我们就希望找到下面的两个矩阵:
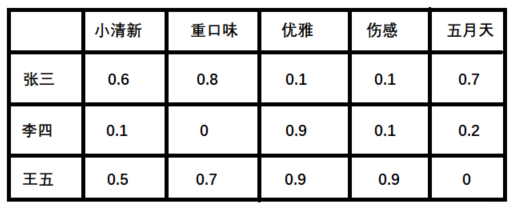
- 潜在因子—— 用户矩阵Q 这个矩阵表示不同用户对于不同元素的偏好程度, 1代表很喜欢, 0代表不喜欢, 比如下面这样:
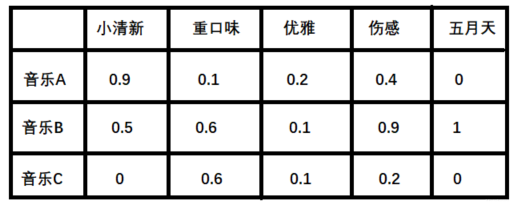
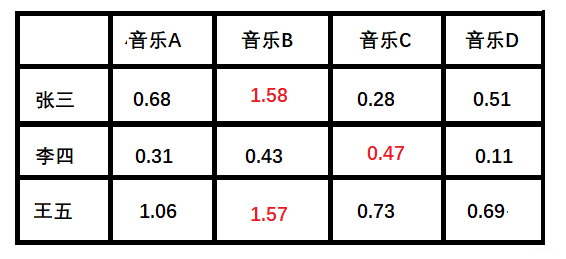
2. 潜在因子——音乐矩阵P 表示每种音乐含有各种元素的成分, 比如下表中, 音乐A是一个偏小清新的音乐, 含有小清新的Latent Factor的成分是0.9, 重口味的成分是0.1, 优雅成分0.2...
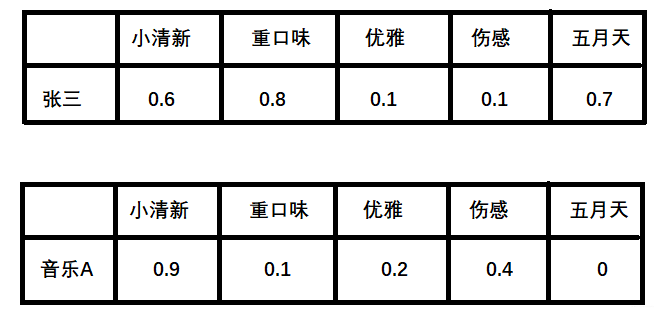
**计算张三对音乐A的喜爱程度**
利用上面的这两个矩阵,将对应向量进行内积计算,我们就能得出张三对音乐A的喜欢程度:
-
张三对小清新的偏好 * 音乐A含有小清新的成分 + 张三对重口味的偏好 * 音乐A含有重口味的成分 + 张三对优雅的偏好 * 音乐A含有优雅的成分...
-
根据隐向量其实就可以得到张三对音乐A的打分,使用内积相似度:
0.6∗0.9+0.8∗0.1+0.1∗0.2+0.1∗0.4+0.7∗0=0.680.6∗0.9+0.8∗0.1+0.1∗0.2+0.1∗0.4+0.7∗0=0.68
计算所有用户对不同音乐的喜爱程度
按照这个计算方式, 每个用户对每首歌其实都可以得到这样的分数, 最后就得到了我们的评分矩阵:
+ 红色部分表示用户没有打分,可以通过隐向量计算得到的。
小结
-
上面例子中的小清晰, 重口味, 优雅这些就可以看做是隐含特征, 而通过这个隐含特征就可以把用户的兴趣和音乐的进行一个分类, 其实就是找到了每个用户每个音乐的一个隐向量表达形式(与深度学习中的embedding等价)
-
这个隐向量就可以反映出用户的兴趣和物品的风格,并能将相似的物品推荐给相似的用户等。 有没有感觉到是把协同过滤算法进行了一种延伸, 把用户的相似性和物品的相似性通过了一个叫做隐向量的方式进行表达
-
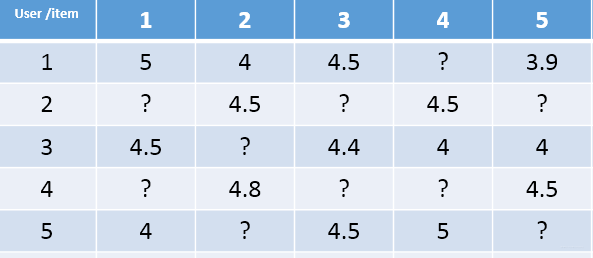
现实中,类似于上述的矩阵 P,QP,Q 一般很难获得。有的只是用户的评分矩阵,如下:
- 这种矩阵非常的稀疏,如果直接基于用户相似性或者物品相似性去填充这个矩阵是不太容易的。
- 并且很容易出现长尾问题, 而矩阵分解就可以比较容易的解决这个问题。
-
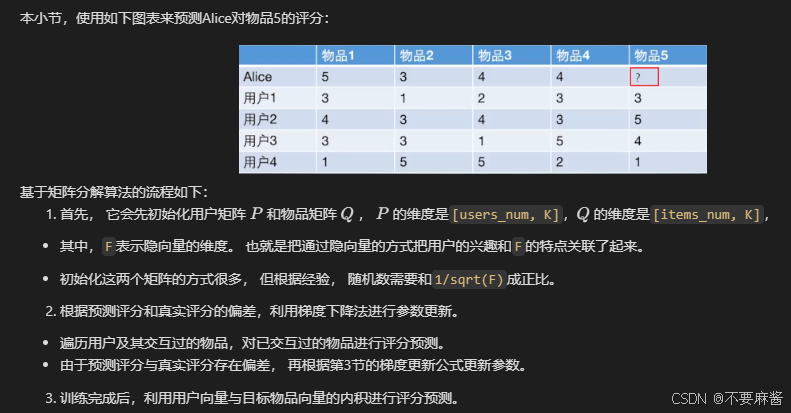
矩阵分解模型:
- 基于评分矩阵,将其分解成Q和P两个矩阵乘积的形式,获取用户兴趣和物品的隐向量表达。
- 然后,基于两个分解矩阵去预测某个用户对某个物品的评分了。
- 最后,基于预测评分去进行物品推荐。
编程实现
import random
import math
class BiasSVD():
def __init__(self, rating_data, F=5, alpha=0.1, lmbda=0.1, max_iter=100):
self.F = F # 这个表示隐向量的维度
self.P = dict() # 用户矩阵P 大小是[users_num, F]
self.Q = dict() # 物品矩阵Q 大小是[item_nums, F]
self.bu = dict() # 用户偏置系数
self.bi = dict() # 物品偏置系数
self.mu = 0 # 全局偏置系数
self.alpha = alpha # 学习率
self.lmbda = lmbda # 正则项系数
self.max_iter = max_iter # 最大迭代次数
self.rating_data = rating_data # 评分矩阵
for user, items in self.rating_data.items():
# 初始化矩阵P和Q, 随机数需要和1/sqrt(F)成正比
self.P[user] = [random.random() / math.sqrt(self.F) for x in range(0, F)]
self.bu[user] = 0
for item, rating in items.items():
if item not in self.Q:
self.Q[item] = [random.random() / math.sqrt(self.F) for x in range(0, F)]
self.bi[item] = 0
# 采用随机梯度下降的方式训练模型参数
def train(self):
cnt, mu_sum = 0, 0
for user, items in self.rating_data.items():
for item, rui in items.items():
mu_sum, cnt = mu_sum + rui, cnt + 1
self.mu = mu_sum / cnt
for step in range(self.max_iter):
# 遍历所有的用户及历史交互物品
for user, items in self.rating_data.items():
# 遍历历史交互物品
for item, rui in items.items():
rhat_ui = self.predict(user, item) # 评分预测
e_ui = rui - rhat_ui # 评分预测偏差
# 参数更新
self.bu[user] += self.alpha * (e_ui - self.lmbda * self.bu[user])
self.bi[item] += self.alpha * (e_ui - self.lmbda * self.bi[item])
for k in range(0, self.F):
self.P[user][k] += self.alpha * (e_ui * self.Q[item][k] - self.lmbda * self.P[user][k])
self.Q[item][k] += self.alpha * (e_ui * self.P[user][k] - self.lmbda * self.Q[item][k])
# 逐步降低学习率
self.alpha *= 0.1
# 评分预测
def predict(self, user, item):
return sum(self.P[user][f] * self.Q[item][f] for f in range(0, self.F)) + self.bu[user] + self.bi[
item] + self.mu
# 通过字典初始化训练样本,分别表示不同用户(1-5)对不同物品(A-E)的真实评分
def loadData():
rating_data={1: {'A': 5, 'B': 3, 'C': 4, 'D': 4},
2: {'A': 3, 'B': 1, 'C': 2, 'D': 3, 'E': 3},
3: {'A': 4, 'B': 3, 'C': 4, 'D': 3, 'E': 5},
4: {'A': 3, 'B': 3, 'C': 1, 'D': 5, 'E': 4},
5: {'A': 1, 'B': 5, 'C': 5, 'D': 2, 'E': 1}
}
return rating_data
# 加载数据
rating_data = loadData()
# 建立模型
basicsvd = BiasSVD(rating_data, F=10)
# 参数训练
basicsvd.train()
# 预测用户1对物品E的评分
for item in ['E']:
print(item, basicsvd.predict(1, item))
# 预测结果:E 3.685084274454321梯度下降推导