本文出自 AC.HASH团队,AC<=>Adaptive Creator,适应性创作者,旨在于能够在未来新领域下创造出新的哈希算法以应对未来局面。
产出本文的成员:
四名中原工学院大一在校生
我们是来自同一个班级的同学,我们在OpenHarmony成长计划啃论文俱乐部里,与华为、软通动力、润和软件、拓维信息、深开鸿等公司一起,学习和研究操作系统技术…
Table of Contents
【本期看点】
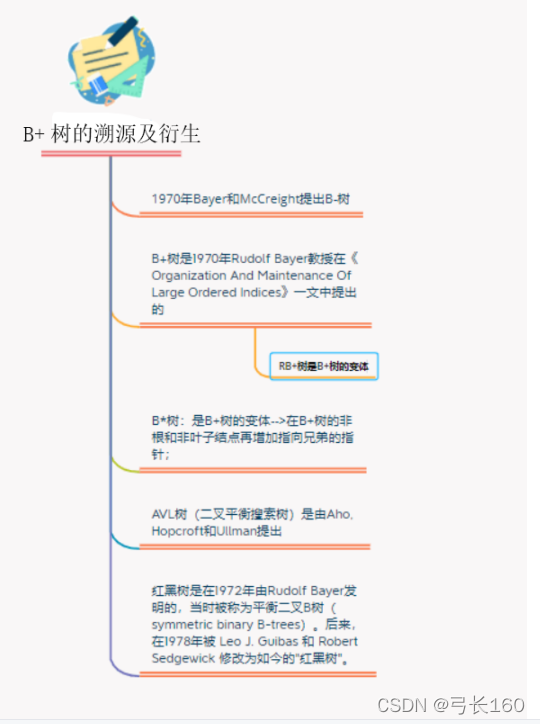
1.B+树的溯源及衍生。
2.B+树。
2.1 什么是B+树?
2.2 B+树有哪些特性?
2.3 B+的增删改查。
3.总结
4.参考文献
【本期看点】
主题:《老子到此一游系列》之 老子见证了B+树的沧海桑田。
B+树的溯源及衍生。
索引技术是提高海量数据查询效率的关键技术之一。为了应对如今错综复杂和海量的数据检索问题,其根本是数据的储存方式。因此数据的储存和查询在不断的更新换代。下面我们来介绍B+树相关的知识。
2.B+树
2.1 什么是B+树?
在搞懂什么是B+树之前。我们先介绍为什么要讲B+树?B+树是用来干啥的?为什么讲B+树,因为它在B树的基础之上存储的元素更多,减少了IO次数,更夯实了查询性能的稳定,而且将所有叶子节点形成有序链表,优化了范围查询。
想要短时间掌握其定义首先要知道B+树是一种用于数据库索引的数据结构,B + 树是一种多路搜索树,既然是树,想必其也少不了根,枝,页。在B+树中其分别命名为根节点、内部节点,叶子节点三类。
其官方定义为:一棵 m 阶的 B+树或者为空树或者满足以下特性:① 树中的每个节点最多有 m个子树。2. 根节点至少要有2个子树。③ 除根之外的非终端节点‚至少有[m/2] 个子树。 ④ 有 K 个子树的非叶节点恰好包含 K 个关键字。⑤ 所有的非叶子结点包含下列信息数据(P0‚K1‚P1‚ K2‚…‚Pn-1‚Kn)‚其中‚Ki(i =1‚2‚…‚n) 为关键字‚且 Ki < Ki+1;Pi(i =0‚1‚…‚n) 为指向子树根结点的指针
简单来说:因为其设计定义为M阶,所以其每一颗枝干最多存储M个关键字,进而其枝干下的子树也就有最大值M,而为了避免根节点的无用,其根节点必定至少要有2个子树,同时为了提高存储效率,与增删查改(下面会讲到)其内部节点至少有[m/2] 个子树,在此为了利于查询其上一阶段点的指针指向的子树需满足大于等于(大于)指针左边的数小于(小于等于)右边的数。
2.2 B+树有哪些特性?
(1)有 M棵子树的节点中含有M个关键字。
(2)所有的叶子结点中包含了全部关键字的信息且叶子节点本身依关键字的大小而自小到大的顺序链接。
(3)所有非叶子结点可以看成是索引部分结点中仅含有其子树中的最大 (最小) 关键字。
(4)其本身遵循的平衡性可以明显降低树的深度,提高了查询速率.
(5)其各节点的有序排列,有利于数据的遍历。
2.3 B+的增删改查。
2.3.1 B+树的查询方法
在B+树的每个非叶子节点中,储存着指针和关键字,并且在每个关键字的前面都有一个指针,关键字左边的指针是指向比关键字小的数据,同理,右边是指向比关键字大的数据。所以在查找某个关键字的时候,先在根节点中找到比该关键字大的最小关键字,然后沿着左边的指针进入第二层节点,在第二层进入相应的节点之后,依然按照上述的方法,在进入第三层节点,直到执行到叶子节点,在叶子节点中找到所要找的数据,如果在内部节点中找到了该数据并不会终止,直到叶子节点才会终子。
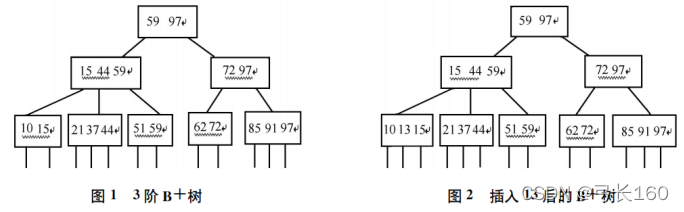
2.3.2 B+树的插入
B+数的插入分为简单插入和复杂插入。不管是哪种插入,都要保证节点中的关键字不会溢出,即不能超过该节点容纳的最多关键字,在插入的时候都是从叶子节点插入,先处理叶子节点,然后再处理根节点。
1.简单插入:如果该叶子节点中的关键字并未达到最多关键字,则把所要插入的数据找到对应的叶子节点,插入即可。如图所示:
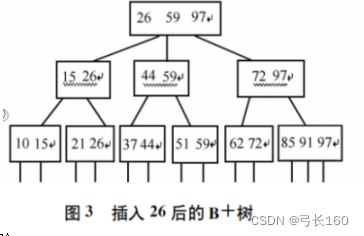
2复杂插入:当所要插入的数据所对应的叶子节点中的关键字达到最多时,及再插入就会 溢出,此时就涉及到叶子节点的分割。即把该叶子节点分割成两个叶子节点,从而保证数据不会溢出。在分割的同时,要遵循平等分割的原理,即保证两个叶子节点的数据较为平衡,这样做的目的是保证了查询效率。当一个叶子节点被分割成两个叶子节点时,被分割后的两个叶子节点中的最大或最小关键字可能会发生改变,我们则需要提取新的最大或最小关键字到根节点中,把所提取到的新的关键字插入到对应的节点中。此时我们应当还要考虑根节点中插入了新的关键字会不会溢出,如果根节点因为插入新的数据也会溢出,则需要用相同的办法,将根节点也分割,再提取根节点中新的关键字到上一个根节点,直到插入关键字之后新的根节点不会再溢出。
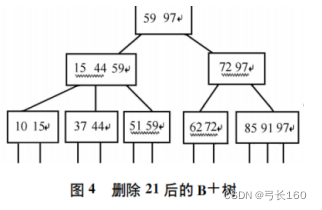
2.3.3 B+树的删除
同B+树的插入一样,B+树的删除也分为简单删除和复杂删除。在删除的同时也要保证叶子节点中的关键字数量不会小于最多关键字的一半。
- 简单删除:如果该叶子节点中的关键字被删除之后,剩余的关键字不少于最多关键字的一半,则可直接删除。同时需要注意的是,所删除的关键字是否为该叶子节点中最大或最小关键字,如果是的话,则所对应的根节点中则要改写新的最大或最小关键字。
- 2.复杂删除:如果该叶子节点中删除关键字之后,剩余的关键字小于一半儿,则需要考虑叶子节点之间的结合。如果该叶子节点左右两边的叶子节点数据未满,如果合并了该叶子节点之后,数据依然不会溢出,则可将该叶子节点与左右叶子节点进行合并。如果与旁边的叶子节点合并之后,旁边的叶子节点会溢出,则从旁边的叶子节点中取出适当的数据加入该叶子节点中,同时提取合并后的叶子节点中的新的最大或最小关键值取代原来根节点中的关键字。
3.总结
随着数据呈现指数级增长,现有的技术也在不断更新换代,B+树的应用领域也在扩大,引用深度也在不断加深。同时B+树的各种机制也在不断改进。例如:提高 B + 树索引的查找效率和空间利用率,同时其衍生出最新的RB+树在填充时不用考虑稀疏系数,其每个节点都是填充满的,提高了空间利用率,而且减少了内部节点的数量,进而降低了树的深度。
由此可知,某一种方法会落后,某一门技术会落伍,我们最终需要保持严谨的态度去改进,去优化,去创新。
4.参考文献
[1]RB+树-----一种列存储数据的树型索引结构 胡玉乐,孙莉,王梅东华大学计算机科学与技术学院 计算机研究与发展 235-242,2010。
[2]B+树在数据库索引中的应用 王英强,石永生 长江大学学报 (自然科学版2008年3月 第5卷 第1期:理工 Mar∙2008‚Vo∙l 5No∙1:Sci & Eng。
[3]B + 树索引机制的研究及优化 施 恩,顾大权,冯 径,赵章明 计算机应用研究 Vol. 34 No. 6 Jun. 2017。
[4]百度百科。
--------------------如有侵权请及时联系删除。