问题描述
小S正在帮助她的朋友们建立一个搜索引擎。为了让用户能够更快地找到他们感兴趣的帖子,小S决定使用倒排索引。倒排索引的工作原理是:每个单词都会关联一个帖子ID的列表,这些帖子包含该单词,且ID按从小到大的顺序排列。
例如,单词“夏天”可能出现在帖子1、帖子3和帖子7中,那么这个单词的倒排链就是 [1, 3, 7]。如果用户想同时找到包含“夏天”和“海滩”的帖子,小S需要找出两个倒排链的交集,且将结果按照从大到小的顺序输出。现在,给定两个单词的倒排链数组 a 和 b,请你帮助小S找出同时包含这两个单词的帖子ID,并按从大到小的顺序返回结果。
测试样例
样例1:
输入:
a = [1, 2, 3, 7], b = [2, 5, 7]
输出:[7, 2]
样例2:
输入:
a = [1, 4, 8, 10], b = [2, 4, 8, 10]
输出:[10, 8, 4]
样例3:
输入:
a = [3, 5, 9], b = [1, 4, 6]
输出:[]
样例4:
输入:
a = [1, 2, 3], b = [1, 2, 3]
输出:[3, 2, 1]
^_^:这个问题的核心是找出两个排序数组的交集,然后按从大到小的顺序输出结果。为了高效地完成任务,我们可以使用双指针的方法。
思路:
- 交集操作:我们需要找到两个数组
a和b的交集。由于两个数组都是按升序排列的,我们可以使用双指针方法来并行扫描两个数组,找出它们的共同元素。 - 排序结果:题目要求输出交集结果按从大到小的顺序排列。我们可以在得到交集后,直接对结果进行反转。
双指针算法:
- 我们维护两个指针,分别指向数组
a和b的起始位置。 - 如果
a[i] == b[j],则这是一个共同的元素,加入结果中,并同时移动两个指针。 - 如果
a[i] < b[j],说明a[i]在数组a中位置较小,应当增加指针i来找到更大的值。 - 如果
a[i] > b[j],则应该增加指针j来找到更大的值。 - 最后,我们得到的交集结果是按升序排列的,只需要反转它即可得到按降序排列的结果。
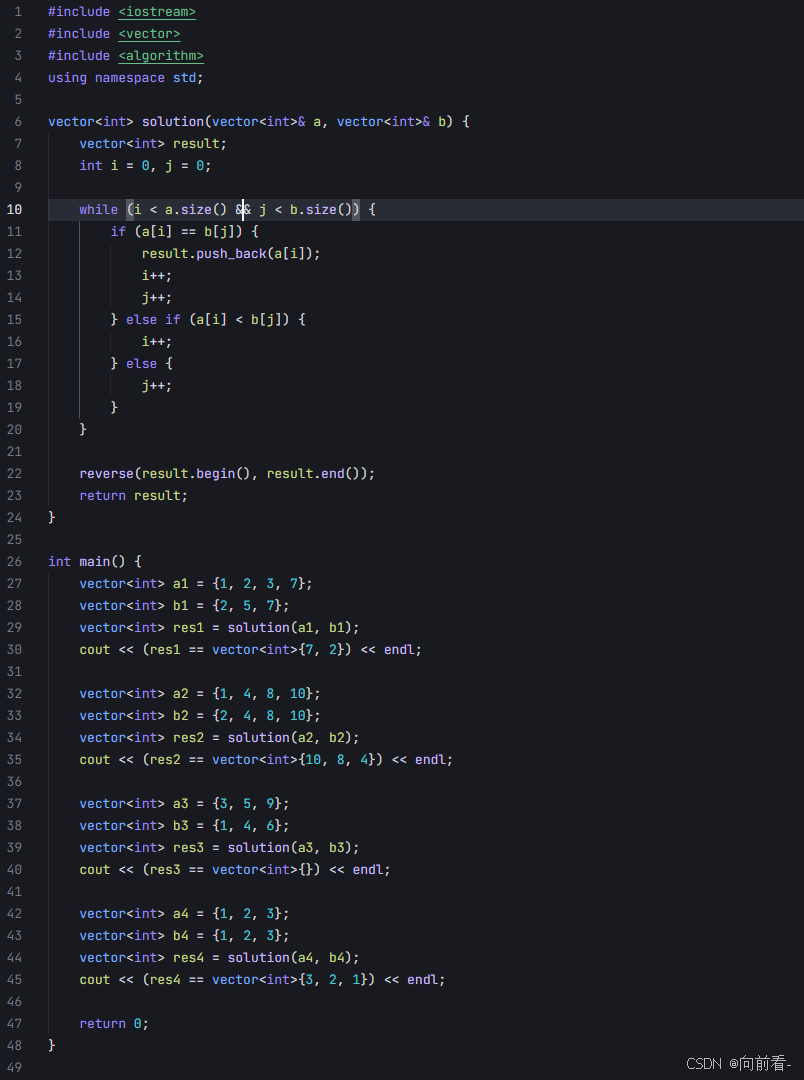
代码:
解释:
-
双指针:我们使用
i和j来遍历两个数组a和b。每次比较a[i]和b[j]的大小,确保两者按升序合并到result中。对于匹配的元素,增加两个指针;否则,增加较小的那个指针。 -
结果反转:最终得到的
result是按升序排列的,因此我们使用reverse(result.begin(), result.end())来反转它,得到按降序排列的交集。 -
边界条件:如果两个数组没有交集,
result会保持为空。最后返回空数组。
测试:
代码中包含了多个测试用例,可以验证该方法的正确性:
- 样例1:
a = [1, 2, 3, 7],b = [2, 5, 7]→ 交集为[2, 7],反转后输出[7, 2]。 - 样例2:
a = [1, 4, 8, 10],b = [2, 4, 8, 10]→ 交集为[4, 8, 10],反转后输出[10, 8, 4]。 - 样例3:
a = [3, 5, 9],b = [1, 4, 6]→ 没有交集,输出[]。 - 样例4:
a = [1, 2, 3],b = [1, 2, 3]→ 交集为[1, 2, 3],反转后输出[3, 2, 1]。
时间复杂度:
- 双指针遍历两个数组,每个数组最多遍历一次,因此时间复杂度是 O(n + m),其中
n和m分别是数组a和b的长度。 - 反转结果数组的时间复杂度是 O(k),其中
k是交集的大小。
空间复杂度:
- 结果数组
result的空间复杂度是 O(k),其中k是交集的大小。