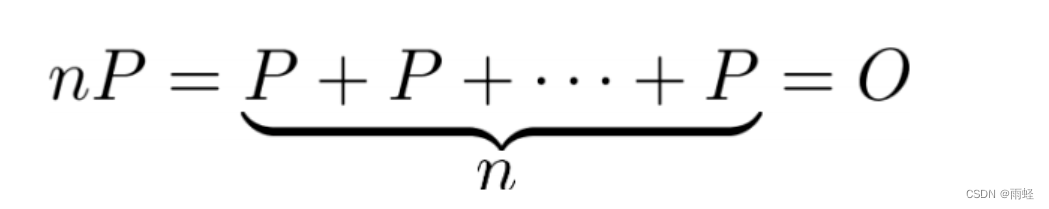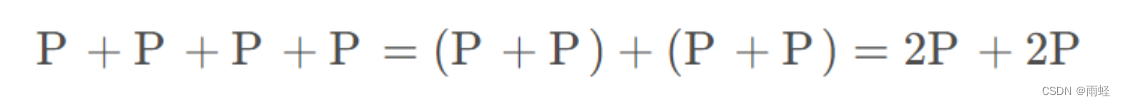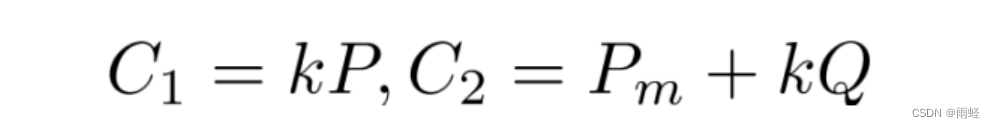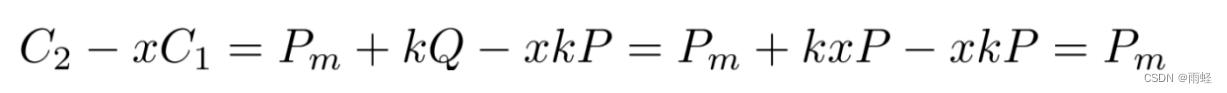一.相关概念

1.点P的阶的概念：

椭圆曲线 $E_p$(a,b)上的点P的阶指的是满足：

的最小正整数n的值，记作ord§，其中O是无穷远点。

2.椭圆曲线上的离散对数问题（elliptic curve discrete logarithm problem:ECDLP)：

设G是椭圆曲线 $E_p$(a,b)上的一个循环子群，P是G的一个生成元，Q $ϵ$ G，已知P和Q，求一个整数m（0<=m<=ord§-1），使得m满足：mP=Q。这个问题称为椭圆曲线上的离散对数问题。

困难点：

当我们计算mP的时候，累加m-1次来计算Q是一种很愚蠢的办法。因为椭圆曲线上的点满足结合律，即( A + B ) + C = A + ( B + C )，扩展一下，就有 ：

比如计算16 P ，我们可以先计算2 P = P + P；然后计算4 P = P + P + P + P = 2 P + 2 P；再计算8 P = P + P . . . + P = 4 P + 4 P ；最后计算16 P = 8 P + 8 P 。这里我们把15次加法减少到了4次。

所以，对于任意的整数m,我们都可以利用这个方法将计算m∗ P所需的加法计算次数降低到约${log}_2$m次。如当m=$2^{2048}$时，我们只需计算2048次，而对手却需要32317006071311007300714876688669951960444102669715484032130345427524655138867890893197201411522913463688717960921898019494119559150490921095088152386448283120630877367300996091750197750389652106796057638384067568276792218642619756161838094338476170470581645852036305042887575891541065808607552399123930385521914333389668342420684974786564569494856176035326322058077805659331026192708460314150258592864177116725943603718461857357598351152301645904403697613233287231227125684710820209725157101726931323469678542580656697935045997268352998638215525166389437335543602135433229604645318478604952148193555853611059596230656次。这无疑是非常困难的。

二.椭圆曲线加密

利用椭圆曲线进行加密时，首先需要将要发送的明文m编码为椭圆曲线上的点$P_m$=（$x_m$,$y_m$），然后再对点$P_m$做加密变换，解密得到$P_m$后还得逆向破译才能获得明文m。

下面是加解密流程：

1.密钥生成：

在椭圆曲线上选取一个阶为n（n是一个大素数）的生成元P，随机选取整数x（1<x<n），计算Q=xP。公钥为Q，私钥为x。

2.加密：

为了加密$P_m$，随机选取一个整数k（1<k<n），计算:

则密文c=($C_1$,$C_2$)。

3.解密：

计算：

4.困难性

攻击者想要从c=($C_1$,$C_2$)计算出$P_m$（主要是从$C_2$推出$P_m$），就必须知道k。而要从P和kP（也就是$C_1$）中能够计算出k是椭圆曲线上的离散对数问题，困难。

而要从P和kP（也就是$C_1$）中能够计算出k是椭圆曲线上的离散对数问题，困难。