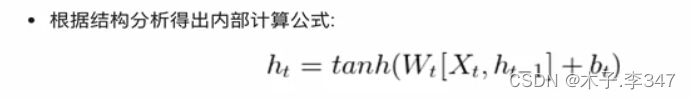RNN（循环神经网络）

在这里插入图片描述

1.RNN简介

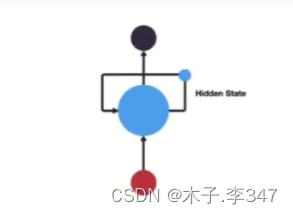
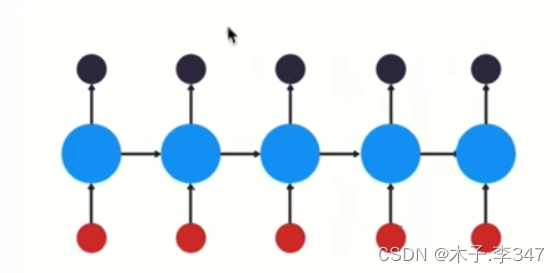
RNN(Recurrent Neural Network), 中文称作循环神经网络,它一般以序列数据为输入，通过网络内部的结构设计有效捕捉序列之间的关系特征,一般也是以序列形式进行输出.
在这里插入图片描述

RNN的循环机制使模型隐层上一时间步产生的结果,能够作为当下时间步输入的一部分(当下时间步的输入除了正常的输入外还包括上一步的隐层输出)对当下时间步的输出产生影响.

结构：三层，输入、输出、隐藏层（循环在隐藏层）

1.1RNN模型的作用:

因为RNN结构能够很好利用序列之间的关系,因此针对自然界具有连续性的输入序列,如人类的语言,语音等进行很好的处理,广泛应用于NLP领域（自然语言处理）的各项任务,如文本分类,情感分析,意图识别,机器翻译等.

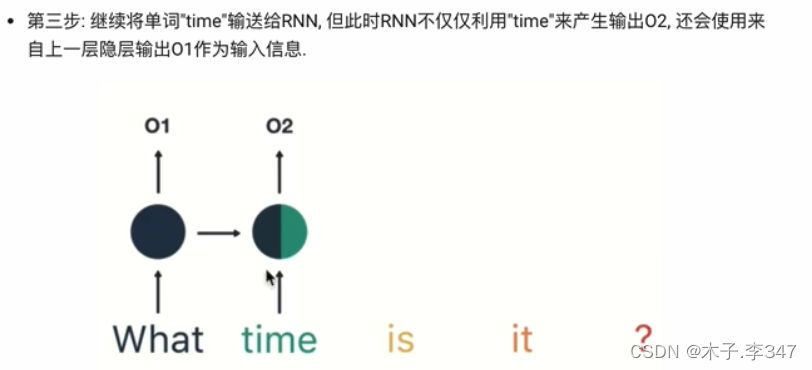
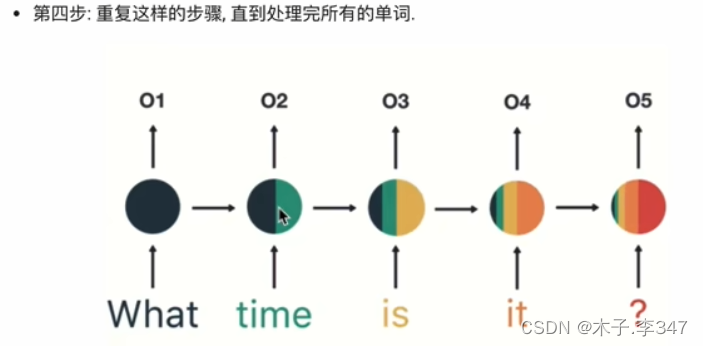
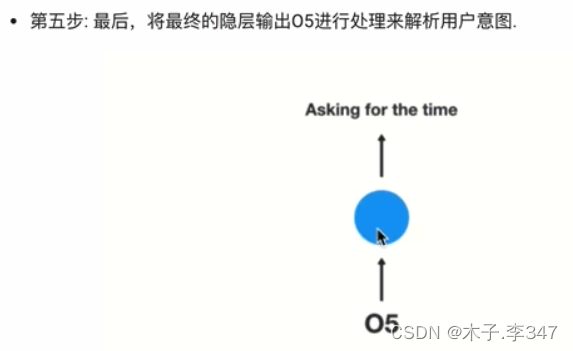
语言处理示例

1.2RNN的分类

1.2.1按照输入、输出的结构分类

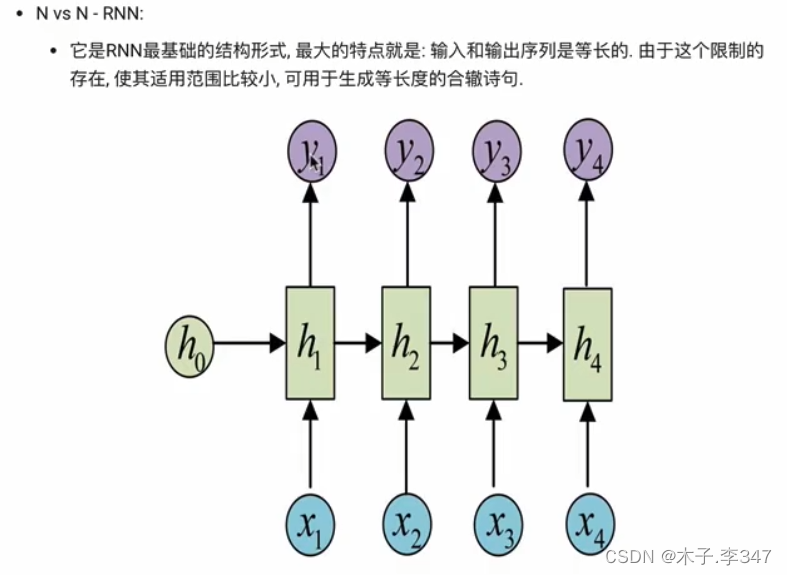
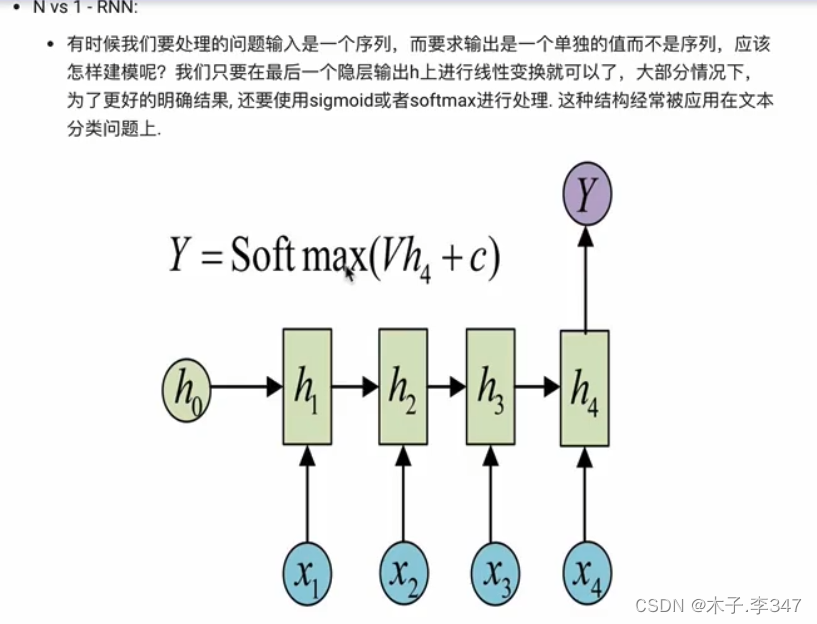
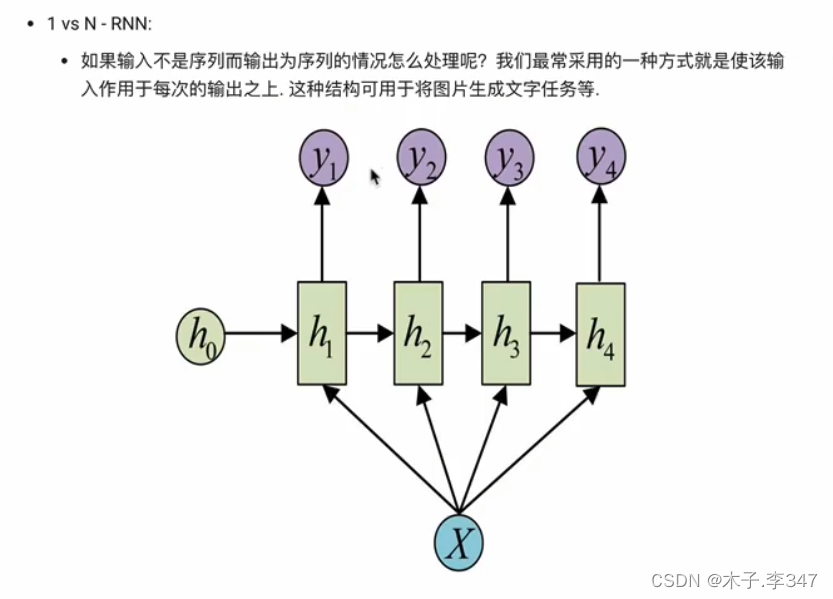
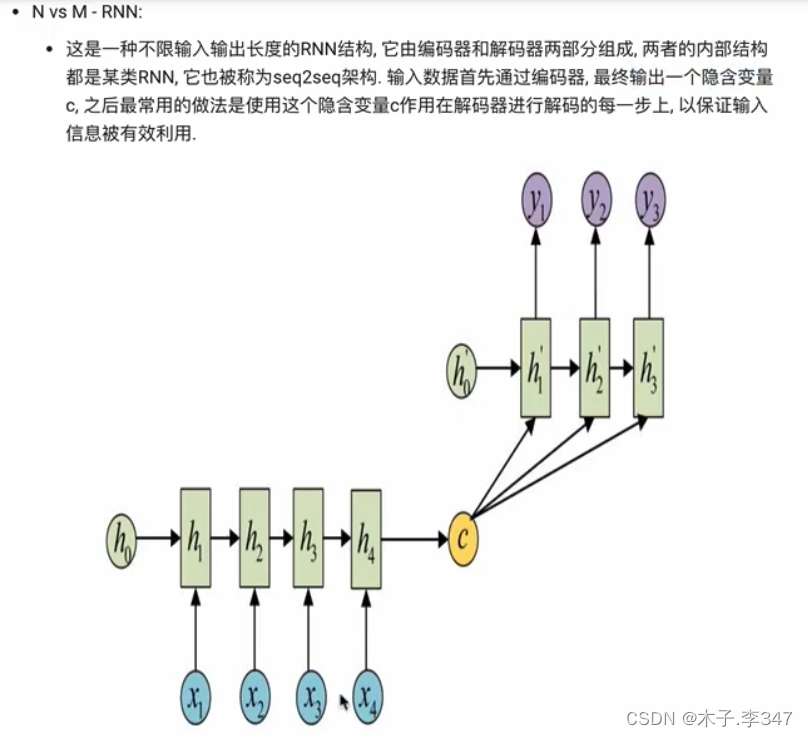
N vs M：即N个输入，M个输出的RNN

在这里插入图片描述

相当于编码器（左下：N对1）和解码器（右上：1对M）

在这里插入图片描述

1.2.2按照RNN内部构造分类

RNN本身缺点：不可并行计算，故当数据量和模型体量过大会制约其发展；transform可改善其不可并行计算的问题。

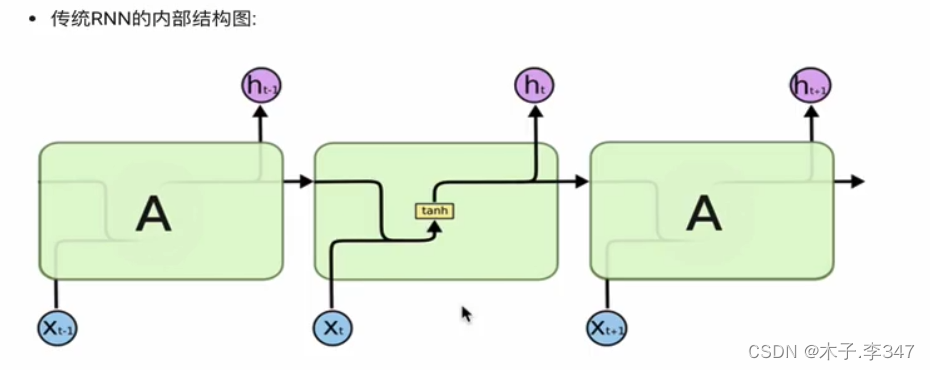
在这里插入图片描述

2.传统RNN

在这里插入图片描述

图中,括号内的为全连接层（线性层）
激活函数（tanh）：用于帮助调节流经网络的值, tanh函数将值压缩在-1和1之间.

2.1 Pytorch中传统RNN工具的使用

位置:在torch.nn工具包之中,通过torch.nn.RNN可调用.

在这里插入图片描述

torch.nn.RNN详解

import torch
import torch.nn as nn

rnn=nn.RNN(5,6,2)#实例化rnn对象
#参数1：输入张量x的维度-input_size
#参数2：隐藏层的维度（隐藏层神经元个数）-hidden_size
#参数3：隐藏层的层数-num_layers

#torch.randn-随机产生正态分布的随机数
input1=torch.randn(1,3,5)#设定输入张量x-1层3行5列
#参数1：输入序列长度-sequence_lengh
#参数2：批次的样本-batch_size（表示：3个样本每个样本一个字母（序列长））
#参数3：输入张量x的维度-input_size

h0=torch.randn(2,3,6)#设定初始化的h0
#第一个参数: num_layers * num_directions(层数+网络方向数(1或2))
#第二个参酸: batch_size(批次的样本数)
#第三个参酸: hidden_size(隐藏层的维度)

output,hn=rnn(input1,h0)
#最后输出和最后一层的隐藏层输出

print(output)
print(output.shape)
print(hn)
print(hn.shape)

在这里插入图片描述

摘录自-循环神经网络 - RNN基本原理详解

2.2传统RNN优缺点

优势：
由于内部结构简单,对计算资源要求低,相比之后我们要学习的RNN变体:LSTM和GRU模型参数总量少了很多,在短序列任务上性能和效果都表现优异.
缺点:
传统RNN在解决长序列之间的关联时,通过实践，证明经典RNN表现很差,原因是在进行反向传播的时候,过长的序列导致梯度的计算异常,发生梯度消失或爆炸.
NaN值：(Not a Number,非数)是计算机科学中数值数据类型的一类值,表示未定义或不可表示的值。

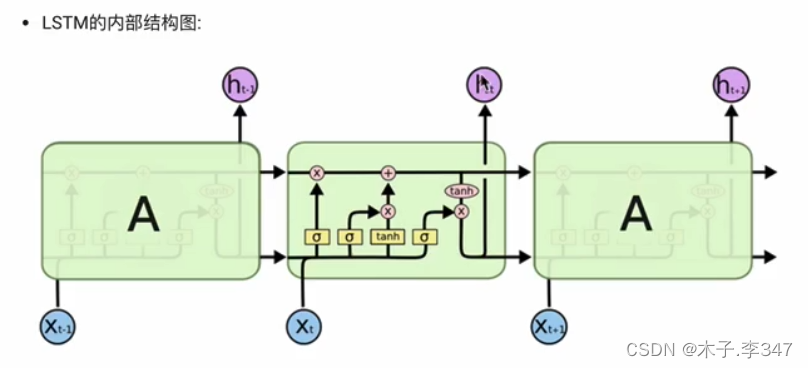
3.LSTM模型

3.1 LSTM简介

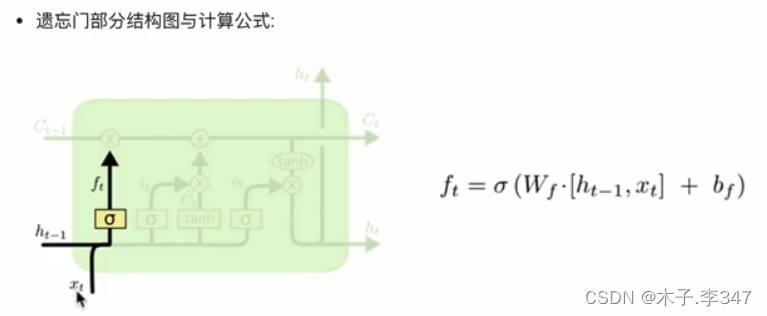
在这里插入图片描述

3.1.1 遗忘门

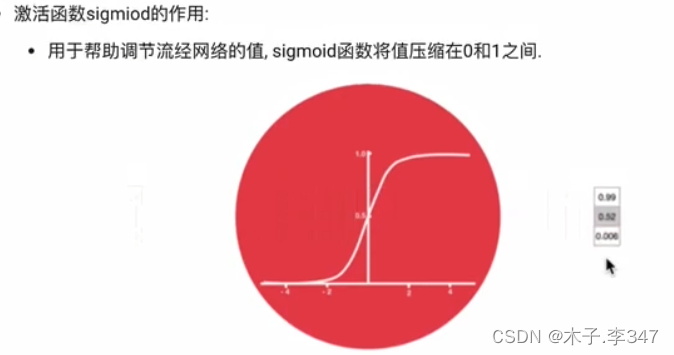
在这里插入图片描述

图中sigma为sigmiod函数，将值压缩在0-1之间。

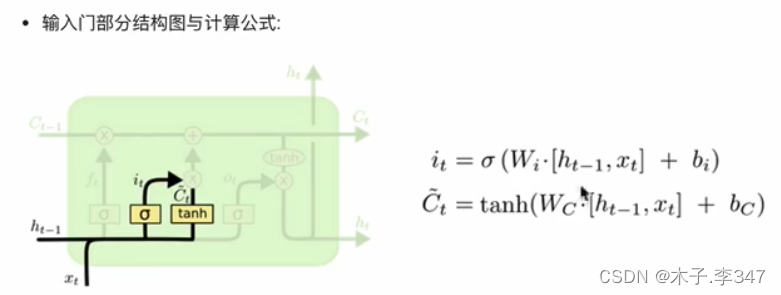
在这里插入图片描述

3.1.2 输入门

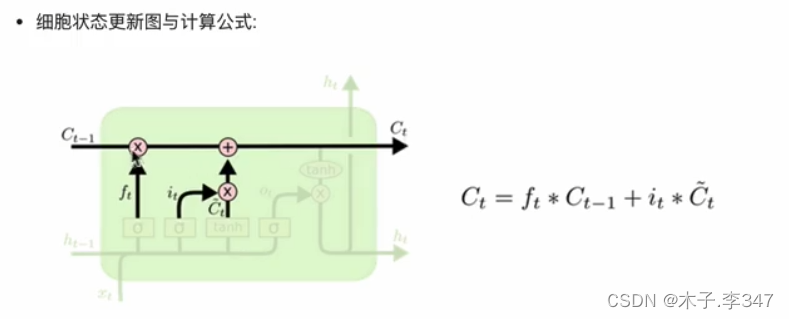
在这里插入图片描述

3.1.3 细胞状态

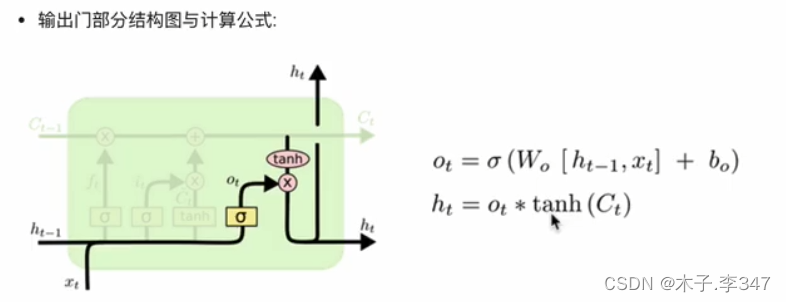
在这里插入图片描述

3.1.4 输出门

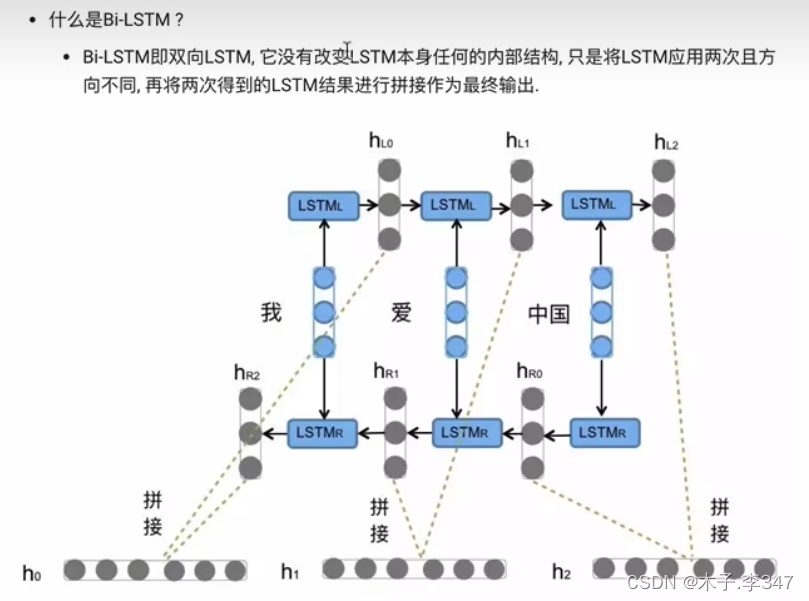
在这里插入图片描述

3.2Bi-LSTM

在这里插入图片描述

3.3 Pytorch中LSTM工具的使用

在这里插入图片描述

import torch
import torch.nn as nn

lstm=nn.LSTM(5,6,2)#实例化rnn对象
#参数1：输入张量x的维度-input_size
#参数2：隐藏层的维度（隐藏层神经元个数）-hidden_size
#参数3：隐藏层的层数-num_layers

input1=torch.randn(1,3,5)#设定输入张量x-1层3行5列
#参数1：输入序列长度-sequence_lengh
#参数2：批次的样本-batch_size（表示：3个样本每个样本一个字母（序列长））
#参数3：输入张量x的维度-input_size

h0=torch.randn(2,3,6)#设定初始化的h0（隐藏层）
c0=torch.randn(2,3,6)#设定初始化的c0（细胞状态）
#第一个参数: num_layers * num_directions(层数+网络方向数(1或2))
#第二个参酸: batch_size(批次的样本数)
#第三个参酸: hidden_size(隐藏层的维度)

output,(hn,cn)=lstm(input1,(h0,c0))
#最后输出和最后一层的隐藏层输出

print(output)
print(output.shape)
print(hn)
print(hn.shape)
print(cn)
print(cn.shape)

在这里插入图片描述

3.4 LSTM优缺点

在这里插入图片描述

4.GRU模型

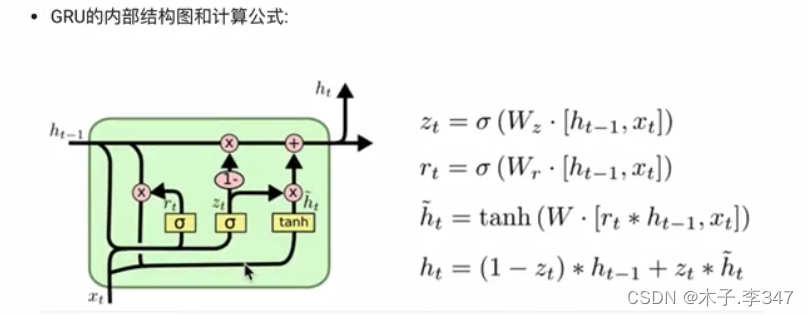
4.1GRU简介

在这里插入图片描述

4.2Pytorch中LSTM工具的使用

import torch
import torch.nn as nn

gru=nn.GRU(5,6,2)#实例化rnn对象
#参数1：输入张量x的维度-input_size
#参数2：隐藏层的维度（隐藏层神经元个数）-hidden_size
#参数3：隐藏层的层数-num_layers

input1=torch.randn(1,3,5)#设定输入张量x-1层3行5列
#参数1：输入序列长度-sequence_lengh
#参数2：批次的样本-batch_size（表示：3个样本每个样本一个字母（序列长））
#参数3：输入张量x的维度-input_size

h0=torch.randn(2,3,6)#设定初始化的h0
#第一个参数: num_layers * num_directions(层数+网络方向数(1或2))
#第二个参酸: batch_size(批次的样本数)
#第三个参酸: hidden_size(隐藏层的维度)

output,hn=gru(input1,h0)
#最后输出和最后一层的隐藏层输出

print (output)
print(output.shape)
print(hn)
print(hn.shape)

在这里插入图片描述

4.3GRU优缺点

在这里插入图片描述

5.注意力机制

5.1简介

5.1.1注意力

在这里插入图片描述

Q：查询向量
K：键向量
V：值向量
常规注意力机制;Q!=K=V；自注意力机制：Q=K=V

在这里插入图片描述

softmax：归一化指数函数

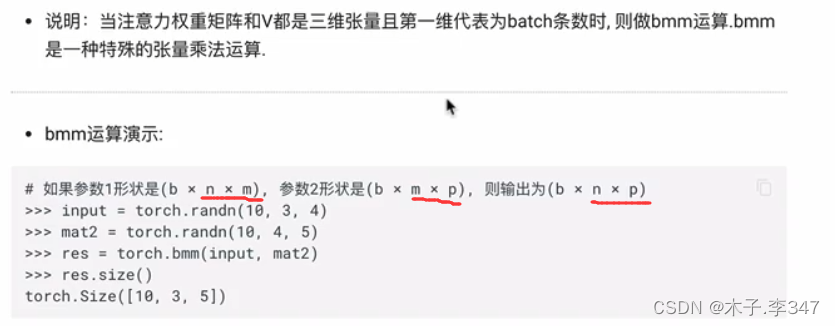
在这里插入图片描述

5.1.2注意力机制

在这里插入图片描述

bmm运算：可实现与应用网络融为一体

在这里插入图片描述

5.1.3 代码实现

在这里插入图片描述

按照上述步骤进行实现：

import torch
import torch.nn as nn
import torch.nn.functional as F

class Attn(nn.Module):
    def __init__(self,query_size,key_size,value_size1,value_size2,output_size):
        # query_size表示Q的最后一个维度大小，key_size表示K的最后一个维度大小
        #value_size1表示V的倒数第二维大小；value_size2表示V的倒数第一维（最后一维）大小
        # V的尺寸表示(1,value_size1,value_size2)
        # output_size表示输出的最后一个维度的大小

        super(Attn, self).__init__()#单继承，即只有一个父类（nn.Module）
        # 对继承自(Attn的父类)父类nn.Module的属性进行初始化。而且是用nn.Module的初始化方法来初始化继承的属性。
        self.query_size=query_size
        self.key_size = key_size
        self.value_size1=value_size1
        self.value_size2=value_size2
        self.output_size=output_size

        # 初始化注意力机制实现中第一步的线性层
        self.attn=nn.Linear(self.query_size+self.key_size,self.value_size1)
        #Linear（x,y）中下x、y分别表示输入和输出的值（包括大小也要一致）

        # 初始化注意力机制实现中第三步的线性层
        self.attn_combine = nn.Linear(self.query_size + self.value_size2, self.output_size)

    def forward(self,Q,K,V):
        #注意：假定Q、K、V都是三维张量
        #按照第一种注意力计算规则进行计算：Softmax(Linear([Q,K])).V
        #第一步，将Q、K进行纵轴的拼接，然后做一次线性变换，最后使用softmax进行处理得到注意力向量
        attn_weights=F.softmax(self.attn(torch.cat((Q[0],K[0]),1)),1)
        #torch.cat((Q[0],K[0]),1))表示：将两者（Q[0]和K[0]）在第一维度上进行拼接
        #self.attn(torch.cat((Q[0],K[0]),1))中将torch.cat((Q[0],K[0])作为线性层的输入
        
        #将注意力矩阵和V进行一次bmm运算（即将权重矩阵与V进行乘法运算）
        #因为二者都是三维张向量且第一维代表batch条数，故而做bmm运算
        attn_applied=torch.bmm(attn_weights.unsqueeze(0),V)
        #attn_weights.unsqueeze(0)表示：将attn_weights扩充维度（在第0层）；原本为1*32->1*1*32

        #第二步，根据第一步采用的计算方法（拼接或转置点积），
        # 此处第一步用拼接方法，需要将Q与上一步计算结果拼接
        #取Q[0]进行降维，与上面得运算结果进行一次拼接
        output=torch.cat((Q[0],attn_applied[0]),1)

        #第三步：将上面的输出进行一次线性变换，然后在扩展成三维张量
        output=self.attn_combine(output).unsqueeze(0)
        return output,attn_weights

#调用实现：
query_size=32
key_size=32
value_size1=32
value_size2=64
output_size=64

attn=Attn(query_size,key_size,value_size1,value_size2,output_size)
Q=torch.randn(1,1,32)
K=torch.randn(1,1,32)
V=torch.randn(1,32,64)
output=attn(Q,K,V)

print(output[0])
print(output[0].size())
print(output[1])  #注意力权重
print(output[1].size())

在这里插入图片描述
对forward函数进行考察：

 print('catshape==',torch.cat((Q[0],K[0]),1).shape)
 print('attnshape==',self.attn(torch.cat((Q[0],K[0]),1)).shape)
 print('attn_weights==',attn_weights.shape)#权重矩阵

 print('attn_applied==',attn_applied.shape)
 print('outputshape==',output.shape)
 print(output[0].size())
 print(output[1].size())

在这里插入图片描述

分析：
Q、K的第0层（都是1* 32）进行纵轴拼接，输出1* 64；
拼接后的结果经线性层后（此处线性层输入要求32+32=64，正好符合）输出1* 32；
再经softmax后还是1* 32；
权重矩阵经扩维后变为1* 1* 32，与V（1* 32* 64）进行bmm计算，输出1* 1* 64；
之后其第0层（1* 64）与Q0进行纵轴拼接，输出1* 96；
再经线性层输出out_size尺寸，即1* 64，再扩维成1* 1* 64

注：参考资料