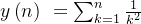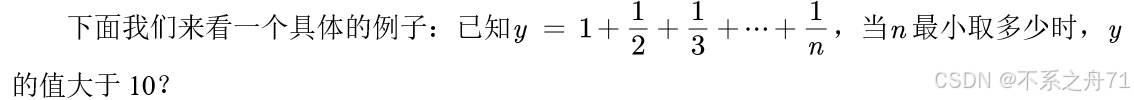matlab学习笔记：第四章4.2循环语句

1.for-end语句

1.1for-end语句(简称for循环)

用于事先已知循环次数的情形：

在该语法中，循环变量是用于迭代的变量名，它会在每次循环迭代中从向量或矩阵中取出一列的值。数值向量或者矩阵则表示了循环变量可以取值的范围，通常根据实际需要事先给定。一旦循环变量遍历完数值向量或者矩阵中的所有值，循环就会结束。

1.2例题

（1）不使用sum函数，计算行向量x中所有元素的和。

s = 0;
x = [5 8 9 1 4 3 7];
for i = x
    s = s + i;
end
disp(s)

（2）如果x是一个列向量，左侧的代码输出的s是什么，应该如何修改代码？

s = 0;
x = [3;5;9;8];
for i = transpose(x)
    s = s + i;
end
disp(s)

（3）计算当n等于100时，下面式子的结果:

$y\left( n \right) \,\,=\,\,1+\frac{1}{2^2}+\frac{1}{3^2}+\cdots +\frac{1}{n^2}$

写成求和形式： $y\left( n \right) \,\,=\sum_{k=1}^n{\frac{1}{k^2}}$

x = 1:100;
k = 0;
x1 = 1 ./ (x .^2);
for i = x1
    k = k + i;
end
disp(k)

（4）计算当n从1一直取到100时，上一小问式子 $y\left( n \right) \,\,=\,\,1+\frac{1}{2^2}+\frac{1}{3^2}+\cdots +\frac{1}{n^2}$ 的计算结果，

并将计算结果保存到一个长度为100的行向量S中。

S = zeros(1,100);
for n = 1:100
    y = 0;
    for k = 1:n
        y = y + 1 / (k^2);
    end
    S(n) = y;
end
disp(S)
%优化后，不嵌套循环
S = [];
y = 0;
for k = 1:100;
    y = y + 1 / (k^2);
    S = [S,y]
end
disp(S)

（5）计算从公元1年到公元9999年间，有多少个闰年。闰年的判读条件是年份能够被4整除，但不能被100整除，或者年份能够被400整除。

R = [];
for n = 1:9999
    if (mod(n,4) == 0)  & (mod(n,100) ~= 0)
        R = [R,n];
    elseif mod(n,400) == 0
        R = [R,n];
    end
end
num = sum(logical(R))   %闰年的数量，闰年的年份储存在了S向量中。

（6）一个三位正整数各位数字的立方和等于该数本身则称该数为水仙花数，例如：1^3 + 5^3+ 3^3 = 153，则153是水仙花数。请你找出所有的水仙花数并将其保存到向量S中。

S = [];
for n = 100:999
    N = num2str(n);
    N1 = str2num(N(1));
    N2 = str2num(N(2));
    N3 = str2num(N(3));
    if N1^3 + N2^3 + N3^3 == n
        S = [S,n];
    end
end
disp(S)

（7）斐波那契数列的递推公式为 $\left\{ \begin{array}{l} F\left( 1 \right) =1,F\left( 2 \right) =1\\ F\left( n \right) =F\left( n-1 \right) +F\left( n-2 \right) , n\,\,\ge 3\\ \end{array} \right.$ ，求F（30）。

F = ones(1,30);
for n = 3:30
    F(n) = F(n-1) + F(n-2);
end
disp(F(30))

（8）生成一个5行8列的矩阵，矩阵中每个元素都是在区间[1, 10]上取值的随机整数。接下来请循环每一列，若发现同一列的五个元素各不相同，则保留该列；若该列中有重复的元素则删除该列。

A = randi([1,10],5,8);
B = [];
for a = A
    a1 = diff(sort(a));
    if sum(logical(find(~a1))) == 0
        B = [B,a];
        end
end
B

1.3注意事项：

(1)若for语句后面的向量或者矩阵为空，则循环一次也不会被执行。

(2)for语句后面的向量或者矩阵只会在循环开始时使用一次，向量或者矩阵元素一旦确定将不会再改变。即使你在循环体中改变向量或者矩阵的值，循环变量的值也不改变。

(3)可以在循环体中修改循环变量的值，但当程序执行流程再次回到循环开始时，循环变量会自动恢复成向量或者矩阵的下一列元素。

2.while-end语句

2.1while语句

除了for-end语句之外，MATLAB还提供了另一种强大的循环语句：while-end语句（简称while循环）。与for循环不同，while循环的特点在于它允许我们在不知道具体循环次数的情况下执行循环体，这种灵活性使得while循环在某些情境下非常有用，尤其是当我们需要满足某些某些条件时才执行循环操作。

y = 1;
n = 1;
while y <= 10
    n = n + 1;
    y = y + 1/n;
end
disp(n)

a(1) = 1;
a(2) = 1;
n = 2;
while a(n) <= 9999;
    n = n + 1;
    a(n) = a(n-1) + a(n-2);
end
disp(a(end))

y = 1;  
n = 1;
while n < 100
    n = n + 1;
    y = y + 1/n; 
end
disp(y)

2.2注意事项：

（1）如果不小心执行了一个无限循环（即永远不会自行结束的循环，又称死循环），

可以按下 Ctrl+C 停止执行程序。

（2）while后面表达式的计算结果不一定非得是逻辑值1或0。如果表达式的计算结果是一个数值常数，则只有当这个常数为非零值时循环才会进行；若表达式的计算结果是一个数值向量或者矩阵，则仅当该向量或矩阵中的所有元素都是非零数时循环才会进行。

3.break和continue

3.1关键词介绍

break关键字用于终止执行 for 或 while 循环。
continue关键字用于跳过循环的当前迭代，然后继续下一次迭代。

n = 1e8;
S = 0;
for k = 1:n
    S = S + 1/k;
    if S > 10
        disp(k)
        break
    end
end

（2）使用循环输出1至10中所有的奇数。

for i = 1:10
    if mod(i,2) == 0
        continue
    else
        disp(i)
    end
end

注意，如果存在循环的嵌套，break和continue 仅在调用它的循环的主体中起作用。即break 仅从它所发生的循环中退出，continue 仅跳过它所发生的循环体内的剩余语句。

3.2例题

（1）判断质数问题

n = 135389;  % 输入要判断的数n
is_prime = true;   % 初始化标志变量is_prime为true，此时代表n是质数
for ii = 2:n-1  % 思考：如何缩小循环遍历的范围来提高代码运行的效率，留作本章课后习题
    % 检查ii是否能够整除n
    if mod(n, ii) == 0
        % 如果能整除，则n不是质数，将标志变量is_prime重新赋值为false
        is_prime = false;
        break;  % 跳出循环
    end
end

（2）扑克牌炸弹问题

A = [1:13];
poke = [repmat(A,1,4),14,15];
k = 1;
while true
    ind = randperm(54,17);
    nmp = sort(poke(ind));
    v1 = all(ismember([14,15],nmp));
    v2 = false;
    for i = 1:13
        if sum(nmp == i) == 4
            v2 = true;
            break
        end
    end
    if (v1 | v2) == 1
        break
    else
        k = k + 1;
    end
end
disp(k)

（3）一只失明的小猫掉进山洞里，山洞有三个门，其中进入第一个门后走2h后可以回到地面，进入第二个门后走4h会回到原始的出发点，进入第三个门后走6h还是回到原始的出发点。假设小猫每次都随机地选择这三个门中的一个进入，求小猫走出山洞的期望时间？

n = 10000       % 设置模拟的次数
T = zeros(1,n); % T用来存储每次模拟得到的时间
for k = 1:n     % 开始进行 n 次模拟
    t = 0       % 初始化时间
    while true  % 开始模拟小猫走出山洞的过程
         m = randi([1,3]);  %随机选择第几个门
        if m == 1           % 选择第1个门
            t = t + 2;      % 走2小时回到地面
            break           % 小猫成功走出山洞，结束模拟
        elseif m == 2       % 选择第2个门
            t = t + 4;      % 走4小时回到原始出发点
        elseif m == 3       % 选择第3个门
            t = t + 6;      % 走6小时回到原始出发点
        end
    end
    T(k) = t;               % 记录每次模拟得到的时间
end
E = mean(T)                 % 计算所有模拟结果的平均值，即小猫走出山洞的期望时间的估计

（4）二分搜索法求函数零点

$f(x)=x^3-8x^2+x-5$ f(x)在区间[6,10]递增且f(6)< 0 ,f(10)>0，请用二分搜索法求零点x0（f(x0)和0的误差控制在1e-8内即可）。

a = 6;
b = 10;
vol = 1e-8;
while true
    c = (a + b) / 2;
    fc = c^3-8*c^2+c-5;
    if abs(fc) <= vol
        x0 = c
        break
    end
    if (a^3-8*a^2+a-5) * fc < 0;
        b = c;
    elseif (b^3-8*b^2+b-5) * fc < 0;
        a = c;
    end
end

参考：数学建模清风老师《MATLAB教程新手入门篇》https://www.bilibili.com/video/BV1dN4y1Q7Kt/