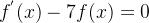一、什么是常微分方程(ODE)
微分方程是包含未知函数及其导数的方程,未知函数导数的最高阶数称为该微分方程的阶
常微分方程(ordinary differential equation,简称ODE)是未知函数只含有一个自变量的微分方程
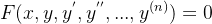
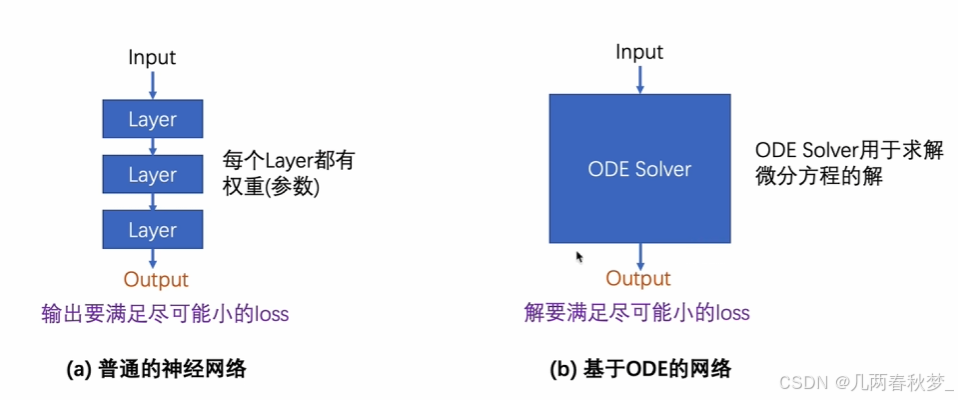
二、Neural ODE与普通神经网络的区别
三、用ODE表示有什么优势
1.Powerful representation:微分方程可以用数值法求解,因此对于任何连续函数都有良好的逼近能力。
2.Memory efficiency:不需要用到反向传播,因此训练上节约内存
3.Simplicity:不需要考虑复杂的调参和网络设计,形式简洁
4.Abstraction:让网络不需要考虑每层需要做什么,只需要考虑怎么计算结果
四、求解微分方程
Neural ODE解的是带初始值的常微分方程
如果给定初识条件(0,1),则
这种解法微分方程满足一定的形式,但实际生活当中原函数比较复杂,通常会使用数值法求解原函数在各个点的值
比较出名的两个方法:① 欧拉法(Euler Method) ② 龙格库塔法 (Runge-Kutta)
欧拉法:
在给定初始条件和f的情况下,利用欧拉法可以推导出任意时刻的函数值