• 当我们在设计达到射频或者毫米波这些高频段的器件仿真的时候，往往对晶体管的性能参数有较高的要求。
• 在这里通过一篇JSSC的论文，我学习到了一个得到晶体管最大性能参数的仿真方法——Gmax
  
• 在仿真设计中，存在很多种类型的功率增益：
  • maximum available gain最大可用增益Gma（相当于cadence的sp仿真的Gmax）
  • maximum stable gain最大稳定增益Gms（相当于cadence的sp仿真的）
  • maximum unilateral gain最大单向增益U
  • maximum achievable gain最大可实现增益Gmax。
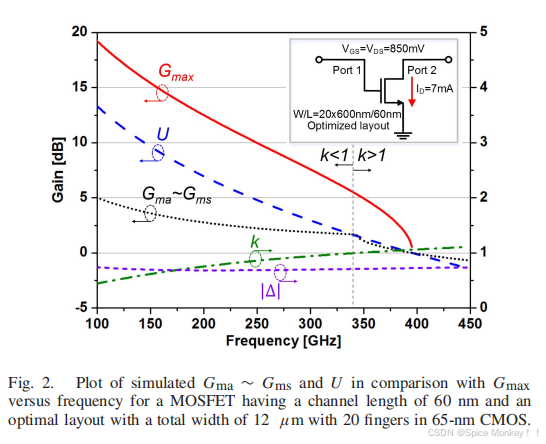
• Fig. 2显示了一个模拟的MOSFET在65纳米CMOS工艺中，拥有60纳米沟道长度和12微米总宽度（共20个指）的功率增益与频率的关系图。可以发现Gmax意味着当使用线性、无损和互惠嵌入网络时，晶体管达到最佳条件下的Gma的最高可能值。
  • k等于1的频率（约340 GHz）将图分成两个区域，即一个可能不稳定区域（k < 1）和一个绝对稳定区域（k > 1）。
  • U、Gma ∼ Gms和Gmax都相交在相同的单位增益（0分贝）频率下，结果是fmax为395 GHz。
  • 在不稳定区域（k<1），U通常高于Gma ∼ Gms，而在接近和处于稳定区域时，这并不总是成立。因此，单边化晶体管对于在高工作频率下的高增益放大器设计并不是一个合适的选择。
  • 最后，最重要的一点是，Gmax可以产生比U和Gma ∼ Gms更高的功率增益。特别是，由于Gma ∼ Gms和U较低以及被动元件的高损耗，在高工作频率范围内采用Gma ∼ Gms和U设计高增益放大器非常困难。因此，在高工作频率的放大器设计中采用Gmax对于高效放大是有利的。
    

Gmax的公式推导

• U可以被表达为一种形式，其中k是稳定性因子
  $$U=\frac{|(S_{21}/S_{12})-1{|}^2}{2k|S_{21}/S_{12}|-2\mathrm{Re}(S_{21}/S_{12})}$$
• Gmax的最终表达式如下（省去了很多中间过程）
  $$G_{\max (\max )}=G_{\max }=(2U-1)+2\sqrt{U(U-1)}$$
• Gmax仅是U的函数。此外，U仅是偏置条件和晶体管的内在属性（如晶体管布局、寄生参数等）的函数。因此，可以从某个晶体管的U值获得Gmax的理论值。

Gmax的性质

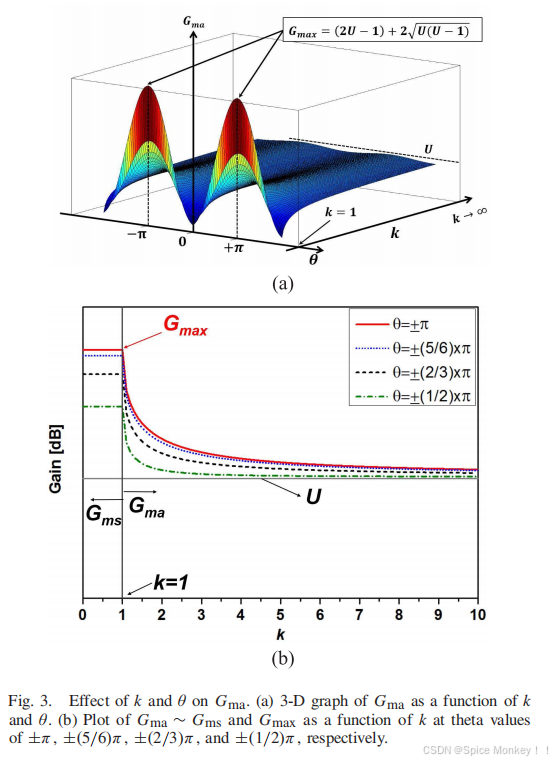
• Figure3显示了Gma关于k和θ的值，可以发现下面一些性质
• 实现Gmax的两个条件
  • 稳定因子k=1
  • 相位差θ=±π
    
    Cadence仿真
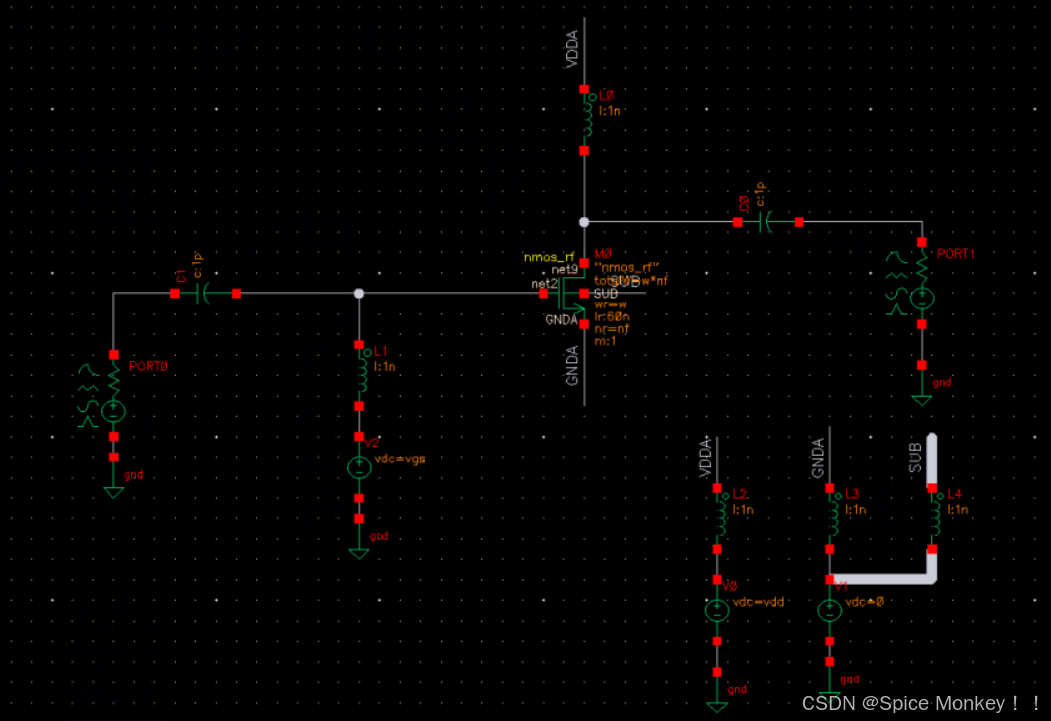
• 这里采用tsmcN65工艺库的nmos_rf晶体管来进行仿真。仿真的电路图如下所示
  
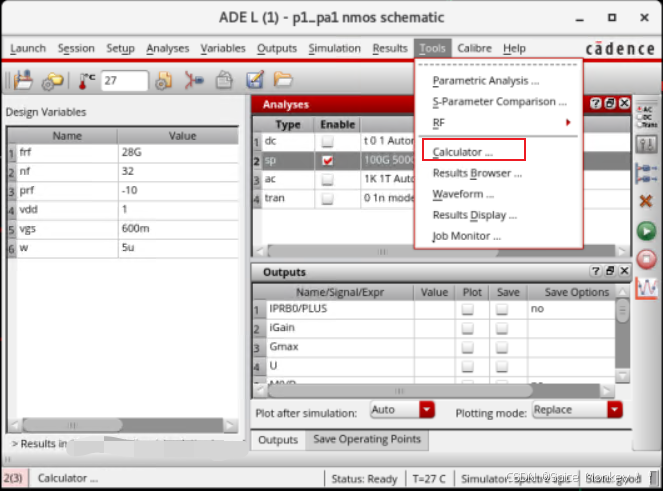
• 打开ADE仿真窗口，首先进行sp仿真，扫描频率为1G-500GHz
• 然后从Tools->Calculators打开计算器，
  
• 复制下面U和Gmax的表达式到Calculator窗口中
• U(YP_dB10)

db10(((abs((ypm('sp 2 1) - ypm('sp 1 2))) * abs((ypm('sp 2 1) - ypm('sp 1 2)))) / (4 * ((real(ypm('sp 1 1)) * real(ypm('sp 2 2))) - (real(ypm('sp 1 2)) * real(ypm('sp 2 1)))))))

• GMAX(YP_dB10)

db10((((2 * ((abs((ypm('sp 2 1) - ypm('sp 1 2))) * abs((ypm('sp 2 1) - ypm('sp 1 2)))) / (4 * ((real(ypm('sp 1 1)) * real(ypm('sp 2 2))) - (real(ypm('sp 1 2)) * real(ypm('sp 2 1))))))) - 1) + (2 * sqrt((((abs((ypm('sp 2 1) - ypm('sp 1 2))) * abs((ypm('sp 2 1) - ypm('sp 1 2)))) / (4 * ((real(ypm('sp 1 1)) * real(ypm('sp 2 2))) - (real(ypm('sp 1 2)) * real(ypm('sp 2 1)))))) * (((abs((ypm('sp 2 1) - ypm('sp 1 2))) * abs((ypm('sp 2 1) - ypm('sp 1 2)))) / (4 * ((real(ypm('sp 1 1)) * real(ypm('sp 2 2))) - (real(ypm('sp 1 2)) * real(ypm('sp 2 1)))))) - 1))))))

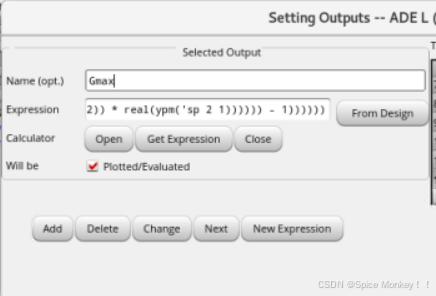
• 点击这个按钮导入到ADE的output窗口中
  
  
• 然后在ADE窗口双击这个表达式，将其命名为Gmax
  
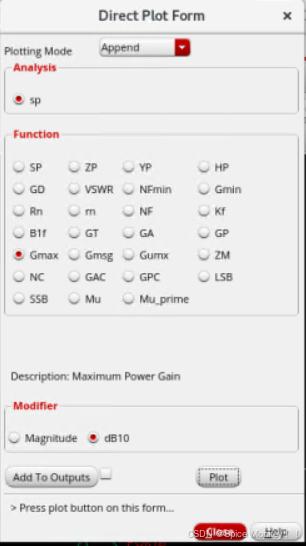
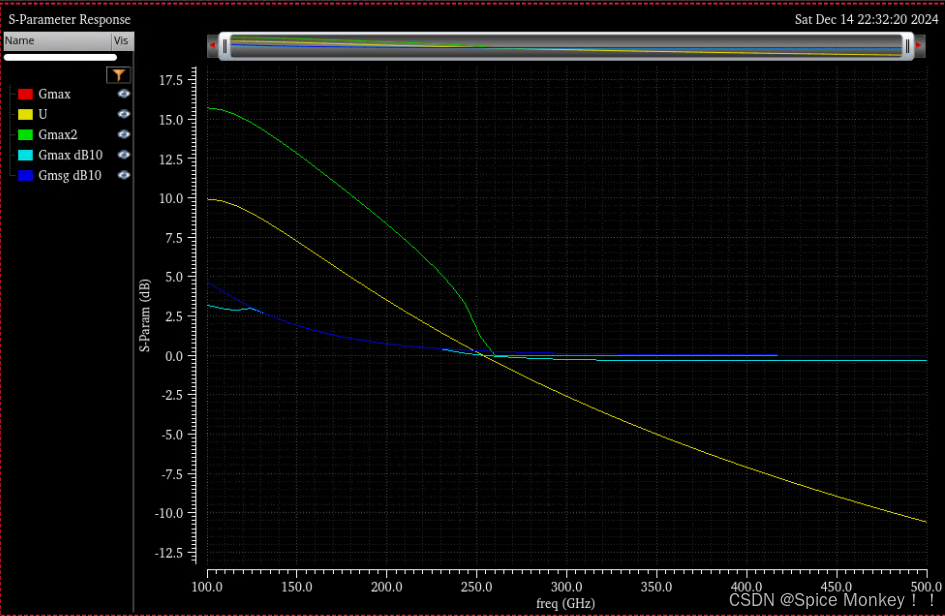
• 上图中的Gmax dB10是sp仿真中的Gmax，对应论文中的Gma
  
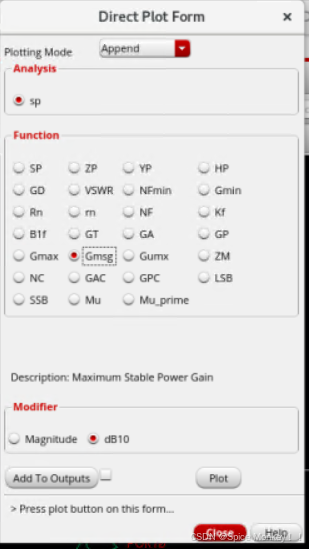
• Gmsg dB10是sp仿真中的Gmsg，对应论文中的Gms
  
• 然后就可以绘制出下图（这里Gmax和Gmax2是一条曲线，重合了）
• 其中Gmax为0dB对应的频率就是fmax