论文结构目录
论文地址:Liu_Learning_to_Upsample_by_Learning_to_Sample_ICCV_2023_paper.pdf
代码地址:https://github.com/tiny-smart/dysample.git
一、之前的上采样器
随着动态网络的普及,一些动态上采样器在几个任务上显示出巨大潜力。CARAFE通过动态卷积生成内容感知上采样核来对特征进行上采样。后续工作FADE和SAPA提出将高分辨率引导特征和低分辨率输入特征结合起来生成动态核,以便上采样过程能够受到更高分辨率结构的引导。这些动态上采样器通常结构复杂,推理时间成本高,特别是对于FADE和SAPA,高分辨率引导特征引入了更多的计算工作量,并缩小了它们的应用范围。
二、DySample概述
DySample是一种快速、有效且通用的动态上采样器,其主要概念是从点采样的角度来设计上采样过程,而不是传统的基于内核的动态上采样方法。DySample通过生成上采样位置而非内核,显著减少了计算资源的消耗,并且不需要定制的CUDA包。与其他动态上采样器相比,DySample在延迟(latency)、训练内存(memory)、训练时间(training time)、浮点运算次数(GFLOPs)和参数量(parameters)等方面表现出更高的效率。在本文测试DySample上采样模块的过程中,首先从一个简单的实现开始,然后通过不断调整公式和参数等逐步改进其性能。
三、不同上采样器比较
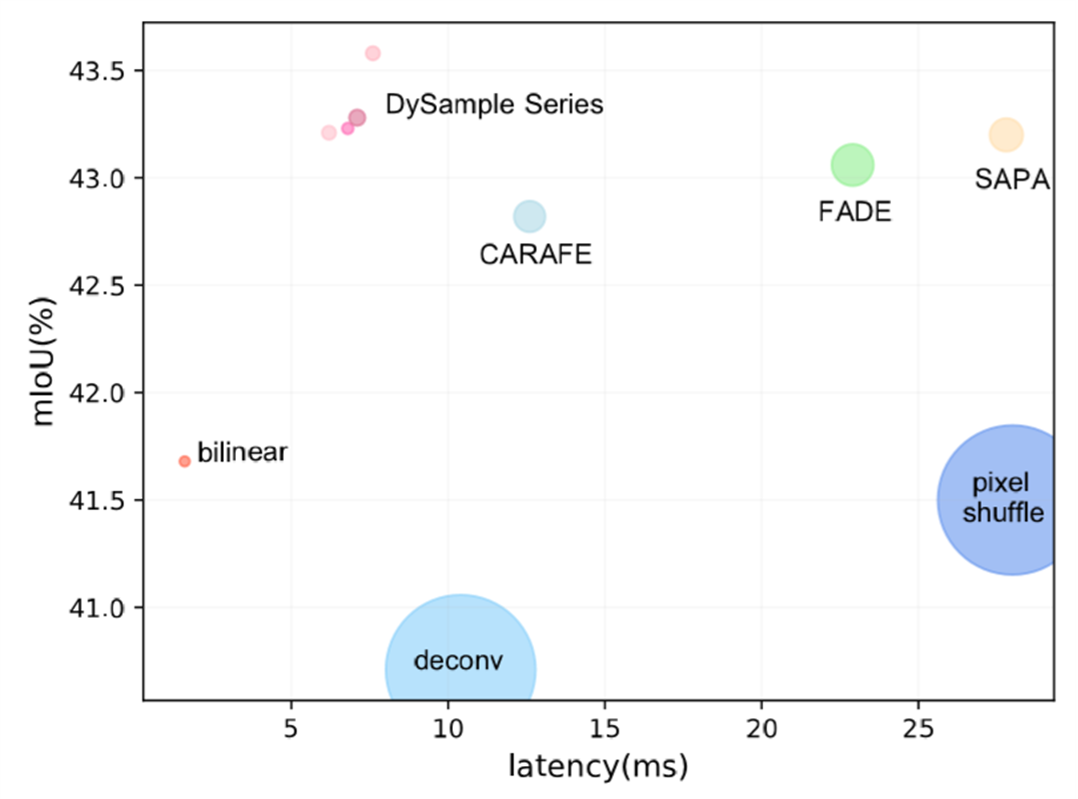
- 该图是对不同上采样器的性能、推理速度和
GFLOPs进行比较。 - 圆圈大小表示
GFLOPs成本。 通过将大小为256×120×120的特征图进行×2 上采样来测试推理时间。 - 在大型室内场景
ADE20K数据集上使用SegFormer-B1模型。 - 测试平均交并比(
mIoU)性能和额外增加的GFLOPs。
四、整体架构
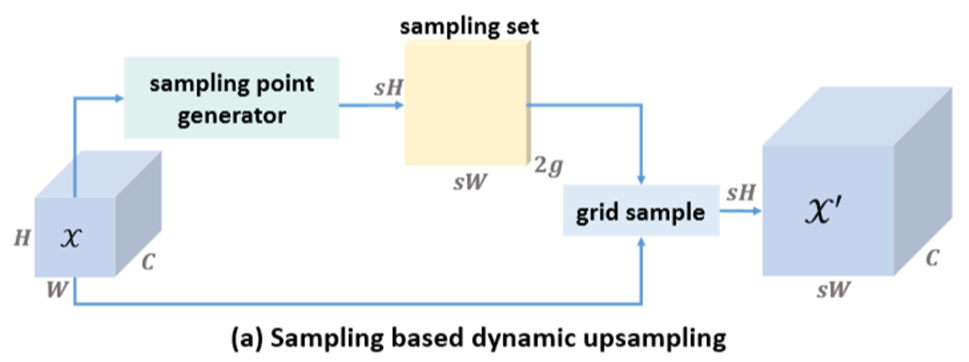
与近期基于内核的上采样器不同,我们将上采样的本质理解为点重采样。在DySample中,有着基于动态上采样和模块设计的采样过程。其中输入特征X 、上采样特征X‘ 、生成偏移量O,原始采样网络G,采样集S。
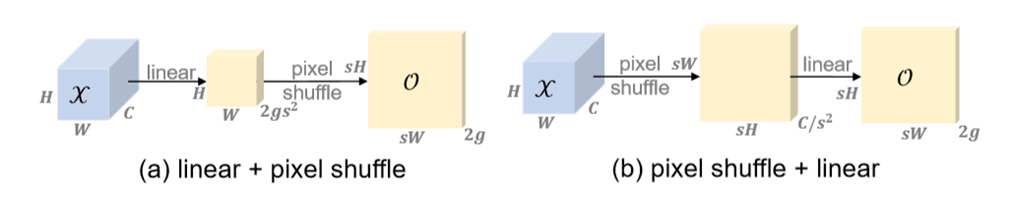
- (a)图:采样集
S由采样点生成器生成,通过网格采样函数对输入特征进行重新采样。
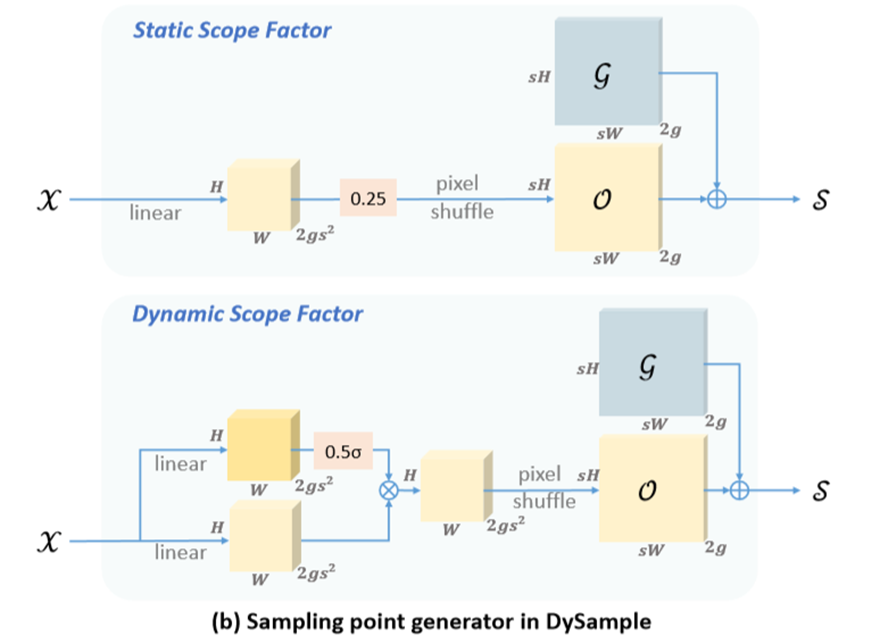
- (b)图:采样集
S=生成偏移量O+原始采样网络G。 上框表示具有静态范围因子的版本,其中偏移量通过线性层生成。下框描述具有动态范围因子的版本,其中先生成一个范围因子,然后用它来调制偏移量。σ表示Sigmoid函数。
五、设计过程
(1)初步设计
- 变量注释:输入特征
X、上采样特征X‘、生成偏移量O,原始网格G,采样集S
X ′ = grid_sample ( X , S ) . (1) X' = \text{grid\_sample}(X, S).\tag{1} X′=grid_sample(X,S).(1)
O = linear ( X ) , (2) O = \text{linear}(X),\tag{2} O=linear(X),(2)
S = G + O , (3) S = G + O,\tag{3} S=G+O,(3)
- 目标检测:
Faster R-CNN(DySample) : 37.9%的AP,Faster R-CNN(CARAFE):38.6%的AP。 - 语义分割:
SegFormer-B1(DySample) 获得了41.9%的mIoU,SegFormer-B1(CARAFE)
42.8%的mIoU。
(2)第一次修改
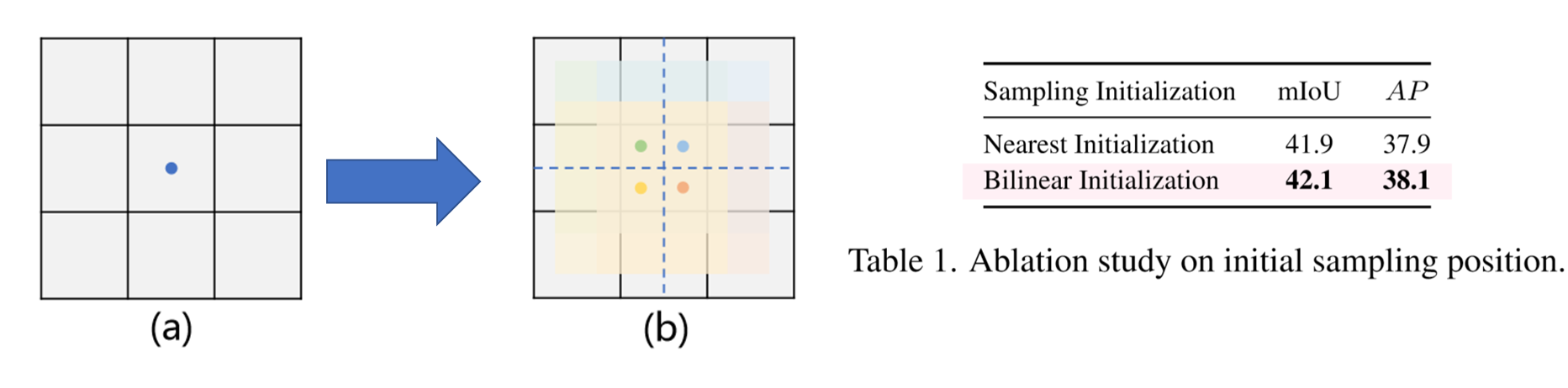
- 点和彩色掩码分别表示初始采样位置和偏移范围;
- 本次示例,我们考虑采样四个点。
- (a)在
Nearest Initialization的情况下,四个偏移量共享相同的初始位置,这会导致初始采样位置分布不均匀; - (b)在
Bilinear Initialization的情况下,我们将初始位置分开,使他们的初始采样位置分布均匀。
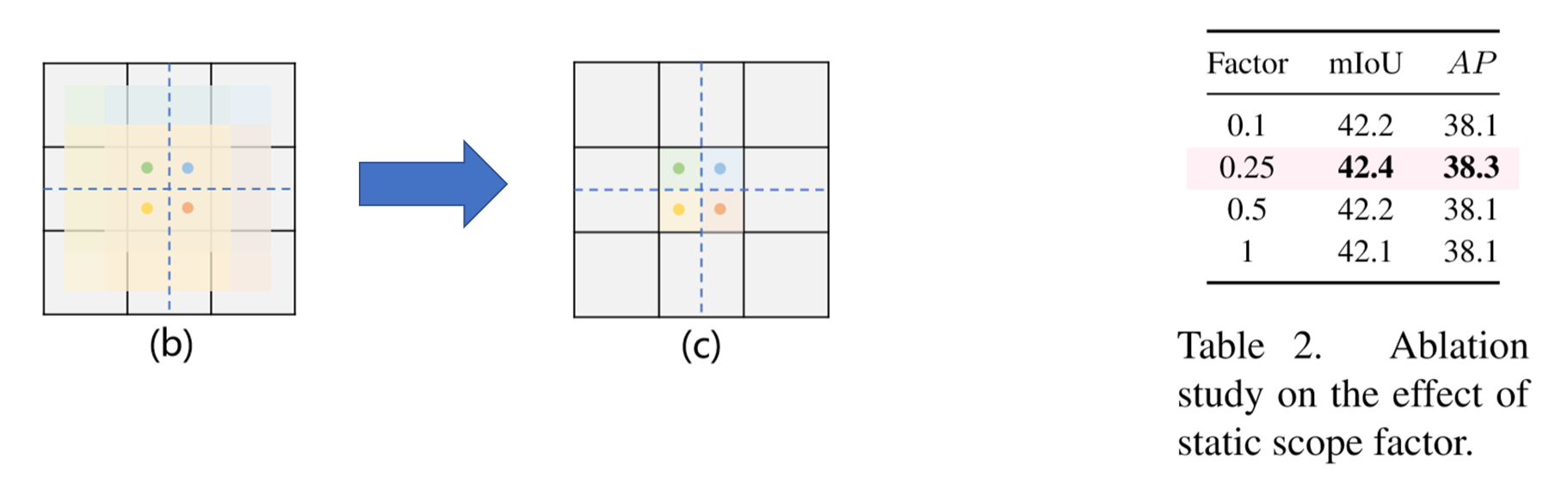
(3)第二次修改
我们发现,当(b)在没有偏移调制的情况下,偏移范围通常会重叠,所以在(c)中,我们局部约束偏移范围以减少重叠。
我们重写公式(2),通过不断实验确定静态范围因子为0.25时DySample达到最优效果
O
=
0.25
×
linear
(
X
)
(4)
O = 0.25 \times \text{linear}(X) \tag{4}
O=0.25×linear(X)(4)
(4)第三次修改
然而,乘以静态范围因子是重叠问题的一种软解法,这种方法无法完全解决问题。
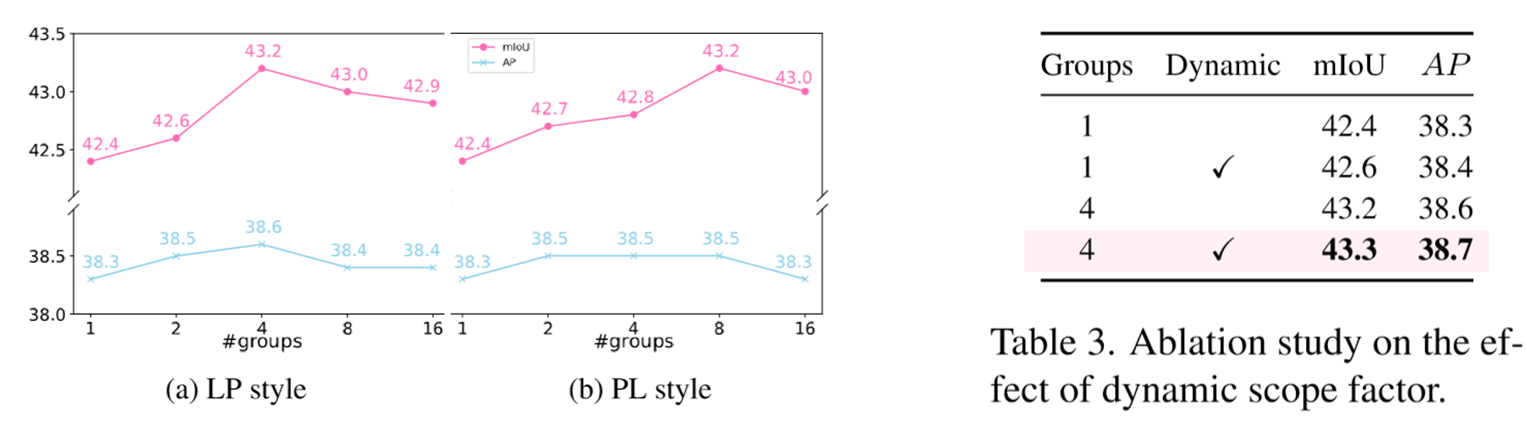
最终我们引入动态范围因子,重写公式(4),并且通过不断实验确定分组卷积个数为g=4时DySample达到最优效果。
O
=
0.5
⋅
sigmoid
(
linear
1
(
X
)
)
⋅
linear
2
(
X
)
(5)
O = 0.5 \cdot \text{sigmoid}(\text{linear}_1(X)) \cdot \text{linear}_2(X) \tag{5}
O=0.5⋅sigmoid(linear1(X))⋅linear2(X)(5)
通过第三次修改,DySample应用在Faster R-CNN 和SegFormer-B1 的效果超过CARAFE。
六、DySample四种变体
DySample系列。根据范围因子的形式(静态/动态)和偏移生成样式(LP/PL),我们研究了四种变体:
DySample:具有静态范围因子的LP风格;DySample+:具有动态范围因子的LP风格;DySample-S:具有静态范围因子的PL风格;DySample-S+:具有动态范围因子的PL风格。
其中LP和PL即采样点生成器(Sampling Point Generator)中线性层和像素重排层的顺序:
七、复杂性分析
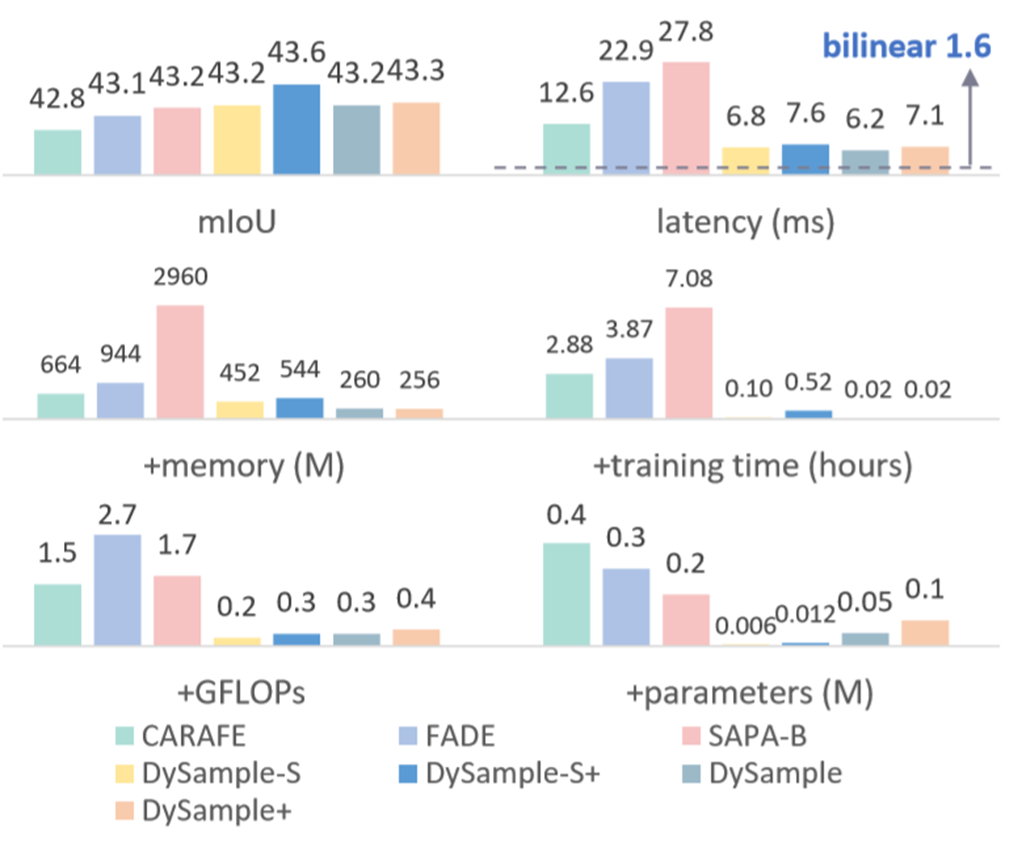
从图中可以就看出,DySample在延迟(latency)、训练内存(memory)、训练时间(training time)、浮点运算次数(GFLOPs)和参数量(parameters)等方面表现出更高的效率。
需要注意的是:
- 虽然
LP所需的参数比PL多,但前者更灵活,内存占用更小,推理速度更快; S版本在参数和GFLOPs方面的成本更低,但内存占用和延迟更大,因为PL需要额外的存储。+版本也增加了一些计算量。
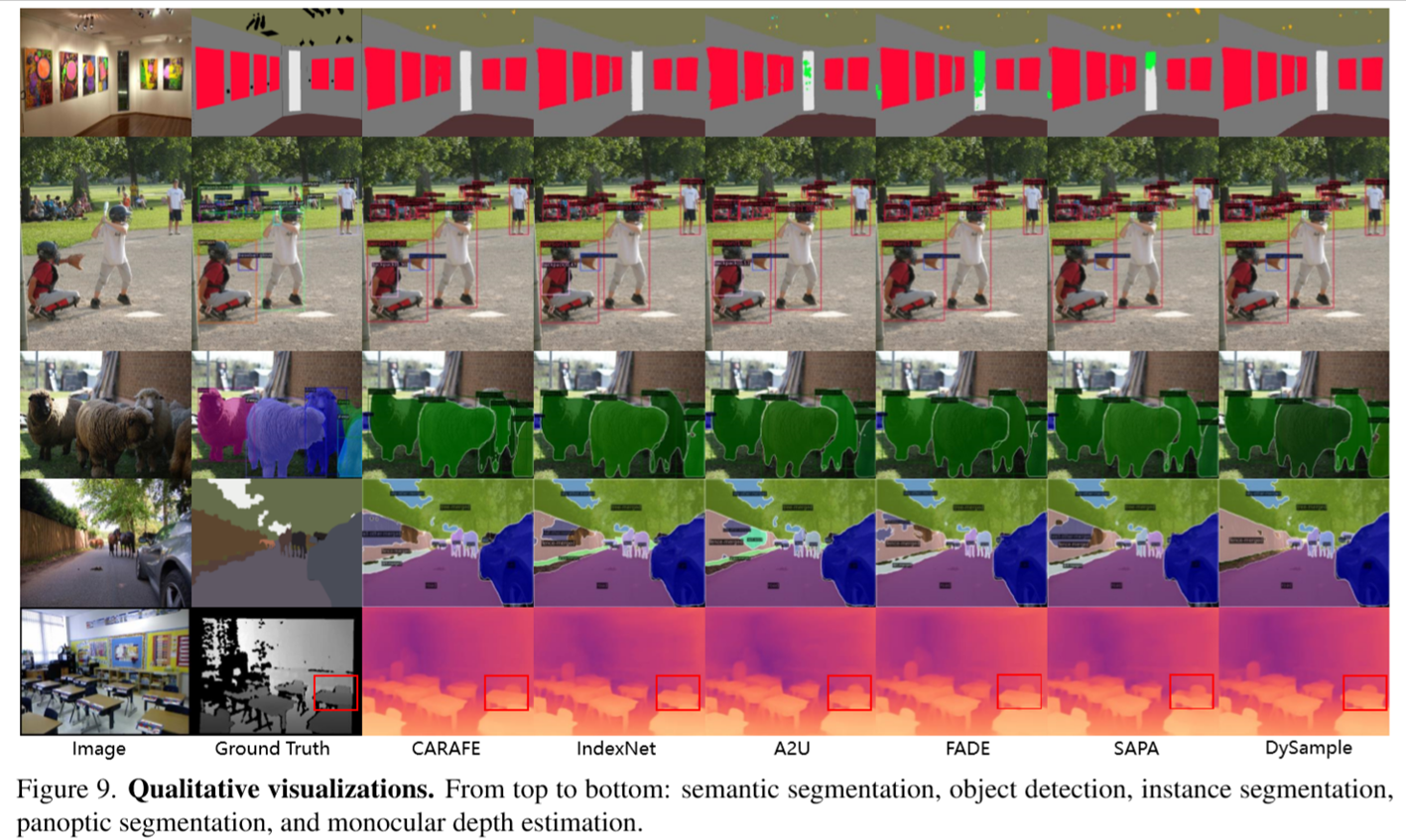
八、定性可视化
九、对比实验分析
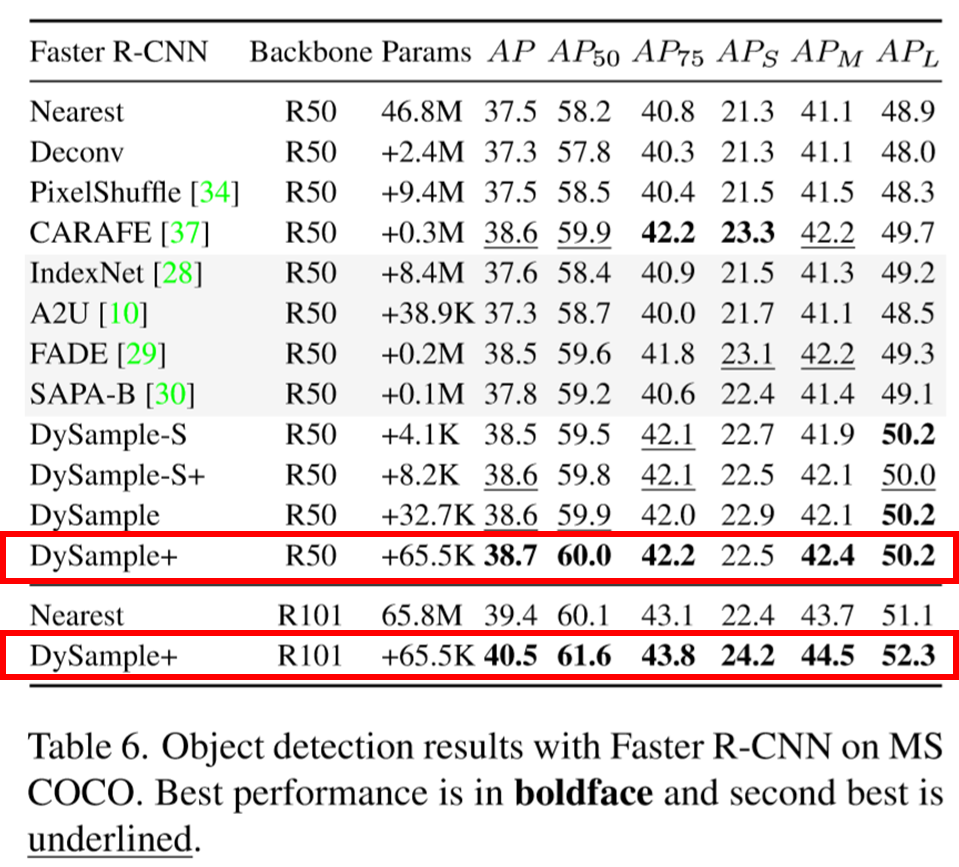
此处仅展示目标检测领域,该实验使用Faster R-CNN在MSCOCO数据集上进行对比实验
可以看出DySample+版本在Backbone为R50和R101时均保持最优检测性能
十、DySample代码分析
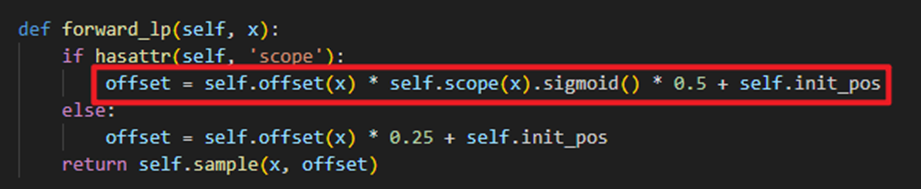
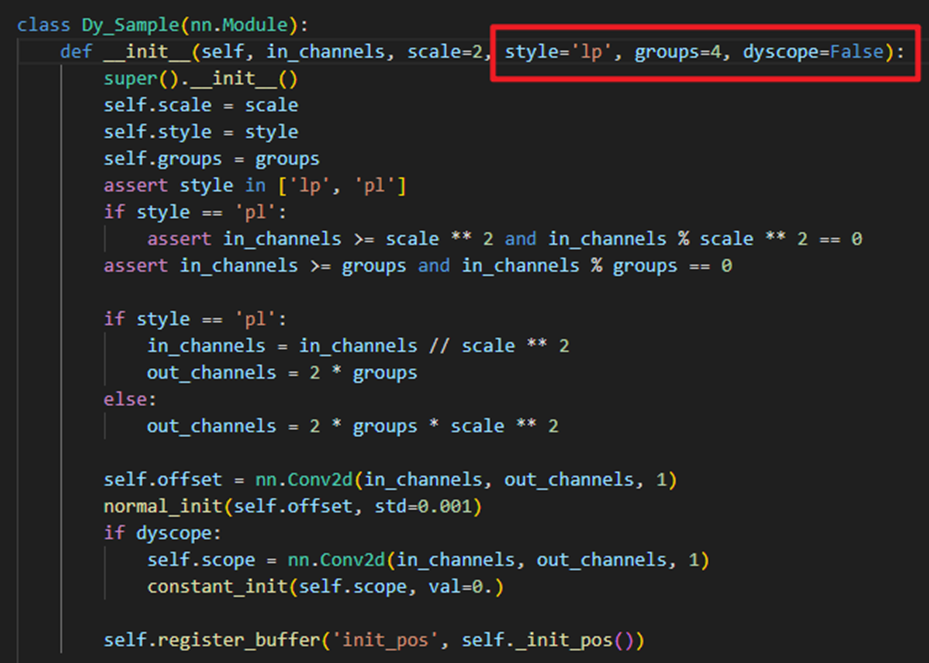
上述代码就是公式(5)的具体实现
O
=
0.5
⋅
sigmoid
(
linear
1
(
X
)
)
⋅
linear
2
(
X
)
(5)
O = 0.5 \cdot \text{sigmoid}(\text{linear}_1(X)) \cdot \text{linear}_2(X) \tag{5}
O=0.5⋅sigmoid(linear1(X))⋅linear2(X)(5)
style参数定义了上采样的风格(LP/PL)groups参数用于分组卷积g的个数dyscope参数是用于确定是否使用动态范围因子(+)- 此代码代表默认的第一种
DySample
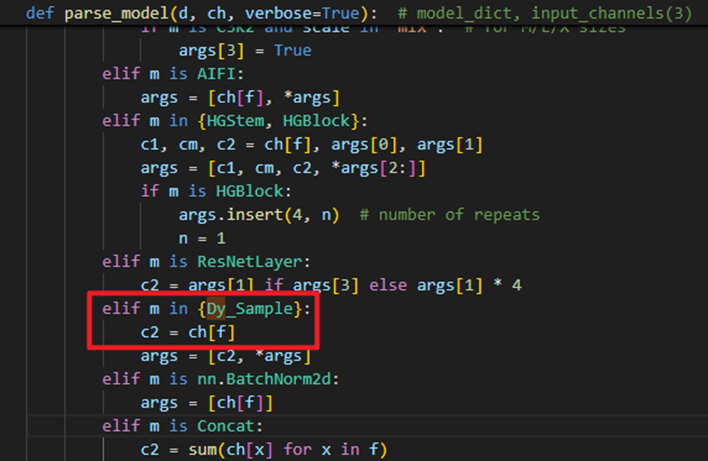
在Ultralytics封装的YOLO系列中,DySample部署模块时的task.py如下图所示