6.4 牛顿类算法

梯度法仅仅依赖函数值和梯度的信息（即一阶信息），当 ${\nabla }^{2}f(x)$ 的条件数较大时，它的收敛速度比较缓慢。如果 $f(x)$ 充分光滑，则可以利用二阶导数信息构造下降方向 $d^k$，可以加速算法的迭代。牛顿类算法就是利用二阶导数信息来构造迭代格式的算法。由于利用的信息变多，牛顿法的实际表现可以远好于梯度法，但是它对函数 $f(x)$ 的要求也相应变高。本节首先介绍经典牛顿法的构造和性质，然后介绍一些修正的牛顿法和实际应用。

6.4.1 经典牛顿法

对二次连续可微函数 $f(x)$，考虑 $f(x)$ 在迭代点 $x^k$ 处的二阶泰勒展开
$$f(x^k+d^k)=f(x^k)+\nabla f(x^k{)}^{\text{T}}{d}^k+\frac{1}{2}(d^k{)}^{\text{T}}{\nabla }^{2}f(x^k)d^k+o(\Vert d^k{\Vert }^2)(\mathrm{6.4.1})$$

我们的目的是根据这个二阶近似来选取合适的下降方向 $d^k$。如果忽略高阶项 $o(\Vert d^k{\Vert }^2)$，并将等式右边看成关于 $d^k$ 的函数求其稳定点，可以得到

$${\nabla }^{2}f(x^k)d^k=-\nabla f(x^k)(\mathrm{6.4.2})$$

方程 (6.4.2) 也被称为牛顿方程，$d^k$ 被称为牛顿方向。若 ${\nabla }^{2}f(x^k)$ 非奇异，那么更新方向 $d^k=-{\nabla }^{2}f(x^k{)}^{-1}\nabla f(x^k)$。因此经典牛顿法的更新格式为

$$x^{k+1}=x^k-{\nabla }^{2}f(x^k{)}^{-1}\nabla f(x^k)(\mathrm{6.4.3})$$

注意，在格式 (6.4.3) 中，步长 ${\alpha }_k$ 恒为 1，即可以不额外考虑步长的选取。我们也称步长为 1 的牛顿法为经典牛顿法。

6.4.2 收敛性分析

经典牛顿法 (6.4.3) 有很好的局部收敛性质。实际上我们有如下定理：

定理 6.6 (经典牛顿法的收敛性) 假设目标函数 $f$ 是二阶连续可微的函数，且海瑟矩阵在最优值点 $x^{\ast }$ 的一个邻域 $N_{\delta }(x^{\ast })$ 内是利普希茨连续的，即存在常数 $L>0$ 使得
$$\Vert {\nabla }^{2}f(x)-{\nabla }^{2}f(y)\Vert ⩽L\Vert x-y\Vert ,\forall x,y\in N_{\delta }(x^{\ast })$$

如果函数 $f(x)$ 在点 $x^{\ast }$ 处满足 $\nabla f(x^{\ast })=0,{\nabla }^{2}f(x^{\ast })\succ 0$，则对于迭代法 (6.4.3) 有如下结论：
(1) 如果初始点离 $x^{\ast }$ 足够近，则牛顿法产生的迭代点列 { x k } \{x^k\} {xk} 收敛到 $x^{\ast }$；
(2) { x k } \{x^k\} {xk} 收敛到 $x^{\ast }$ 的速度是 Q-二次的；
(3) { ∥ ∇ f ( x k ) ∥ } \{\|\nabla f(x^k)\|\} {∥∇f(xk)∥}Q-二次收敛到 0.

证明 从牛顿法的定义 (6.4.3) 和最优值点 $x^{\ast }$ 的性质 $\nabla f(x^{\ast })=0$ 可得
$$\begin{array}{rl}{x}^{k+1}-x^{\ast }& =x^k-{\nabla }^{2}f(x^k{)}^{-1}\nabla f(x^k)-x^{\ast }\\ & ={\nabla }^{2}f(x^k{)}^{-1}[{\nabla }^{2}f(x^k)(x^k-x^{\ast })-(\nabla f(x^k)-\nabla f(x^{\ast }))].\end{array}(\mathrm{6.4.4})$$

根据泰勒公式，可得
$$\nabla f(x^k)-\nabla f(x^{\ast })={\int }_0^1{\nabla }^{2}f(x^k+t(x^{\ast }-x^k))(x^k-x^{\ast })\mathrm{d}t$$

因此有估计
$$\begin{array}{rl}& \begin{array}{r}\Vert {\nabla }^{2}f(x^k)(x^k-x^{\ast })-(\nabla f(x^k)-\nabla f(x^{\ast }))\Vert \end{array}\\ & =\Vert {\int }_0^1[{\nabla }^{2}f(x^k+t(x^{\ast }-x^k))-{\nabla }^{2}f(x^k)](x^k-x^{\ast })\mathrm{d}t\Vert \\ & ⩽\begin{array}{r}{\int }_0^1\Vert {\nabla }^{2}f(x^k+t(x^{\ast }-x^k))-{\nabla }^{2}f(x^k)\Vert \Vert x^k-x^{\ast }\Vert \mathrm{d}t\end{array}\\ & ⩽\Vert x^k-x^{\ast }{\Vert }^2{\int }_0^{1}Lt\mathrm{d}t\\ & =\frac{L}{2}\Vert x^k-x^{\ast }{\Vert }^2\end{array}(\mathrm{6.4.5})$$

其中第二个不等式是由于海瑟矩阵的局部利普希茨连续性。又因为 ${\nabla }^{2}f(x^{\ast })$ 是非奇异的且 $f$ 二阶连续可微，因此存在 $r$ , 使得对任意满足 $\Vert x-x^{\ast }\Vert ⩽r$ 的点 $x$ 均有 $\Vert {\nabla }^{2}f(x{)}^{-}1\Vert ⩽2\Vert {\nabla }^{2}f(x^{\ast }{)}^{-1}\Vert$。结合 (6.4.4) 式与 (6.4.5) 式可得：
$$\begin{array}{rl}& \Vert x^{k+1}-x^{\ast }\Vert \\ & ⩽\Vert {\nabla }^{2}f(x^k{)}^{-1}\Vert \Vert {\nabla }^{2}f(x^k)(x^k-x^{\ast })-(\nabla f(x^k)-\nabla f(x^{\ast }))\Vert \\ & ⩽L\Vert {\nabla }^{2}f(x^{\ast }{)}^{-1}\Vert \Vert x^k-x^{\ast }{\Vert }^2\end{array}(\mathrm{6.4.6})$$

因此，当初始点 $x^0$ 满足
$$\Vert x^0-x^{\ast }\Vert ⩽\min \left\{\delta ,r,\frac{1}{2L\Vert {\nabla }^{2}f(x^{\ast }{)}^{-1}\Vert }\right\}\stackrel{\mathrm{def}}{=}\hat{\delta }$$

时，可保证迭代点列一直处于邻域 $N_{\hat{\delta }}(x^{\ast })$ 中，因此 { x k } \{x^k\} {xk} 是 Q-二次收敛到 $x^{\ast }$。
由牛顿方程 (6.4.2) 可知
$$\begin{array}{rl}\Vert \nabla f(x^{k+1})\Vert & =\Vert \nabla f(x^{k+1})-\nabla f(x^k)-{\nabla }^{2}f(x^k)d^k\Vert \\ & =\Vert {\int }_0^1{\nabla }^{2}f(x^k+t{d}^k)d^{k}dt-{\nabla }^{2}f(x^k)d^k\Vert \\ & ⩽{\int }_0^1\Vert {\nabla }^{2}f(x^k+t{d}^k)-{\nabla }^{2}f(x^k)\Vert \Vert d^k\Vert dt\\ & ⩽\frac{L}{2}\Vert d^k{\Vert }^2⩽\frac{1}{2}L\Vert {\nabla }^{2}f(x^k{)}^{-1}{\Vert }^2\Vert \nabla f(x^k){\Vert }^2\\ & ⩽2L\Vert {\nabla }^{2}f(x^{\ast }{)}^{-1}{\Vert }^2\Vert \nabla f(x^k){\Vert }^2\end{array}(\mathrm{6.4.7})$$

这证明了梯度的范数 Q-二次收敛到0。

定理 6.6 表明经典牛顿法是收敛速度很快的算法，但它的收敛是有条件的：第一，初始点 $x^0$ 必须距离问题的解充分近，即牛顿法只有局部收敛性；第二，海瑟矩阵 ${\nabla }^{2}f(x^{\ast })$ 需要为正定矩阵，有例子表明，若 ${\nabla }^{2}f(x^{\ast })$ 是奇异的半正定矩阵，牛顿算法的收敛速度可能仅达到 Q-线性。问题的条件数并不会在很大程度上影响牛顿法的收敛速度，利普希茨常数 $L$ 在迭代后期通常会被 $\Vert x^k-x^{\ast }\Vert$ 抵消。但对于病态问题，牛顿法的收敛域可能会变小，这对初值选取有了更高的要求。

以上总结了牛顿法的特点，我们可以知道牛顿法适用于优化问题的高精度求解，但它没有全局收敛性质。因此在实际应用中，人们通常会使用梯度类算法先求得较低精度的解，而后调用牛顿法来获得高精度的解。

6.4.3 修正牛顿法

经典牛顿法有如下缺陷：
(1) 每一步迭代需要求解一个 $n$ 维线性方程组，这导致在高维问题中计算量很大。海瑟矩阵 ${\nabla }^{2}f(x^k)$ 既不容易计算又不容易储存。
(2) 当 ${\nabla }^{2}f(x^k)$ 不正定时，由牛顿方程 (6.4.2) 给出的解 $d^k$ 的性质通常比较差。例如可以验证当海瑟矩阵正定时，$d^k$ 是一个下降方向，而在其他情况下 $d^k$ 不一定为下降方向。
(3) 当迭代点距最优值较远时，直接选取步长 ${\alpha }_k=1$(固定步长)会使得迭代极其不稳定，在有些情况下迭代点列会发散。

为了克服这些缺陷，我们必须对经典牛顿法做出某种修正或变形，使其成为真正可以使用的算法。这里介绍带线搜索的修正牛顿法，其基本思想是对牛顿方程中的海瑟矩阵 ${\nabla }^{2}f(x^k)$ 进行修正，使其变成正定矩阵；同时引入线搜索以改善算法稳定性。它的一般框架见算法 6.3。该算法的关键在于修正矩阵 $E^k$ 如何选取。一个最直接的取法是取 $E^k={\tau }_{k}I$，即取 $E^k$ 为单位矩阵的常数倍。根据矩阵理论可以知道，当 ${\tau }_k$ 充分大时，总可以保证 $B^k$ 是正定矩阵。然而 ${\tau }_k$ 不宜取得过大，这是因为当 ${\tau }_k$ 趋于无穷时，$d^k$ 的方向会接近负梯度方向。比较合适的取法是先估计 ${\nabla }^{2}f(x^k)$ 的最小特征值，再适当选择 ${\tau }_k$。

# 算法 6.3 带线搜索的修正牛顿法
import numpy as np
import matplotlib.pyplot as plt
# 计算alpha的三种线搜索准则
def line_search_Armijo(x, alpha_hat, d, c1, gamma = 0.5):
    t = 0
    alpha = alpha_hat
    while (f(x + alpha * d) > f(x) + c1 * alpha * np.dot(grad_f(x), d)):
        alpha = gamma * alpha
        t = t + 1
    return alpha, t
def line_search_Goldstein(x, alpha_hat, d, c, gamma = 0.5):
    t = 0
    alpha = alpha_hat
    while (f(x + alpha * d) > f(x) + c * alpha * np.dot(grad_f(x), d)) and (grad_f(x + alpha * d) < (f(x) + (1-c) * alpha * np.dot(grad_f(x), d))):
        alpha = gamma * alpha
        t = t + 1
    return alpha, t
def line_search_Wolf(x, alpha_hat, d, gamma = 0.5, c1 = 0.1, c2 = 0.9):
    t = 0
    alpha = alpha_hat
    while (f(x + alpha * d) > f(x) + c1 * alpha * np.dot(grad_f(x), d)) and (grad_f(x + alpha * d) < c2 * np.dot(grad_f(x), d)) :
        alpha = gamma * alpha
        t = t + 1
    return alpha, t

def modified_newton_method(x0, alpha, c, gamma, max_iter=1000, tol=1e-6):
    x = x0
    x_history = [x]
    for k in range(max_iter):
        Ek = np.eye(len(x)) * np.abs(np.min(np.linalg.eigvals(hess_f(x))))
        B = hess_f(x) + Ek
        d = np.linalg.solve(B, -grad_f(x))
        # Armijo线搜索准则
        alpha, _ = line_search_Armijo(x, alpha, d, c, gamma)
        x = x + alpha * d
        x_history.append(x)
        if np.linalg.norm(grad_f(x)) < tol: # 判断当前点梯度的范数是否小于阈值 tol
            break
    return x_history, k

# 示例函数及其梯度、海瑟矩阵的计算
def f(x):
    return x[0]**2 + 10 * x[1]**2
def grad_f(x):
    return np.array([2*x[0], 20*x[1]])
def hess_f(x):
    return np.array([[2, 0], [0, 20]])

# 初始点
x0 = np.array([-10, -1])
alpha = 0.085
c = 0.1
gamma = 0.5
# 调用修正牛顿法
M_Newton_history, k = modified_newton_method(x0, alpha, c, gamma)
print("Optimal solution:", M_Newton_history[-1])
'''Optimal solution: [-4.80670716e-07 -2.80842320e-14]'''
print("迭代次数：", k)
'''迭代次数： 387'''
# 绘制等高线图
x = np.linspace(-12, 12, 100)
y = np.linspace(-4, 4, 100)
X, Y = np.meshgrid(x, y)
Z = X**2 + 10*Y**2 

plt.figure(figsize=(10, 5))
plt.contour(X, Y, Z, levels=np.logspace(-2, 3, 20), cmap='jet')  # levels 参数控制等高线的密集程度
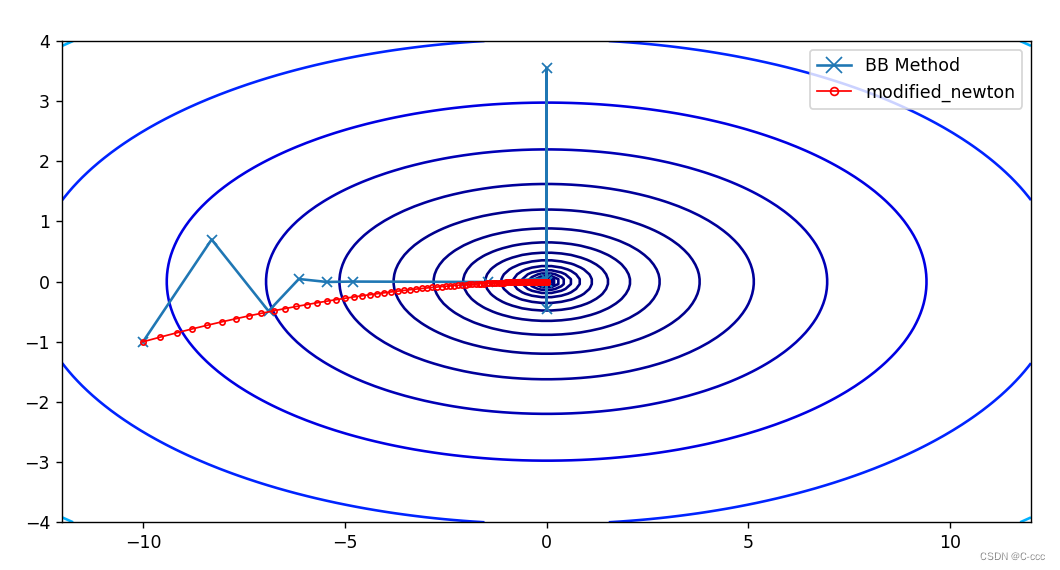
plt.plot([x[0] for x in bb_history], [x[1] for x in bb_history], marker='x', label='BB Method')  # 添加优化路径
plt.plot([x[0] for x in M_Newton_history], [x[1] for x in M_Newton_history], markersize = 3, marker='o', markerfacecolor='none', linewidth=1, color='r', label='modified_newton')
plt.legend(loc='best', markerscale=1.5)  # 设置标签位置为最佳位置，调整图例的大小
plt.show()

另一种 $E^k$ 的选取是隐式的，它是通过修正 Cholesky 分解的方式来求解牛顿方程$\nabla^{2}f(x{k})d^{k}=-\nabla f(x^{k})(6.4.2)
$。当海瑟矩阵正定时，方程组 (6.4.2) 可以用 Cholesky 分解快速求解。当海瑟矩阵不定或条件数较大时，Cholesky 分解会失败。而修正 Cholesky 分解算法对基本 Cholesky 分解算法进行修正，且修正后的分解和原矩阵相差不大。首先回顾 Cholesky 分解的定义，对任意对称正定矩阵 $A=(a_{ij})$，它的 Cholesky 分解可写作

$$A=LD{L}^{\mathrm{T}}$$

其中 $L=(l_{ij})$ 是对角线元素均为 1 的下三角矩阵，$D=Diag(d_1,d_2,\cdots ,d_n)$ 是对角矩阵且对角线元素均为正。在算法 6.4 中直接给出基本的 Cholesky 分解算法。

# 算法 6.4 Cholesky 分解
import numpy as np
def cholesky_decomposition(A):
    n = A.shape[0]
    L = np.zeros((n, n))
    D = np.zeros((n, n))
    for j in range(n):
        c_jj = A[j, j] - np.sum(D[:j, j] * L[j, :j]**2)
        d_j = c_jj
        D[j, j] = d_j
        L[j, j] = 1.0
        for i in range(j+1, n):
            c_ij = A[i, j] - np.sum(D[:j, j] * L[i, :j] * L[j, :j])
            l_ij = c_ij / d_j
            L[i, j] = l_ij
    return L, D

A = np.array([[4, 12, -16], [12, 37, -43], [-16, -43, 98]])
L, D = cholesky_decomposition(A)
print("L:", L)
'''[[ 1.          0.          0.        ]
 [ 3.          1.          0.        ]
 [-4.         -1.16216216  1.        ]]'''
print("D:", D)
'''[[ 4.  0.  0.]
 [ 0. 37.  0.]
 [ 0.  0. 98.]]'''

根据 Cholesky 分解的形式，如果 $A$ 正定且条件数较小，矩阵 $D$ 的对角线元素不应该太小，如果计算过程中发现 $d_j$ 过小就应该及时修正。同时我们需要保证该修正是有界的，因此对修正后的矩阵元素也需要有上界约束。具体来说，我们选取两个正参数 $\delta ,\beta$ 使得

$$d_j⩾\delta ,l_{ij}\sqrt{d_j}⩽\beta ,i=j+1,j+2,\cdots ,n.$$

在算法 6.4 中，我们只需要修改对 $d_j$ 的更新即可保证上述条件成立。具体更新方式为

$$d_j=\max \left\{|c_{jj}|,{\left(\frac{{\theta }_j}{\beta }\right)}^2,\delta \right\},{\theta }_j=\underset{i>j}{\max }|c_{ij}|$$

可以证明，修正的 Cholesky 分解算法实际上是计算修正矩阵 ${\nabla }^{2}f(x^k)+E^k$ 的 Cholesky 分解，其中 $E^k$ 是对角矩阵且对角线元素非负。当 ${\nabla }^{2}f(x^k)$ 正定且条件数足够小时有 $E^k=0$。

# 修正的cholesky分解 修正牛顿法
import numpy as np
import matplotlib.pyplot as plt
def modified_cholesky_decomposition(A, delta, beta):
    n = A.shape[0]
    L = np.zeros((n, n))
    D = np.zeros((n, n))
    for j in range(n):
        c_jj = A[j, j] - np.sum(D[:j, j] * L[j, :j]**2)
        if j == n - 1:
            theta_j = np.abs(A[j, j])
        else:
            theta_j = max(np.abs(A[j, j]), np.max(np.abs(A[j, j+1:])))

        d_j = max(np.abs(c_jj), (theta_j / beta)**2, delta)
        D[j] = d_j
        L[j, j] = 1.0
        for i in range(j+1, n):
            c_ij = A[i, j] - np.sum(D[:j, j] * L[i, :j] * L[j, :j])
            l_ij = c_ij / d_j
            L[i, j] = l_ij
    return L, D

def modified_newton_method(x0, delta, beta, max_iter=100, tol=1e-6):
    x = x0
    x_history = [x]
    k = 0
    while k <= max_iter:
        L, D = modified_cholesky_decomposition(hess_f(x), delta, beta)
        d = np.linalg.solve(L.T, np.linalg.solve(L, -grad_f(x)))
        gamma = 0.5
        alpha = 0.085
        c = 0.1
        while f(x + alpha * d) > f(x) + c * alpha * np.dot(grad_f(x), d):
            alpha = gamma * alpha
        x = x + alpha * d
        x_history.append(x)
        k = k + 1
        if np.linalg.norm(grad_f(x)) < tol:
            break
    return x_history, k

# 定义目标函数、梯度和海瑟矩阵函数
def f(x):
    return x[0]**2 + 10 * x[1]**2
def grad_f(x):
    return np.array([2*x[0], 20*x[1]])
def hess_f(x):
    return np.array([[2, 0], [0, 20]])

# 设置初始点 x0 和参数 delta、beta
x0 = np.array([-10, -1])
delta = 1e-4
beta = 1e-4
cholesky_newton_history, k = modified_newton_method(x0, delta, beta)
print("Optimal value:", cholesky_newton_history[-1])
'''Optimal value: [-4.32619814e-07  8.01533432e-15]'''
print("迭代次数:", k)
'''迭代次数: 91'''
# 绘制等高线图
x = np.linspace(-12, 12, 100)
y = np.linspace(-4, 4, 100)
X, Y = np.meshgrid(x, y)
Z = X**2 + 10*Y**2 
plt.figure(figsize=(10, 5))
plt.contour(X, Y, Z, levels=np.logspace(-2, 3, 20), cmap='jet')  # levels 参数控制等高线的密集程度
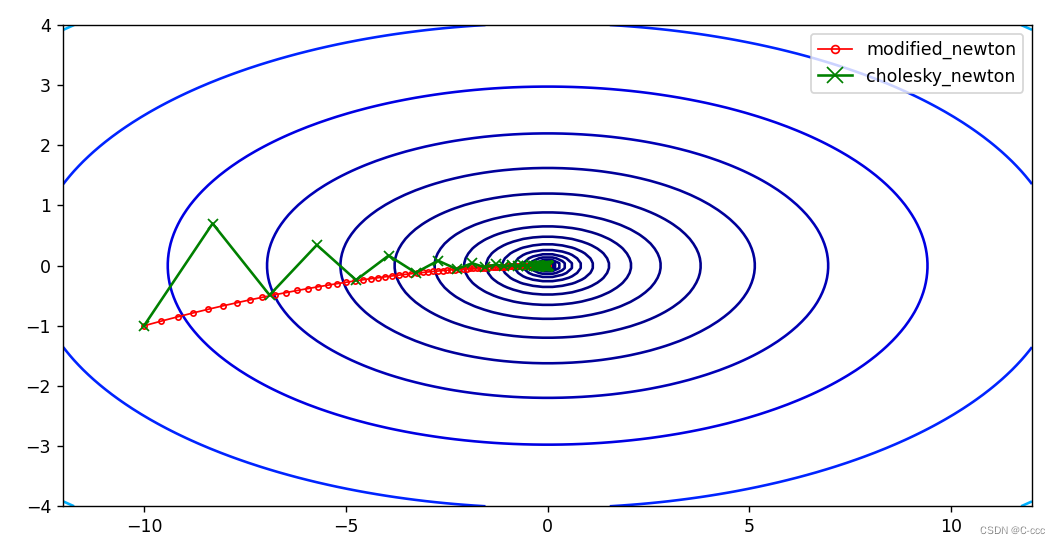
plt.plot([x[0] for x in M_Newton_history], [x[1] for x in M_Newton_history], markersize = 3, marker='o', markerfacecolor='none', linewidth=1, color='r', label='modified_newton')
plt.plot([x[0] for x in cholesky_newton_history], [x[1] for x in cholesky_newton_history],color='green', marker='x', label='cholesky_newton')
plt.legend(loc='best', markerscale=1.5)  # 设置标签位置为最佳位置，调整图例的大小
plt.show()

6.4.4 非精确牛顿法

在经典牛顿法中，计算牛顿方向 $d^k$ 依赖于求解线性方程组，当 $n$ 较大但 ${\nabla }^{2}f(x^k)$ 有稀疏结构时，需要通过迭代法求解牛顿方程。
应用在大规模参数的场合时，牛顿法有以下问题: 第一，参数规模大，可能数以亿计，直接使用牛顿法则存储和计算都存在困难；第二，无法存储海瑟矩阵，同时对海瑟矩阵做 Cholesky 分解的代价过高。为解决这些问题，我们引入非精确牛顿法，即通过解牛顿方程的形式以求出牛顿方向(非精确)。

考虑牛顿方程 ${\nabla }^{2}f(x^k)d^k=-\nabla f(x^k)$ 的非精确解 $d^k$，我们引入向量 $r^k$ 来表示残差，则非精确牛顿方向满足

$${\nabla }^{2}f(x^k)d^k=-\nabla f(x^k)+r^k(\mathrm{6.4.8})$$

这里假设相对误差 ${\eta }_k$ 满足

$$\Vert r^k\Vert ⩽{\eta }_k\Vert \nabla f(x^k)\Vert (\mathrm{6.4.9})$$

显然，牛顿法的收敛性依赖于相对误差 ${\eta }_k$ 的选取，直观上牛顿方程求解得越精确，非精确牛顿法的收敛性就越好。为此有如下的定理：

定理 6.7 (非精确牛顿法的收敛性) 设函数 $f(x)$ 二阶连续可微，且在最小值点 $x^{\ast }$ 处的海瑟矩阵正定，则在非精确牛顿法中，
(1) 若存在常数 $t<1$ 使得 ${\eta }_k$ 满足 $0<{\eta }_k<t,k=1,2,\cdots$，则该算法收敛速度是 Q-线性的；
(2) 若 $\underset{k\to \infty }{\lim }{\eta }_k=0$，则该算法收敛速度是 Q-超线性的；
(3) 若 ${\eta }_k=\mathcal{O}(\Vert \nabla f(x^k)\Vert )$，则该算法收敛速度是 Q-二次的.

定理 6.7 的直观含义是如果要达到更好的收敛性就必须使得牛顿方程求解更加精确。在一般迭代法中，算法的停机准则通常都会依赖于相对误差的大小。定理 6.7 的第一条表明我们完全可以将这个相对误差设置为固定值，算法依然有收敛性。和经典牛顿法相比，固定误差的非精确牛顿法仅仅有 Q-线性收敛性，但在病态问题上的表现很可能好于传统的梯度法。如果希望非精确牛顿法能有 Q-二次收敛速度，则在迭代后期牛顿方程必须求解足够精确，这在本质上和牛顿法并无差别。

常用的非精确牛顿法是牛顿共轭梯度法，即使用共轭梯度法求解 (6.4.2) 式。由于共轭梯度法在求解线性方程组方面有不错的表现，因此只需少数几步（有时可能只需要一步）迭代就可以达到定理 6.7 中第一条结论需要的条件。在多数问题上牛顿共轭梯度法都有较好的数值表现，该方法已经是求解优化问题不可少的优化工具。

共轭梯度法：
共轭梯度法是一种介于最速下降法和牛顿法之间的方法，它结合了最速下降法的简单性和牛顿法的快速收敛性。共轭梯度法利用目标函数的梯度信息来构造共轭方向，并沿着这些方向进行搜索。与最速下降法不同，共轭梯度法在选择搜索方向时考虑了之前迭代的信息，从而避免了在相同方向上的重复搜索。对于二次型函数，共轭梯度法具有有限步收敛性。在实际应用中，共轭梯度法常用于求解大型稀疏线性方程组。
计算共轭方向(Fletcher-Reeves 公式)：${\beta }_{k+1}^{FR}=\frac{r_{k+1}^{\mathrm{T}}{r}_{k+1}}{r_k^{\mathrm{T}}{r}_k}，d_{k+1}=r_{k+1}+{\beta }_{k+1}{d}_k$

参考教材：《最优化：建模、算法与理论》