目录
多重背包问题介绍和案例
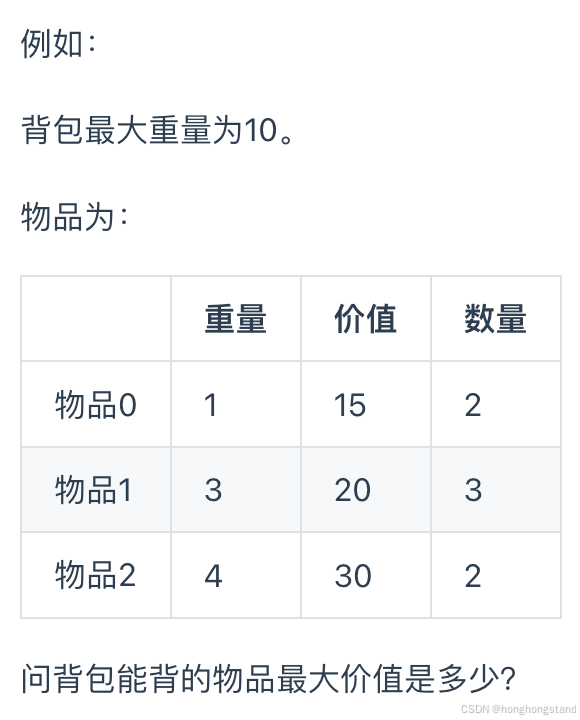
有N种物品和一个容量为V 的背包。第i种物品最多有Mi件可用,每件耗费的空间是Ci ,价值是Wi 。求解将哪些物品装入背包可使这些物品的耗费的空间 总和不超过背包容量,且价值总和最大。
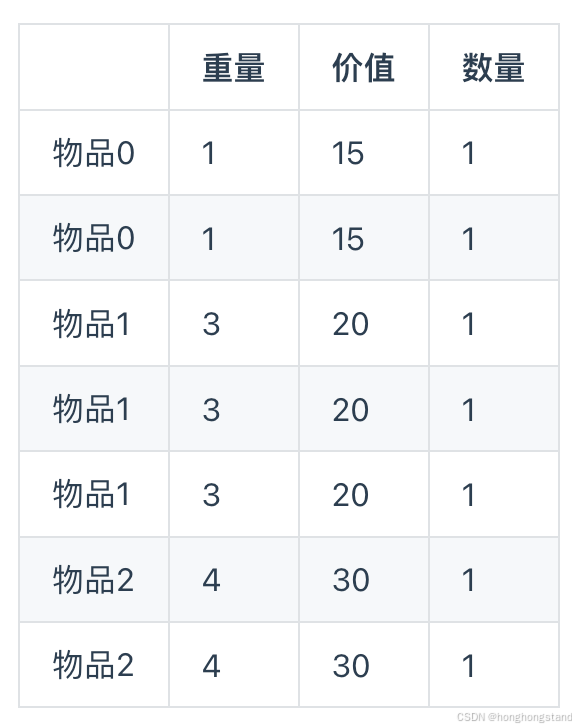
多重背包和01背包是非常像的, 为什么和01背包像呢?每件物品最多有Mi件可用,把Mi件摊开,其实就是一个01背包问题了。
因此,熟练掌握0-1背包,就能简单解决多重背包问题。这里对0-1背包进行一个复习,然后进入下一个阶段。
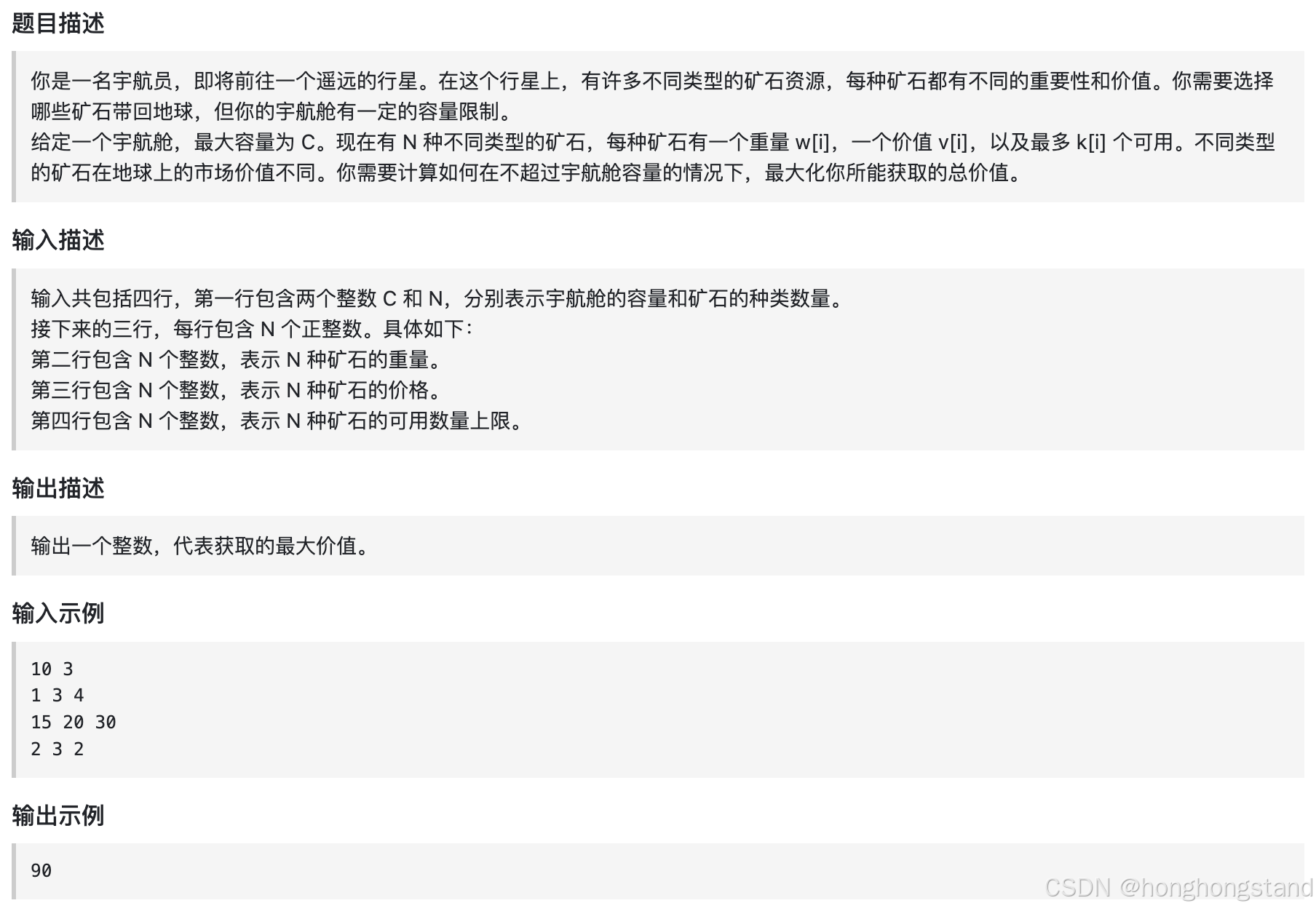
56. 携带矿石资源(第八期模拟笔试)
1. dp数组以及下标的含义
同 0 - 1 背包,dp[i][j] 表示使用第0 - i个物品装满容量为j的背包能取得的价值最多是多少
2. 状态转移方程
max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])
3. dp数组初始化
对第一行进行物品[0]价值的初始化,其他做全0初始化
4. 确定遍历顺序
一维dp时,背包容量需反向遍历,防止重复取物品
5. 实现
有两种处理方式,一种是按照思维逻辑,处理好输入,再运行0-1背包
def transform(weight_list, value_list, num_list):
weights, values = list(), list()
for idx, num in enumerate(num_list):
for _ in range(num):
weights.append(weight_list[idx])
values.append(value_list[idx])
length = len(weights)
return weights, values, length
while True:
try:
target, n = list(map(int, input().split(' ')))
weight_list = list(map(int, input().split()))
value_list = list(map(int, input().split()))
num_list = list(map(int, input().split()))
weight_list, value_list, n = transform(weight_list, value_list, num_list)
dp = [0] * (target + 1)
# print(dp)
for i in range(n):
for j in range(target, weight_list[i] - 1, -1):
dp[j] = max(dp[j], dp[j - weight_list[i]] + value_list[i])
print(dp[target])
except EOFError:
break另一种是直接在遍历过程中加入数量:
while True:
try:
C, N = input().split(" ")
C, N = int(C), int(N)
# value数组需要判断一下非空不然过不了
weights = [int(x) for x in input().split(" ")]
values = [int(x) for x in input().split(" ") if x]
nums = [int(x) for x in input().split(" ")]
dp = [0] * (C + 1)
for i in range(N):
# 遍历背包容量
for j in range(C, weights[i] - 1, -1):
for k in range(1, nums[i] + 1):
# 遍历 k,如果已经大于背包容量直接跳出循环
if k * weights[i] > j:
break
dp[j] = max(dp[j], dp[j - weights[i] * k] + values[i] * k)
print(dp[-1])
except EOFError:
break打家劫舍系列
198. 打家劫舍
1. dp数组以及下标的含义
走到下标[i] 能偷到的最大价值。
2. 状态转移方程
得到dp[i]的值,可以粗略归纳为偷 i 和不偷 i,即有dp[i - 2] (-1 不能偷) 和 dp[i - 1]。这里的思维点是,dp[i] 表示的是考虑到[i]位置时我们能偷到的最大价值。以最大价值来考虑,就不需要关注之前是跳几部取的,而是看状态转移规则就行了。
3. dp数组初始化
创建dp时多加一个边界位置,全0初始化即可;取nums时注意索引
4. 确定遍历顺序
正常顺序遍历
5. 实现
class Solution:
def rob(self, nums: List[int]) -> int:
n = len(nums)
dp = [0] * (n + 1)
for i in range(1, n + 1):
dp[i] = max(dp[i - 1], dp[i - 2] + nums[i - 1])
return dp[n]213. 打家劫舍 II
1. dp数组以及下标的含义
走到下标[i] 能偷到的最大价值。但是数组变成了环形数组。
2. 状态转移方程
和打家劫舍1的转移方程一致
3. dp数组初始化
创建dp时多加一个边界位置,全0初始化即可;取nums时注意索引
4. 确定遍历顺序
这个问题看似是环形数组,但实际上和环形数组的顺序关联不大。只需避免同时选头尾的问题即可。将输入数组拆分成[: -1]和[1: ]两个数组,使用dp获取每一个的最大值再进行比较即可。
5. 实现
class Solution:
def rob(self, nums: List[int]) -> int:
if len(nums) == 1:
return nums[0]
nums_1 = nums[: -1]
nums_2 = nums[1: ]
nums_list = [nums_1, nums_2]
max_value = 0
for num_list in nums_list:
dp = [0] * (len(num_list) + 1)
for i in range(1, len(num_list) + 1):
dp[i] = max(dp[i - 1], dp[i - 2] + num_list[i - 1])
value = dp[len(num_list)]
if value > max_value:
max_value = value
return max_value
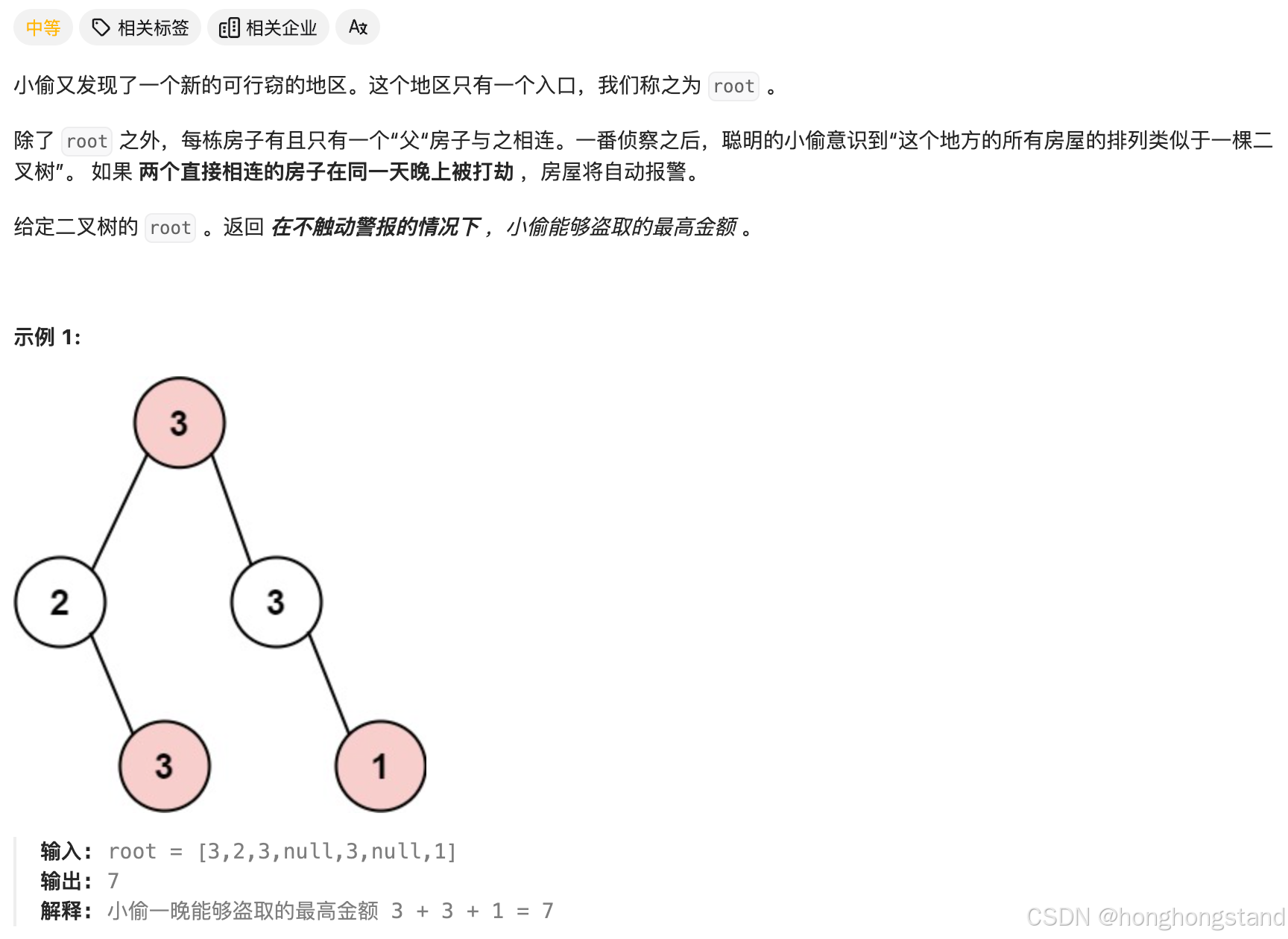
337. 打家劫舍 III
为了认识树形结构dp的特点,我们首先从暴力解法入手。
普通递归:
单步逻辑:
对于一个子二叉树,设置偷父节点和不偷父节点两个选择,之后,隔一层取一次,比较在子树上取父节点和不取父节点那种方案收益更大。
输入输出:
输入root,返回两个策略中偷到的更多的值
终止条件:
node 不存在时,退出并返回0值;node 是叶子结点时,返回节点值
实现:
代码逻辑非常直观,可以看到暴力搜索过程相当于模拟了全部取值的组合,结果正确但超时
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rob(self, root: Optional[TreeNode]) -> int:
if root is None:
return 0
if root.left is None and root.right is None:
return root.val
val_1 = root.val
if root.left:
val_1 += self.rob(root.left.left) + self.rob(root.left.right)
if root.right:
val_1 += self.rob(root.right.left) + self.rob(root.right.right)
val_2 = self.rob(root.left) + self.rob(root.right)
return max(val_1, val_2)记忆化递归:
上面的递归方法在测试例上只有两个没有通过,能不能通过空间换取时间呢?这就可以使用记忆化递归来解决。假设已经确定从某个节点出发的路径会被多次访问,那么我们可以直接讲这个节点的输出记录下来。新增终止条件:当访问到已经计算过的节点时,直接返回记录的返回值。使用python的字典可以很容易地进行优化。
实现:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
memory = dict()
def rob(self, root: Optional[TreeNode]) -> int:
if root is None:
return 0
if root.left is None and root.right is None:
return root.val
if self.memory.get(root) is not None:
return self.memory.get(root)
val_1 = root.val
if root.left:
val_1 += self.rob(root.left.left) + self.rob(root.left.right)
if root.right:
val_1 += self.rob(root.right.left) + self.rob(root.right.right)
val_2 = self.rob(root.left) + self.rob(root.right)
self.memory[root] = max(val_1, val_2)
return max(val_1, val_2)树状结构的动态规划
清楚两个递归遍历方法之后,可以来入门树形dp的思维和解法了。在树形dp中,算法架构依然是基于递归的,只是此前的递归中只关注计算结果,并没有记录每个节点的取值与否。
而动态规划是使用状态转移容器来记录状态的变化,这里可以使用一个长度为2的数组,记录当前节点偷与不偷所得到的的最大金钱。
想象成每个节点上挂一个一维len == 2 的dp数组,dp[0] 表示不取这个点的最大取值, dp[1] 表示取这个点得到的最大取值。
1. 输入输出和终止条件
传入根节点,返回长度为2的dp数组。遇到空节点终止。递归函数返回长度为2的数组
2. 单层递归逻辑
如果是偷当前节点,那么左右孩子就不能偷,val1 = cur.val + left[0] + right[0]; (如果对下标含义不理解就再回顾一下dp数组的含义)
如果不偷当前节点,那么左右孩子就可以偷,至于到底偷不偷一定是选一个最大的,所以:val2 = max(left[0], left[1]) + max(right[0], right[1]);
最后当前节点的状态就是{val2, val1}; 即:{不偷当前节点得到的最大金钱,偷当前节点得到的最大金钱}
3. 确定遍历顺序
对二叉树使用后序遍历,这样可以先处理左右节点,然后在对中节点进行处理。
5. 实现
递归的思路乍一看比较绕,但实际上单步的逻辑是非常清晰明了的。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rob(self, root: Optional[TreeNode]) -> int:
dp = self.traversal(root)
return max(dp)
def traversal(self, cur_node):
if not cur_node:
return (0, 0)
left = self.traversal(cur_node.left)
right = self.traversal(cur_node.right)
## 后序遍历 处理偷和不偷两种情况
# 不偷当前节点 子节点也可能是被跳过的
val_0 = max(left[0], left[1]) + max(right[0], right[1])
# 偷当前节点
val_1 = cur_node.val + left[0] + right[0]
return (val_0, val_1)买卖股票系列
121. 买卖股票的最佳时机
0. 买卖股票1:只允许一次买卖
可以使用暴力搜索(嵌套循环);贪心(右侧最大 - 左侧最小)都可以解决
class Solution:
def maxProfit(self, prices: List[int]) -> int:
low = float("inf")
result = 0
for i in range(len(prices)):
low = min(low, prices[i]) #取最左最小价格
result = max(result, prices[i] - low) #直接取最大区间利润
return result1. dp数组以及下标的含义
一个shape = [n, 2] 的 dp数组。dp[i][0] 表示第i天买入股票所得最多现金,dp[i][1] 表示第i天卖出股票所得最多现金。
2. 状态转移方程
如果第i天持有股票即dp[i][0], 那么可以由两个状态推出来
第i-1天就持有股票,那么就保持现状,所得现金就是昨天持有股票的所得现金 即:dp[i - 1][0]
第i天买入股票,所得现金就是买入今天的股票后所得现金即:-prices[i]
dp[i][0] = max(dp[i - 1][0], -prices[i])如果第i天不持有股票即dp[i][1], 也可以由两个状态推出来
第i-1天就不持有股票,那么就保持现状,所得现金就是昨天不持有股票的所得现金 即:dp[i - 1][1]
第i天卖出股票,所得现金就是按照今天股票价格卖出后所得现金即:prices[i] + dp[i - 1][0]
同样dp[i][1]取最大的:
dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0])这里就和上一题呼应上了,通过遍历每一天里的持有和不持有状态,来计算最大收益。dp[i][0]的状态转移规则可以检查在最低点买入的机会(相反数取最大值),dp[i][1]则依赖这个基础来求最大收益值。
3. dp数组初始化
之所以设置 dp[i][0] 第i天持有股票所得最多现金,是因为当选择持有时,现金数额应该减去花费。 所以dp[0][0] 应该初始化成第一天股票价格负数。
4. 确定遍历顺序
顺序遍历天数即可
5. 实现
class Solution:
def maxProfit(self, prices: List[int]) -> int:
dp = [[0] * 2 for _ in range(len(prices))]
dp[0][0] = -prices[0]
for i in range(1, len(prices)):
dp[i][0] = max(dp[i - 1][0], -prices[i])
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i])
return dp[len(prices) - 1][1]122. 买卖股票的最佳时机 II
0. 买卖股票2:允许多次的买卖
贪心仍然可以解决,因为处理的是单调问题。简单思路就是,今天有得赚,明天赚的少了,就赶紧卖出,参考代码。
1. dp数组以及下标的含义
一个shape = [n, 2] 的 dp数组。dp[i][0] 表示第i天买入股票所得最多现金,dp[i][1] 表示第i天卖出股票所得最多现金。
2. 状态转移方程
由于本题中多了中途卖出的过程,这会影响到 dp[i][0] 位的判断。
也就是说,昨天卖出股票手上的余额 减去 今天的股价,如果大于不卖出一直持有的余额,说明昨天的交易会挣钱,那么今天就要买入。
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i])如果第i天卖出股票即dp[i][1], 也可以由两个状态推出来
第i-1天卖出股票手上的余额,对比今天卖出手中的余额,同样取最大的:
dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0])我们通过维护每一天两个状态下手中的余额,来取使得两个状态下余额都是最大的情况,最后推导出收益。 需要注意:dp[i][1],表示的是第i天,买入股票的状态,并不是说一定要第i天买入股票。
3. dp数组初始化
之所以设置 dp[i][0] 第i天持有股票所得最多现金,是因为当选择持有时,现金数额应该减去花费。 所以dp[0][0] 应该初始化成第一天股票价格负数。
4. 确定遍历顺序
顺序遍历天数即可
5. 实现
class Solution:
def maxProfit(self, prices: List[int]) -> int:
dp = [[0] * 2 for _ in range(len(prices))]
dp[0][0] = -prices[0]
for i in range(1, len(prices)):
## 计算昨天卖出+今天买入 和一直持有的收益
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i])
## 计算昨天卖出和今天卖出的收益
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i])
# print(dp)
return dp[len(prices) - 1][1]123. 买卖股票的最佳时机 III
0. 买卖股票3:最多进行两次买卖,交易不能重合
复杂点在于,至多买卖两次,这意味着可以买卖一次,可以买卖两次,也可以不买卖。
1. dp数组以及下标的含义
由于我们监控的是今天买入或卖出,手中实际的利润,那么这里的每一天中可能有5种状态:
0. 无操作(可以不考虑)
1. 第一次买入
2. 第一次卖出
3. 第二次买入
4. 第二次卖出
dp数组的定义也就清楚了:dp[i][j]中 i表示第i天,j为 [0 - 4] 五个状态,dp[i][j]表示第i天状态j所剩最大现金。
2. 状态转移方程
达到 dp[i][1]状态,有两个具体操作:
操作一:第i天买入股票了,那么dp[i][1] = dp[i-1][0] - prices[i]
操作二:第i天没有操作,而是沿用前一天买入的状态,即:dp[i][1] = dp[i - 1][1]
选择:dp[i-1][0] - prices[i],和 dp[i - 1][1] 中更大的,理由同上一个问题一样,始终确保在任何状态下手上的利润最大化。
同理 dp[i][2]也有两个操作:
操作一:第i天卖出股票了,那么dp[i][2] = dp[i - 1][1] + prices[i]
操作二:第i天没有操作,沿用前一天卖出股票的状态,即:dp[i][2] = dp[i - 1][2]
所以dp[i][2] = max(dp[i - 1][1] + prices[i], dp[i - 1][2])
继续 dp[i][3]也有两个操作:
操作一:第i天第二次买入股票了,那么dp[i][3] = dp[i-1][2] - prices[i] 此时上一支一定卖出了
操作二:第i天没有操作,而是沿用前一天买入的状态,即:dp[i][3] = dp[i - 1][3]
最后 dp[i][4]也有两个操作:
操作一:第i天卖出股票了,那么dp[i][4] = dp[i - 1][3] + prices[i]
操作二:第i天没有操作,沿用前一天卖出股票的状态,即:dp[i][4] = dp[i - 1][4]
所以dp[i][4] = max(dp[i - 1][3] + prices[i], dp[i - 1][4])
3. dp数组初始化
示例四表示如果只有一天,那么即使操作了也是收益0的状态。
因此,我们可以将 dp[0][0] 初始为 0;将 dp[0][1] 初始成 -price[0];dp[0][2] 初始成0;dp[0][3] 同样初始为 -price[0]。相当于一天内全部操作了一遍,符合边界条件。
4. 确定遍历顺序
顺序遍历天数即可
5. 实现 不同状态之间的互相影响
可以发现,这个题目以及上一题都描述了状态之间的互相影响,也是题目的考察点和难点。实际上,下面的代码也可以通过一维dp来解决。
class Solution:
def maxProfit(self, prices: List[int]) -> int:
dp = [[0] * 5 for _ in range(len(prices))]
dp[0][1] = dp[0][3] = -prices[0]
for i in range(1, len(prices)):
dp[i][0] = dp[i - 1][0]
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i])
dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i])
dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i])
dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i])
# print(dp)
return dp[-1][-1]188. 买卖股票的最佳时机 IV
0. 买卖股票3:最多进行k次买卖,交易不能重合
1. dp数组以及下标的含义
参考上题的两次操作:
0. 无操作(可以不考虑)
1. 第一次买入
2. 第一次卖出
3. 第二次买入
4. 第二次卖出
......
2k. 第k次买入
2k + 1. 第k次卖出
dp[i][j]中 i表示第i天,j为 [0: 2k + 1] 个状态,dp[i][j]表示第i天状态j所剩最大现金。
2. 状态转移方程
根据上一题我们已经能够判断每个维度的关联和行为。
首先0维度只做初始化使用,为了简便泛化代码,我们保留这一行
奇数维度全部在记录保持或买入的状态
偶数维度全部在记录保持或卖出的状态
我们将原有的i天降维成一维,但是在输入中添加k次交易。2次交易实际状态维度是5维,因此k次交易的状态维度就是2k + 1维
3. dp数组初始化
示例四表示如果只有一天,那么即使操作了也是收益0的状态。
将 dp[0][奇数列] 初始成 -price[0]
4. 确定遍历顺序
顺序遍历天数即可
5. 实现
在每一天对k做一次循环,实现泛化
class Solution:
def maxProfit(self, k: int, prices: List[int]) -> int:
n = 2 * k + 1
dp = [0] * n
for i in range(n):
if i % 2 != 0:
dp[i] = -prices[0]
for i in range(1, len(prices)):
for j in range(n):
if j == 0:
continue
elif j % 2 != 0:
dp[j] = max(dp[j], dp[j - 1] - prices[i])
elif j % 2 == 0:
dp[j] = max(dp[j], dp[j - 1] + prices[i])
# print(dp)
return dp[-1]309. 买卖股票的最佳时机含冷冻期
0. 买卖股票冷冻期:卖出的第二天不能购买股票
已经熟悉了持有和售出这类不同状态对于dp影响的案例,这里添加了冷冻期限制,但购买次数不限
1. dp数组以及下标的含义
一个shape = [n, 2] 的 dp数组。dp[i][0] 表示第i天买入股票所得最多现金,dp[i][1] 表示第i天卖出股票所得最多现金。
2. 状态转移方程
多了 中途卖出+冷冻期 的过程,这会影响状态判断。
和上面一样,不要考虑哪一天买入卖出,只考虑状态,我们列举一下每一天可能的情况:
1. 持有状态;2. 卖出状态(已经度过冷冻期但不持有);3. 卖出状态(卖出当天);4. 卖出状态(冷冻期内)。
这里度过冷冻期但不持有,最好和冷冻期内区分对待,这是为了方便后续的状态转移分析。
现在来看每个状态之间的互相影响:
第一个,i天是持有状态可能的来源:
1. 前一天就持有 dp[i][0] = dp[i - 1][0];
2. 前一天是冷冻期,今天买入 dp[i][0] = dp[i - 1][3] - price[i]
3. 前一天不是冷冻期,但一直不持有,今天买入 dp[i][0] = dp[i - 1][1] - price[i]
这里有一个坑点,需要先比较2和3谁的值更大,用更大的值减价格
dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3] - prices[i], dp[i - 1][1]) - prices[i])第二个,卖出状态(已经度过冷冻期但不持有):
1. 前一天是卖出,不处于冷冻期内 dp[i][1] = dp[i - 1][0]
2. 前一天就是卖出,处于冷冻期内 dp[i][1] = dp[i - 1][3]
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3])第三个, 卖出状态(卖出当天):
前一天肯定是持有的
dp[i][2] = dp[i - 1][0] + prices[i]第四个, 卖出状态(冷冻期内):
前一天肯定刚卖出
dp[i][3] = dp[i - 1][2]3. dp数组初始化
对第一天进行持有的初始化,其他位置全0即可
4. 确定遍历顺序
顺序遍历天数即可
5. 实现
class Solution:
def maxProfit(self, prices: List[int]) -> int:
dp = [[0] * 4 for _ in range(len(prices))]
dp[0][0] = -prices[0]
print(dp)
for i in range(1, len(prices)):
dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3], dp[i - 1][1]) - prices[i])
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3])
dp[i][2] = dp[i - 1][0] + prices[i]
dp[i][3] = dp[i - 1][2]
# print(dp)
return max(dp[-1][3], dp[-1][1], dp[-1][2])714. 买卖股票的最佳时机含手续费
0. 买卖股票带手续费:多次交易,卖出扣费
状态转移方程
持有状态不受手续费影响,一种是前一天就持有,另一种是今天持有。
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i])如果第i天卖出股票即dp[i][1], 也可以由两个状态推出来
第i-1天卖出股票手上的余额,对比今天卖出手中的余额 扣除手续费,取最大的:
dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0])实现:
class Solution:
def maxProfit(self, prices: List[int], fee: int) -> int:
n =len(prices)
dp = [[0] * 2 for _ in range(n)]
dp[0][0] = -prices[0]
for i in range(1, n):
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i])
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee)
# print(dp)
return dp[-1][-1]