ps: 滴滴滴~上班打卡…
一、实验目的
熟练掌握二叉树的二叉链表存储结构的C语言实现。掌握二叉树的基本操作前序、中序、后序遍历二叉树的三种方法。了解非递归遍历过程中“栈”的作用和状态,而且能灵活运用遍历算法实现二叉树的其它操作。
二、实验内容
(1) 二叉树的二叉链表的创建。
(2) 二叉树的前、中、后序遍历的递归算法和非递归算法的实现
(3) 求二叉树中叶子结点数目的递归算法。(本报告未选做)
(4) 编写求二叉树深度的递归算法。 (选做)
(5) 编写判断二叉树是否相似的递归算法。 (本报告未选做)
(6) 编写求二叉树左右子树互换的递归算法。 (本报告未选做)
(7) 编写二叉树层序遍历的算法。 (本报告未选做)
(8) 编写判断二叉树是否是完全二叉树的算法。(本报告未选做)
创建二叉树的二叉链表结构、进行先、中、后序的递归函数显示不同遍历序列,结合习题了解二叉树遍历的应用实例。
编写前、中、后、层序遍历的非遍历函数,注意用以前做过的栈和队列作辅助存储结构。掌握用遍历算法求解其它问题的方法。
三、问题描述
题目概况:深度优先遍历和广度优先遍历(含非递归);求二叉树深度的递归算法(选做)。
四、数据结构定义
栈的链式存储、队列的顺序存储,数据元素整型。
五、算法思想及算法设计
二叉树的遍历分为两类,一类是深度优先遍历,一类是广度优先遍历。
5.1 深度优先遍历
二叉树的深度优先遍历有三种方式,先序、中序和后序遍历,三种遍历的不同在于访问根节点的顺序。由于二叉树本身在创建时运用递归,其含义也包含递归意义,所以用递归思想去遍历二叉树很容易理解而且代码简洁,下面介绍三种遍历的递归算法。
5.1.1 先序遍历递归算法
若二叉树为空,则空操作;
否则:
<1> 访问根节点
<2> 先序遍历左子树
<3> 先序遍历右子树
代码如下:
void PreOrder(Treenode T)
{
if (T == NULL)
return;
printf("%d ", T->data); // 访问根节点(可另写visit函数,下同)
PreOrder(T->lchild); // 先序遍历左子树
PreOrder(T->rchild); // 先序遍历右子树
return;
}
5.1.2 中序遍历递归算法
若二叉树为空,则空操作;
否则:
<1> 中序遍历左子树
<2> 访问根节点
<3> 中序遍历右子树
代码如下:
void InOrder(Treenode T)
{
if (T == NULL)
return;
InOrder(T->lchild); // 中序遍历左子树
printf("%d ", T->data); // 访问根节点
InOrder(T->rchild); // 中序遍历右子树
return;
}
5.1.3 后序遍历递归算法
若二叉树为空,则空操作;
否则:
<1> 后序遍历左子树
<2> 后序遍历右子树
<3> 访问根节点
代码如下:
void PostOrder(Treenode T)
{
if (T == NULL)
return;
PostOrder(T->lchild); // 后序遍历左子树
PostOrder(T->rchild); // 后序遍历右子树
printf("%d ", T->data); // 访问根节点
return;
}
以上三种递归遍历只有访问根节点先后不同,对于左右子树均是调用本函数递归完 成,每个节点访问一次,时间复杂度为 O(n),n为节点数。
而对于下面三种遍历方式的非递归算法,则需要用到栈的思想去实现。
5.1.4 先序遍历非递归算法
思考:先序遍历先访问根节点,然后转向左子树,对左子树也是前述操作,当NULL时,便要开始转向右子树,对右子树也是上述操作。
--------不难想到,对于已经访问过的节点,在转向右子树时仍然需要调用(因为你想转到右子树就要知晓是哪个节点的右子树,而这个节点已经访问过了,具体操作见“六、运行示例”),那么这些访问过的节点便需要储存起来,方便后续调用。
--------由于是从最左下方的节点逐渐往回调用,那么栈“后进先出”的思想便可以应用在这里。
代码如下:
void PreOrderTraverse(Treenode root)
{
lstack S;
InitLinkStack(S);
Treenode p = (Treenode)malloc(sizeof(Tree));
p = root;
while (p != NULL || !judgeNULL(S))
{
while (p != NULL)//p 从根节点一直往左滑,访问完便放进栈中;
//直到最左下方 p 为空停止,p 为空就是它双亲节点左子树为空;
{
visit(p->data);
Push(S, p);
p = p->lchild;
}
//而且双亲本身已经被访问过;
//那么接下来该访问其右子树
if (!judgeNULL(S))
{
Pop(S, p);//出栈,给 p 赋值
p = p->rchild;//转向右子树,然后再回到上边 while 循环
}
}//重复以上过程
}
5.1.5 中序遍历非递归算法
思考:中序遍历先访问左子树,再访问根节点,最后访问右子树。在左右子树中也是上述过程。所以相比于先序遍历,中序遍历压入栈内的节点应是还未被访问的根节点,栈里面每个节点还要涉及节点自身的访问以及遍历其右子树过程。
代码如下:
void InOrderTraverse(Treenode root)
{
lstack s;
InitLinkStack(s);
Treenode p = (Treenode)malloc(sizeof(Tree));
p = root;
while (p != NULL || !JudgeNULL(s))
{
if (p)//p!=NULL 的就要进栈等待
{
Push(s, p);
p = p->lchild;
}
else//p==NULL 时,说明 p 指向了“最左”下方节点的左孩子(此左孩子空)
{
Pop(s, p);
visit(p->data);//此根节点作为双亲而被输出(根节点访问)
p = p->rchild;//转向此根节点的右子树,重复上述过程。
}
}
}
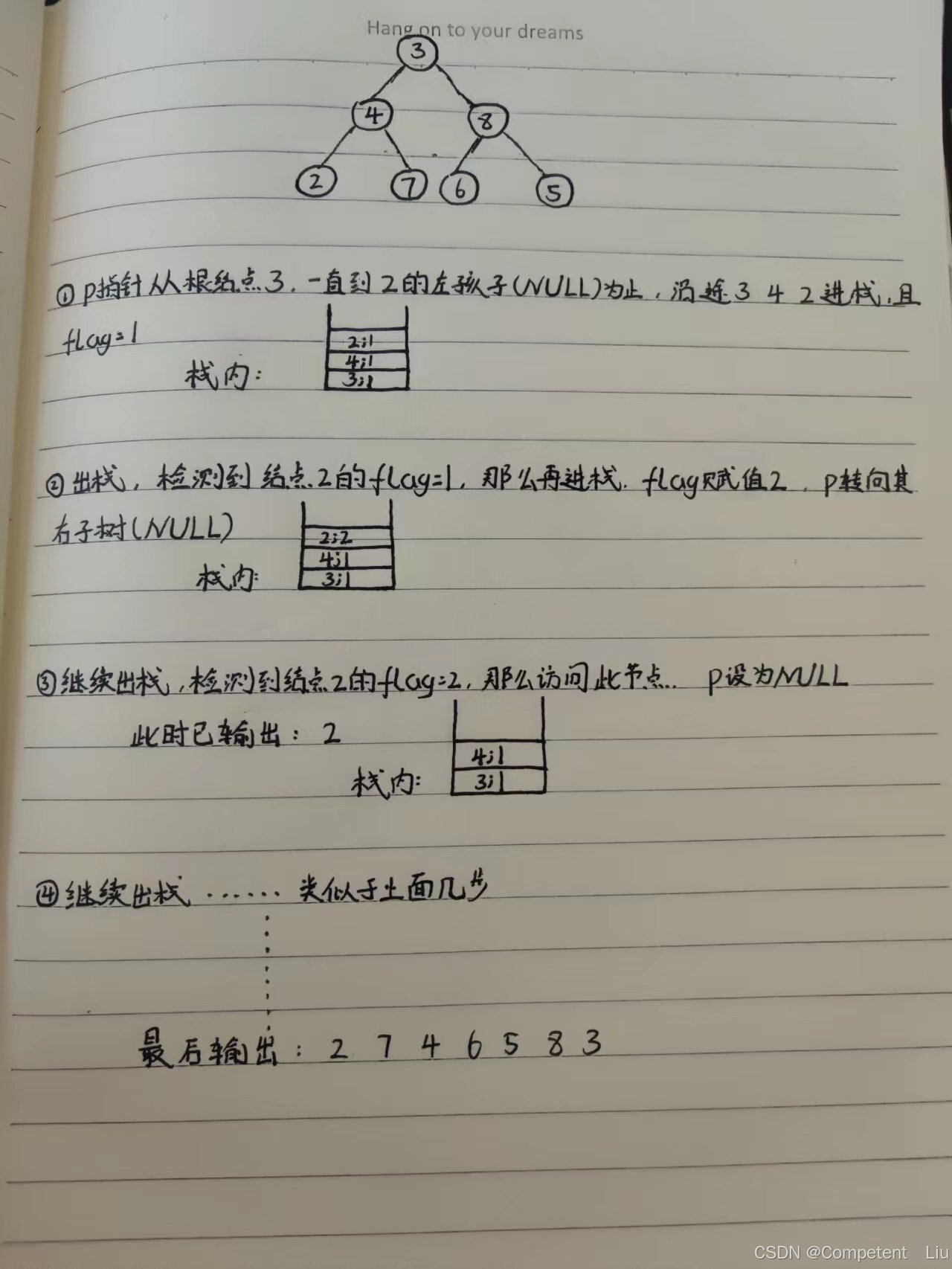
5.1.6 后序遍历非递归算法
思考:
后序遍历先访问左子树,再访问右子树,最后访问根节点。中序遍历也是先访问左子树-------->
由此不难设想到后序遍历也应该是像中序遍历那样根节点一一进栈,访问完左子树之后出栈。
和中序遍历不同的是,这里出栈的节点不能被访问,而是先要去遍历右子树。那么这个节点就又要被储存起来以待最后的访问,等右子树遍历完之后,再出栈再被访问。
所以一个节点应有两次进出栈过程,所以表示节点的结构体中应另设 flag,表示进栈次数。
代码如下:
void postOrderTraverse(Treenode root)
{
lstack S;
ELEM elem;
InitLinkStack(S);
Treenode p = (Treenode)malloc(sizeof(Tree));
p = root;
while (p != NULL || !judgeNULL(S))
{
if (p != NULL)//访问左子树
{
elem = (ELEM)malloc(sizeof(Elem));
elem->ptr = (Treenode)malloc(sizeof(Tree));
elem->ptr = p;
elem->flag = 1;//flag 赋值 1,表示第一次进栈
Push(S, elem);
p = p->lchild;//继续向左
}
else
{
Pop(S, elem);//出栈
p = elem->ptr;
if (elem->flag == 1)//flag=1 说明只访问过左子树,还需要处理其右子树
{
elem->flag = 2;//flag 赋值 2,表示第二次进栈
Push(S, elem);
p = p->rchild;//转向右子树
}
else//flag=2 说明左右子树均已访问
{
visit(p->data);//访问此节点
p = NULL;//设为空,继续出栈
}
}
}
}
对于非递归的三种算法,其本质的不同是访问根节点的顺序不同,每个节点都要进出栈还要访问的操作没有改变,所以对于n个节点的二叉树,三种非递归算法时间复杂度均为 O(n).
注:以上六种算法的完整代码请见“七、实验代码”部分
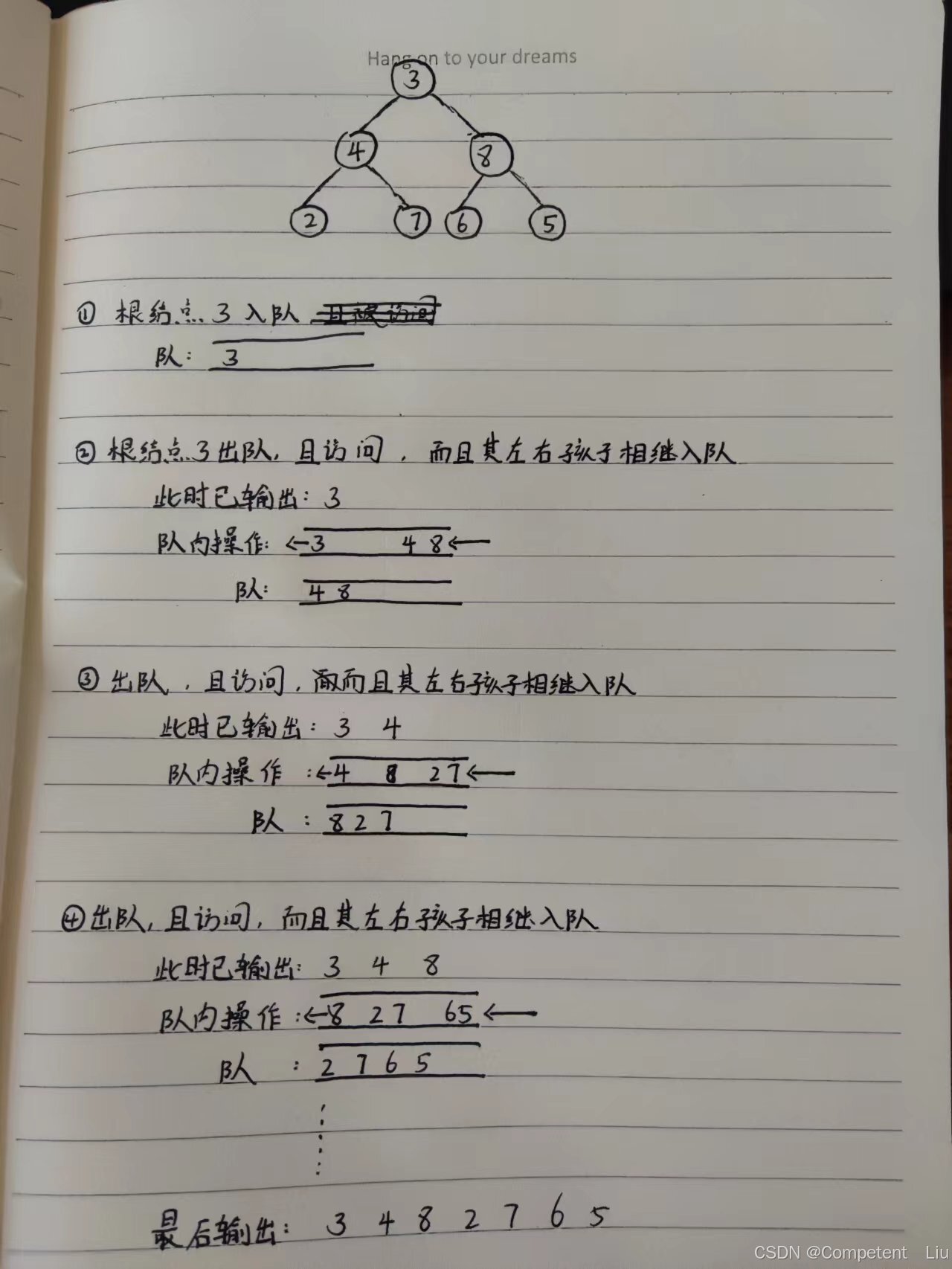
5.2 广度优先遍历
思考:层序遍历从上到下,每一层从做往右一一访问。
层与层之间有着双亲与孩子的联系,通过指针可以做到逐层从上到下,
亟待解决的问题是每一层的从左往右,也就是先左孩子后右孩子的问题。
而这一层的左孩子和右孩子又是下一层左右孩子的双亲,对于这下一层而言也要从左往右访问。所以这种“从左往右”访问的顺序有“继承”关系,上一层的从左往右继承到下一层…队列“先进先出”思想便可以应用在这里。
代码如下:
void LevelOrder(Tree T, Queue Q)
{
Tree temp;
Push(&Q, T); // 根节点入队
while (TreeSize > 0) {
temp = Pop(&Q); // 出队
TreeSize--;
printf("%d ", temp->data); // 访问
if (temp->lchild) // 如果此出队节点有左孩子,那么入队
Push(&Q, temp->lchild);
if (temp->rchild) // 如果此出队节点有右孩子,那么入队
Push(&Q, temp->rchild);
// 这里两个 if 先后不能颠倒,体现了顺序的“继承”关系
}
}
5.3 (选做)实验内容(4)
题目:编写求二叉树深度的递归算法。
思考:递归算法一般都是嵌套调用本身,然后逐渐 return返回到表层达到一个目的。对于二叉树的深度,可以通过一层层的节点深入到最后一层叶子结点,然后return返回到最初的根节点,期间需要一个变量来统计返回次数,达到求深度的目的。
代码如下:
Status depth(Treenode T)
{
if (T == NULL)
return 0;
else
{
m = depth(T->lchild); // 因为不是完全二叉树,所以左右子树深度要分别统计
n = depth(T->rchild);
if (m > n)
return m + 1; // 哪个深度大,就再加一,作为整棵树的深度
else
return n + 1;
}
}
六、运行示例
6.1 先序遍历非递归图示
6.2 中序遍历非递归图示
6.3 后序遍历非递归
6.3 层序遍历
七、实验代码
7.1 前、中、后序递归算法
//FileName:code5.1.cpp
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
typedef int Status;
typedef struct tree
{
int data;
struct tree* lchild;
struct tree* rchild;
}Tree, * Treenode;
Treenode CreatTree()
{
Treenode T;
int data;
scanf("%d", &data);
if (data == -1)return NULL;
else
{
T = (Treenode)malloc(sizeof(Tree));
if (T)
{
T->data = data;
printf("Please input %d's lchild: ", data);
T->lchild = CreatTree();
printf("Please input %d's rchild: ", data);
T->rchild = CreatTree();
return T;
}
}
}
void PreOrder(Treenode T)
{
if (T == NULL)return;
printf("%d ", T->data);
PreOrder(T->lchild);
PreOrder(T->rchild);
return;
}
void InOrder(Treenode T)
{
if (T == NULL)return;
InOrder(T->lchild);
printf("%d ", T->data);
InOrder(T->rchild);
return;
}
void PostOrder(Treenode T)
{
if (T == NULL)return;
PostOrder(T->lchild);
PostOrder(T->rchild);
printf("%d ", T->data);
return;
}
int main()
{
Treenode T;
printf("Please input root's data: ");
T = CreatTree();
printf("\n前序遍历为:");
PreOrder(T);
printf("\n中序遍历为:");
InOrder(T);
printf("\n后序遍历为:");
PostOrder(T);
}
7.2 先序遍历非递归(完整代码)
//FileName:PreOrderTraverse.cpp
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#define ERROR 0
#define OK 1
typedef int Status;
typedef struct tree
{
int data;
struct tree* lchild;
struct tree* rchild;
}Tree, * Treenode;
typedef struct stack
{
Treenode node;
struct stack* next;
}Stack, * lstack;
void InitLinkStack(lstack& L)
{
L = (lstack)malloc(sizeof(Stack));
if (!L)
{
printf("ERROR!"); return;
}
L->node = NULL;
L->next = NULL;
}
Status Push(lstack& L, Treenode e)
{
lstack Newnode;
Newnode = (lstack)malloc(sizeof(Stack));
if (!Newnode)
{
printf("Building Newnode has failed!"); return 0;
}
Newnode->node = e;
Newnode->next = L;
L = Newnode;
return OK;
}
Status Pop(lstack& L, Treenode& e)
{
if (!L)
{
printf("Stack has been empty!"); return 0;
}
lstack p = L;
e = p->node;
L = L->next;
free(p);
p = NULL;
return OK;
}
Status judgeNULL(lstack L)
{
if (L == NULL)
{
return OK;
}
else
{
return ERROR;
}
}
void visit(int x)
{
printf("%d ", x);
}
Treenode CreatTree()
{
int data;
Treenode S;
scanf("%d", &data);
if (data == -1)return NULL;
else
{
S = (Treenode)malloc(sizeof(Tree));
if (S)
{
S->data = data;
printf("Please input lchild of %d: ", data);
S->lchild = CreatTree();
printf("Please input rchild of %d: ", data);
S->rchild = CreatTree();
return S;
}
}
}
void PreOrderTraverse(Treenode root)
{
lstack S;
InitLinkStack(S);
Treenode p = (Treenode)malloc(sizeof(Tree));
p = root;
while (p != NULL || !judgeNULL(S))
{
while (p != NULL)
{
visit(p->data);
Push(S, p);
p = p->lchild;
}
if (!judgeNULL(S))
{
Pop(S, p);
p = p->rchild;
}
}
}
int main()
{
Treenode T;
printf("Please input root's data: ");
T = CreatTree();
PreOrderTraverse(T);
return 0;
}
7.3 中序遍历非递归(完整代码)
//FileName:InOrderTraverse.cpp
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
typedef int Status;
#define OK 1
#define ERROR 0
typedef struct tree
{
int data;
struct tree* lchild;
struct tree* rchild;
}Tree, * Treenode;
typedef struct stack
{
Treenode node;
struct stack* next;
}Stack, * lstack;
void InitLinkStack(lstack& s)
{
s = (lstack)malloc(sizeof(Stack));
if (!s)return;
s->next = NULL;
s->node = NULL;
}
Status Push(lstack& s, Treenode e)
{
lstack Newnode;
Newnode = (lstack)malloc(sizeof(Stack));
if (!Newnode)return ERROR;
Newnode->node = e;
Newnode->next = s;
s = Newnode;
return OK;
}
Status Pop(lstack& s, Treenode& e)
{
if (!s)return ERROR;
lstack p = s;
e = p->node;
s = s->next;
free(p);
p = NULL;
return OK;
}
Status JudgeNULL(lstack s)
{
if (s == NULL)return OK;
else return ERROR;
}
void visit(int x)
{
printf("%d ", x);
return;
}
Treenode CreatTree()
{
Treenode T;
int data;
scanf("%d", &data);
if (data == -1)return NULL;
else
{
T = (Treenode)malloc(sizeof(Tree));
if (T)
{
T->data = data;
printf("Please input lchild of %d: ", data);
T->lchild = CreatTree();
printf("Please input rchild of %d: ", data);
T->rchild = CreatTree();
return T;
}
}
}
void InOrderTraverse(Treenode root)
{
lstack s;
InitLinkStack(s);
Treenode p = (Treenode)malloc(sizeof(Tree));
p = root;
while (p != NULL || !JudgeNULL(s))
{
if (p)
{
Push(s, p);
p = p->lchild;
}
else
{
Pop(s, p);
visit(p->data);
p = p->rchild;
}
}
}
int main()
{
Treenode T;
printf("Please input root's data: ");
T = CreatTree();
InOrderTraverse(T);
return 0;
}
7.4 后序遍历非递归(完整代码)
//FileName:PostOrderTraverse.cpp
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#define ERROR 0
#define OK 1
typedef int Status;
typedef struct tree
{
int data;
struct tree* lchild;
struct tree* rchild;
}Tree, * Treenode;
typedef struct Element
{
Treenode ptr;
int flag;
}Elem, * ELEM;
typedef struct stack
{
ELEM node;
struct stack* next;
}Stack, * lstack;
void InitLinkStack(lstack& L)
{
L = (lstack)malloc(sizeof(Stack));
if (!L)
{
printf("ERROR!"); return;
}
L->node = NULL;
L->next = NULL;
}
Status Push(lstack& L, ELEM e)
{
lstack Newnode;
Newnode = (lstack)malloc(sizeof(Stack));
if (!Newnode)
{
printf("Building Newnode has failed!"); return ERROR;
}
Newnode->node = e;
Newnode->next = L->next;
L->next = Newnode;
return OK;
}
Status Pop(lstack& L, ELEM& e)
{
if (!L->next)
{
printf("Stack has been empty!"); return ERROR;
}
lstack p = L->next;
e = p->node;
L->next = p->next;
free(p);
p = NULL;
return OK;
}
Status judgeNULL(lstack L)
{
if (L->next == NULL)
{
return OK;
}
else
{
return ERROR;
}
}
void visit(int x)
{
printf("%d ", x);
}
Treenode CreatTree()
{
int data;
ELEM S;
scanf("%d", &data);
if (data == -1)return NULL;
else
{
S = (ELEM)malloc(sizeof(Elem));
S->ptr = (Treenode)malloc(sizeof(Tree));
if (S && S->ptr)
{
S->ptr->data = data;
printf("Please input lchild of %d: ", data);
S->ptr->lchild = CreatTree();
printf("Please input rchild of %d: ", data);
S->ptr->rchild = CreatTree();
return S->ptr;
}
}
}
void postOrderTraverse(Treenode root)
{
lstack S;
ELEM elem;
InitLinkStack(S);
Treenode p = (Treenode)malloc(sizeof(Tree));
p = root;
while (p != NULL || !judgeNULL(S))
{
if (p != NULL)
{
elem = (ELEM)malloc(sizeof(Elem));
elem->ptr = (Treenode)malloc(sizeof(Tree));
elem->ptr = p;
elem->flag = 1;
Push(S, elem);
p = p->lchild;
}
else
{
Pop(S, elem);
p = elem->ptr;
if (elem->flag == 1)
{
elem->flag = 2;
Push(S, elem);
p = p->rchild;
}
else
{
visit(p->data);
p = NULL;
}
}
}
}
int main()
{
Treenode T;
printf("Please input root's data: ");
T = CreatTree();
postOrderTraverse(T);
return 0;
}
7.5 层序遍历(完整代码)
//FileName:LevelOrderTraverse.cpp
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include <stdlib.h>
#define MAXSIZE 100
typedef struct Node
{
int data;
struct Node* rchild, * lchild;
}Node, * Tree;
int TreeSize = 0;
typedef struct Queue
{
struct Node* num[MAXSIZE];
int front;
int rear;
}Queue;
void Init(Queue& Q)
{
Q.front = 0;
Q.rear = 0;
}
void Push(Queue* Q, Node* e)
{
Q->num[++Q->rear] = e;
}
Node* Pop(Queue* Q)
{
return Q->num[++Q->front];
}
void Create(Tree& T)
{
int e;
scanf("%d", &e);
if (e == -1)
return;
else {
TreeSize++;
T = (Tree)malloc(sizeof(Node));
T->data = e;
printf("Please input lchild of %d: ", T->data);
Create(T->lchild);
printf("Please input rchild of %d: ", T->data);
Create(T->rchild);
}
}
void LevelOrder(Tree T, Queue Q)
{
Tree temp;
Push(&Q, T);
while (TreeSize > 0) {
temp = Pop(&Q);
TreeSize--;
printf("%d ", temp->data);
if (temp->lchild)
Push(&Q, temp->lchild);
if (temp->rchild)
Push(&Q, temp->rchild);
}
}
int main()
{
Queue Q;
Init(Q);
Tree T;
printf("Please input root's data: ");
Create(T);
LevelOrder(T, Q);
return 0;
}
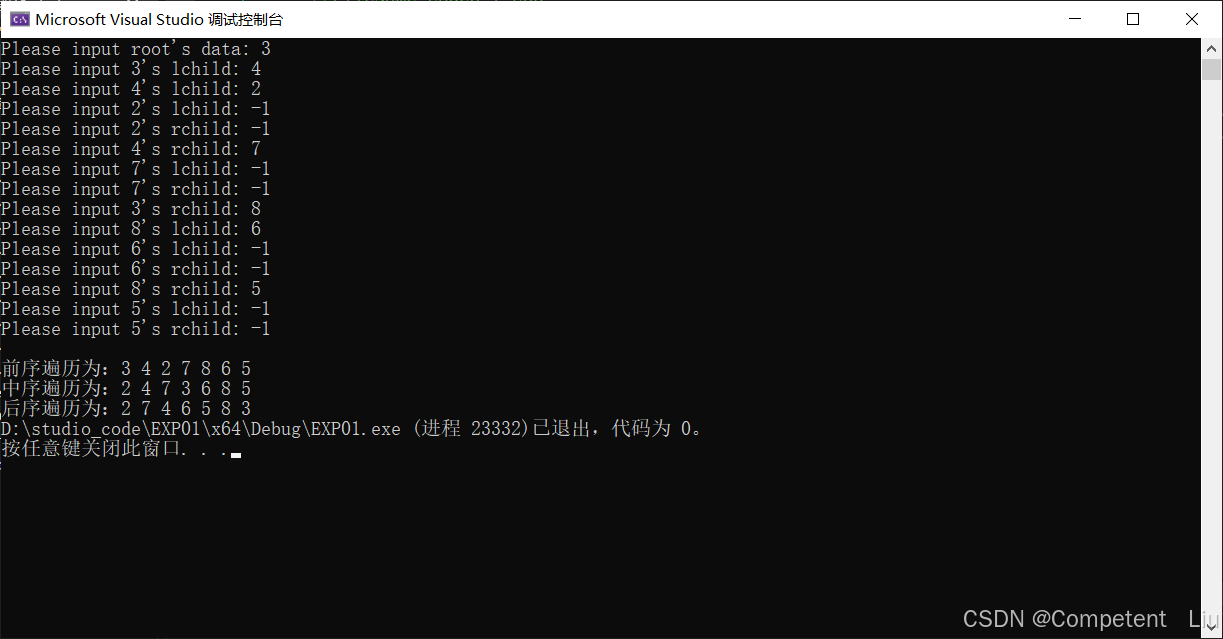
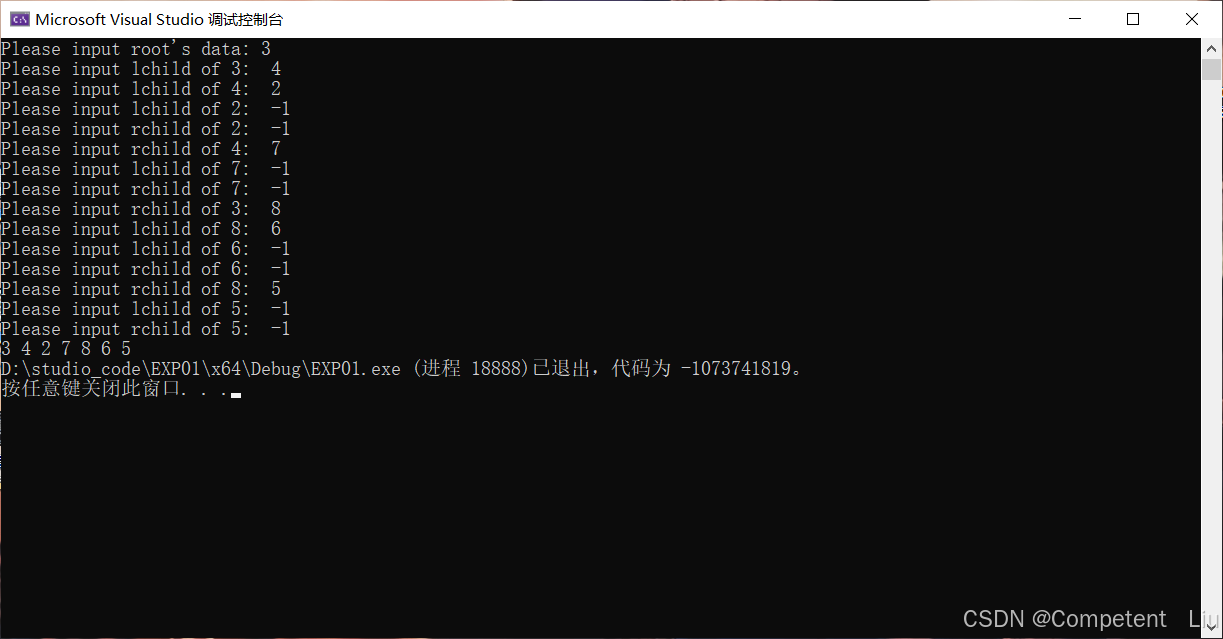
八、算法测试结果
测试结果在“七、实验代码”部分已给出,输入完全相同,均为“六、运行示例”部分的图中所示二叉树。
九、分析与总结
9.1 算法复杂度分析及优、缺点分析
- 算法时间复杂度均为 O(n)。
- 三个非递归算法均利用栈思想辅助操作,结构清晰易懂。
- 层序遍历利用队列思想辅助操作,使得代码简洁易懂,但是只有固定的储存空间,超出规定的队列长度会引起报错。
9.2 实验总结
- 对于遍历二叉树的各种方法进行了练习,更好的理解了二叉树的结构意义。
- 对于递归算法,代码简洁易懂;而非递归算法虽然繁冗,在时间复杂度上也没有优势,但是它利用栈的思想去解决二叉树的三种遍历方式值得深入探讨研究,在解决其他二叉树问题上给到了提示。
- 对于广度优先遍历,利用队列思想层层输出,没有回溯操作,没有出入栈操作, 在运行速度上略高于深度优先遍历;但是广度优先遍历保留了全部节点,所占空间较大。
- 对于深度优先遍历,未保留全部节点,占用空间少;但是有出入栈操作,运行较慢。
ps:这实验好长啊,当时我是咋敲的,累die了…