问题的起源
学习一个知识模块,一般先要厘清学习的目的,一个技术分支的出现必然是应对某个具体问题而产生的解决方案,搞清楚了问题的起源,对解决问题的思路就有了根本性的理解,来龙去脉把握清楚了学习起来就既有动力又有目标了。
回归到红黑树的问题,红黑树其实也是一种平衡树,之前学习过的 AVL 树也是一种平衡树,AVL 的特点是对所谓的“平衡性”要求太严格,或者说太古板,它要求任意一棵子树的左右子树高度差都必须小于等于1,这固然有它的好处,这样做会使得任意时刻树都是最平衡的,所付出的代价是所需要做的移动、旋转的操作比较多。
如果折中去思考,自然会产生这么一个想法:是否可以不那么追求极致平衡?而在节点的操作频次和平衡性之间权衡,牺牲一点平衡性,换取操作性能的提升?
平衡性思考
答案是肯定的,实际应用中的自平衡搜索二叉树,除了 AVL 之外,红黑树是另一位备受宠爱的明星,他不仅是Linux中非线性数据结构的标准算法,在内核中被大量使用,而且是JAVA中TreeMap、TreeSet机制、C++中的STL这些经典工具背后的强大逻辑支撑,也是众多数据库中核心的内置算法结构。
与AVL不同,红黑树并不追求“绝对的平衡”,在毫无平衡性的BST和绝对平衡的AVL之间,红黑树聪明地做了折中,他的左右子树的高度差可以大于1,但任何一棵子树的高度不会大于另一棵兄弟子树高度的两倍。
正是红黑树放弃了AVL的绝对平衡的苛刻要求,获得了更加完美的性能表现。
红黑树的定义
既然不想要像 AVL 树那样的极致平衡,那么我们首先要寻求的是一种“不那么平衡”的平衡树,比如:假设一棵树中,其最长路径比最短路径长2倍以内,我们就认为是平衡的,按照这种标准构建的二叉树肯定不会像 AVL 那么严格。接下来我们还需要更具体的设计,来使得它满足以上所述的特性。
比如,可以这么设计:
- 约定树中的节点都是有颜色的,要么红色,要么黑色。
- 约定根节点的颜色为黑色。
- 约定红色节点不能相邻,但黑色节点可以相邻。
- 约定从任意一个节点开始到叶子的路径包含的黑色节点的个数相等。
如果一棵二叉树满足以上条件,就会使得他不可能有出现:一条路径的长度是另一条路径的两倍以上,这个结论只需看一下4和5两点限制就明白了:最长的路径就是红黑相间的路径,最短的路径就是全黑的路径,由于任何路径的黑色节点数必须相等,因此最长的路径长度最多是最短路径的2倍。这样的约定,比任何子树高度差不大于1要宽松多了,所以红黑树是一种“大致”平衡的二叉树,虽然逻辑比 AVL 复杂不少,但同时带来了操作性能上的提升。
红黑树
红黑树的代码设计
节点设计
为了能够更方便地实现红黑树中的各个限制条件的检测和姿态的调整,需要重新定义树的节点成员如下:
typedef struct node
{
tn_datatype data;
struct node *lchild;
struct node *rchild;
struct node *parent; // 指向父节点的指针
struct node *uncle; // 指向叔节点的指针
int color; // 节点的颜色
}treenode, *linktree;
对比AVL的节点设计,在红黑树中我们增加了树的父节点指针parent和叔节点uncle,以及关键的颜色成员color。下面来讨论一下红黑树是如何保持其“最长路径不会比最短路径长2倍”的特性。
接下来,无非就是讨论插入和删除节点的时候,如何根据红黑树的定义调整节点,使之保持红黑树所约定的约束条件。
插入操作
首先是插入操作,红黑树本质上就是一棵BST,其插入算法实则是一个在利用BST算法插入一个节点之后,再根据节点颜色不断调整的过程。为了方便设计算法,一般将一个新产生的节点的颜色设置为红色,插入之后再做调整。也就是说,插入的步骤是这样的:
- 新创建一个节点,并着色为RED。
- 若树为空,则将此新节点的颜色翻转为BLACK并设置其为根。否则进入第3步。
- 按照BST算法插入新节点。
- 检测该新插入节点,若违反了红黑树的任意一条原则,处理之。
为了方便叙述,作如下约定:
- N(New)为新插入的节点
- P(Parent)为N的父节点
- G(Grandparent)为N的祖父节点
- U(Uncle)为N的叔节点
接下来,就可以讨论插入操作时所发生的所有可能的情况:
【1】黑P:此时插入操作不会违反任何红黑树的约束条件,无需调整。
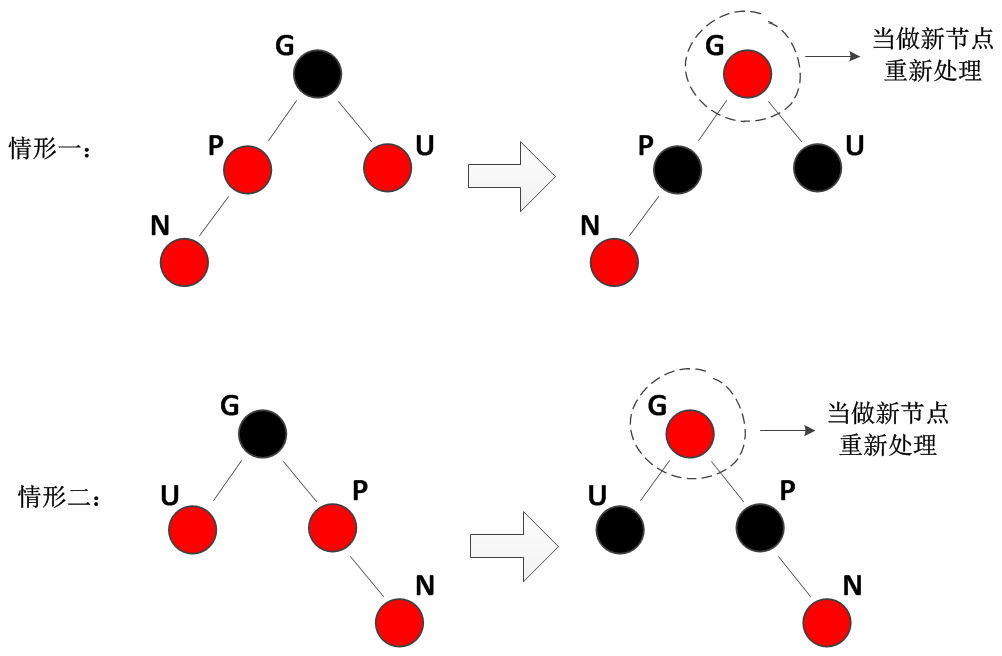
【2】红P红U:此时只需翻转P、U和G的颜色,然后将G当做新节点重新处理即可,如下图所示:
红P红U-插入操作导致不平衡
【3】红P黑U:此时继续拆分为两种对称的情形:
- P是G的左孩子节点。
- P是G的右孩子节点。
由于是对称的,因此只需讨论一种即可,另一种对调左右可得。假设新插入的N节点的父节点P是其祖父节点G的左孩子节点,由于P是红色的,因此违反了红黑树的约束条件,调整的步骤如下:
- 对节点N进行左旋转,假设旋转后P称为N
, N称为P - 翻转G和P`的颜色
- 对节点P`进行右旋转
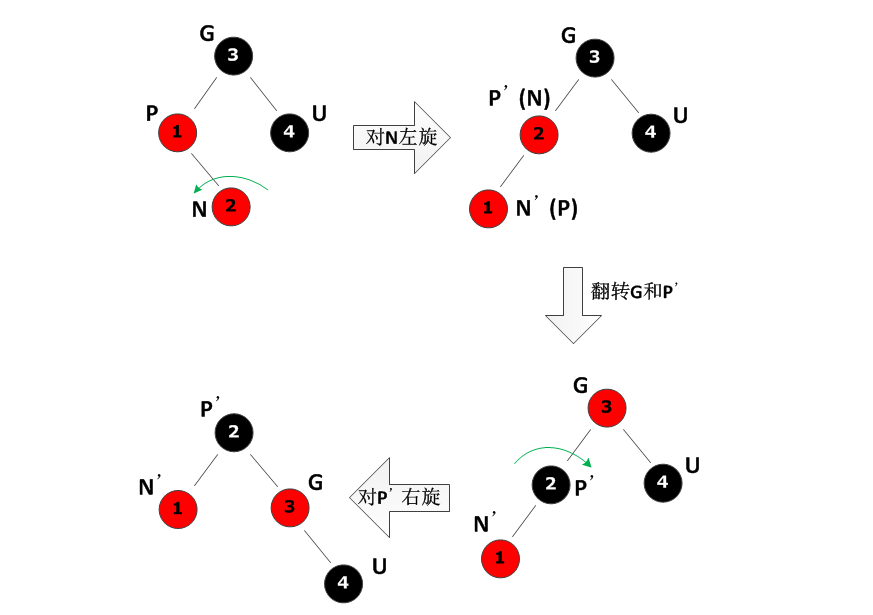
具体过程如下图所示:
红P黑U-插入操作导致不平衡
针对以上所属的情形,可综合给出红黑树的节点插入算法:
void insertFixup(linktree *proot, linktree new)
{
// 1,new为根节点,则直接将其颜色设置为黑
if(new->parent == NULL)
{
new->color = BLACK;
*proot = new;
return;
}
// 2,黑P,不违反任何红黑树平衡约束,无需进一步调整
if(new->parent->color == BLACK)
return;
// 3,红P,需进一步判定
else
insertCase1(proot, new);
}
// 红P红U
void insertCase1(linktree *proot, linktree new)
{
if(uncle(new) != NULL && uncle(new)->color == RED)
{
// 翻转P、U和G的颜色
new->parent->color = BLACK;
uncle(new)->color = BLACK;
grandparent(new)->color = RED;
// 将G当做新节点重新判定其平衡合法性
insertFixup(proot, grandparent(new));
}
else
insertCase2(proot, new);
}
// 红P黑U:G、P、N三个节点不在“一条线”上
void insertCase2(linktree *proot, linktree new)
{
// 新插入的节点new是P的右孩子,且P是G的左孩子
if(new == new->parent->rchild &&
new->parent == grandparent(new)->lchild)
{
rbRotateLeft(proot, new);
new = new->lchild;
}
// 新插入的节点new是P的左孩子,且P是G的右孩子
else if(new == new->parent->lchild &&
new->parent == grandparent(new)->rchild)
{
rbRotateRight(proot, new);
new = new->rchild;
}
// 将G、P、N调整到“一条线”之后,针对原P节点继续调整
insertCase3(proot, new);
}
// 红P黑U:G、P、N三个节点在“一条线”上
void insertCase3(linktree *proot, linktree new)
{
// 翻转G、P颜色
new->parent->color = BLACK;
grandparent(new)->color = RED;
// 对当前P进行旋转
// 保证旋转之后子树各个分支的黑色节点个数保持不变
if(new == new->parent->lchild &&
new->parent == grandparent(new)->lchild)
{
rbRotateRight(proot, new->parent);
}
else
rbRotateLeft(proot, new->parent);
}
// 在一棵红黑树 root 中,插入新节点new
void rbInsert(linktree *proot, linktree new)
{
// 先按 BST 的逻辑插入节点
*proot = bstInsert(*proot, new);
// 然后判定插入节点后是否违反红黑树平衡性约束条件
insertFixup(proot, new);
}
删除操作
删除红黑树节点的原理逻辑
从一棵红黑树中删除一个节点同样要遵循红黑树的所有约束条件,下面将删除节点所能出现的所有情况做一个汇总。
首先明白一点,如果被删除的节点x有两个非空孩子,那么根据BST算法,我们总可以找到左孩子中最大或者右孩子中最小的节点来替代它,这个替代的过程只涉及数据替换,跟节点颜色无关,然后问题就被转化为删除该“最多只有一个孩子”的节点即可。
此时,可将删除节点的情况分成如下几种情形:
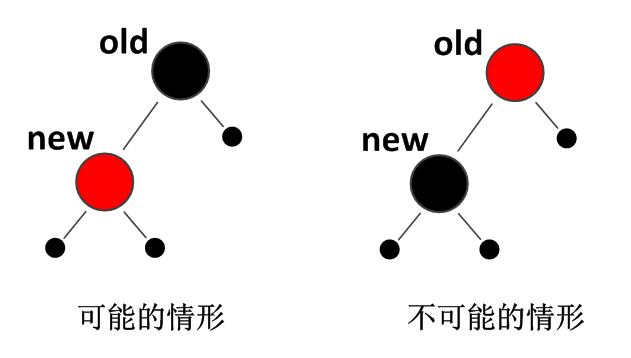
- old和new都是红色的,由红黑树定义可知,这是不可能的。
- old和new一红一黑,那么old必定为黑,因为如果old为红且其有一个孩子,那么其孩子节点必为黑色,那么old节点的左右子树的黑节点个数将不相等,这违反了红黑树的基本设定。
-
old和new都是黑色的,这个情况比较复杂,可继续细分为:
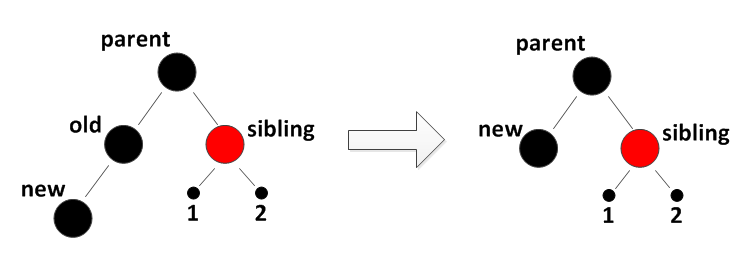
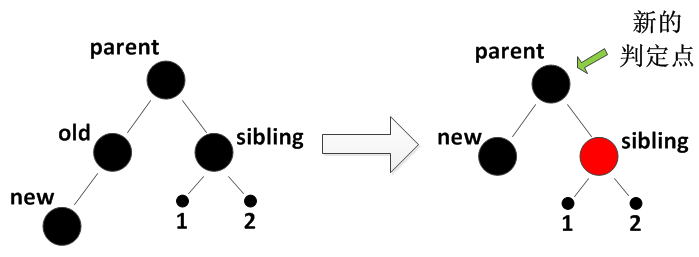
3.1 old的兄弟节点是红色的,如:
old的兄弟节点是红色的情形
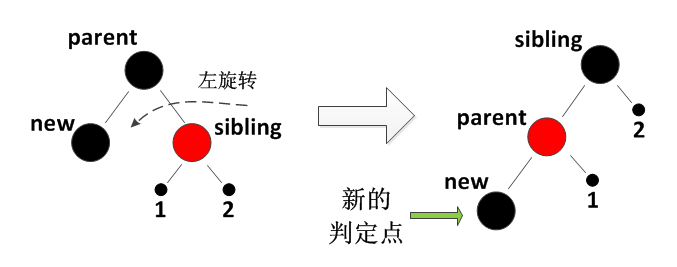
这种情况下,父节点一定是黑色的。接下来需要先将红色兄弟节点做左旋转,将原来的父节点压下去变成左孩子,并且交换父节点和兄弟节点的颜色,变成:
对红兄弟节点的操作
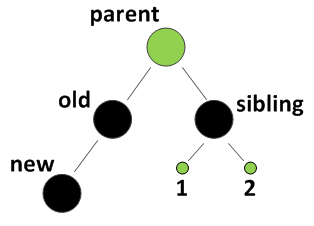
3.2 old的兄弟节点是黑色的,如:
old的兄弟节点是黑色的情形
图中parent和两个old的侄子节点都是绿色的,代表他们的颜色不确定,要继续细分所有的情形:
- 黑侄的情形
- 红父+双黑侄
- 黑父+双黑侄
具体而言,这些情形的图像展示是这样的:
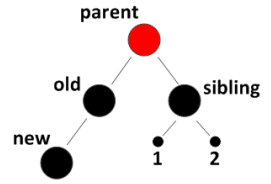
红父+双黑侄
此种情形比较简单,只需要将parent和sibling的颜色交换即可。
黑父+双黑侄
在黑父+双黑侄的情形下也较为简单,先将sibling翻转为红色,然后针对parent重新判定红黑树约束条件即可。
- 红侄的情形
- 同边红侄
- 对边红侄
- 双红侄
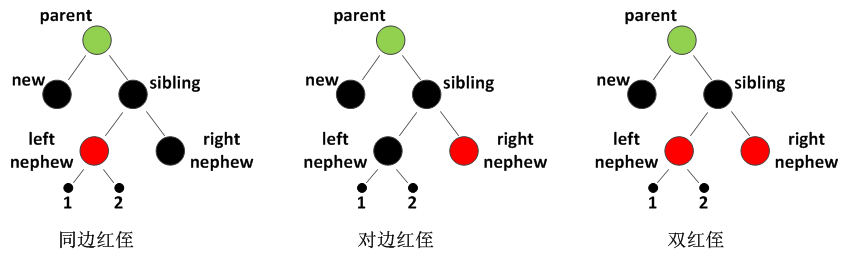
同边、对边的意思是,如果new及其侄子节点同属左节点或右节点,我们称他们为同边的,否则称为对边:
红侄的三种情形
当然,上述均是以new为左节点来讨论的情形,换成右节点的话是完全对称的,不再赘述。下面使用图画的方式,展现这些情形的解决办法:
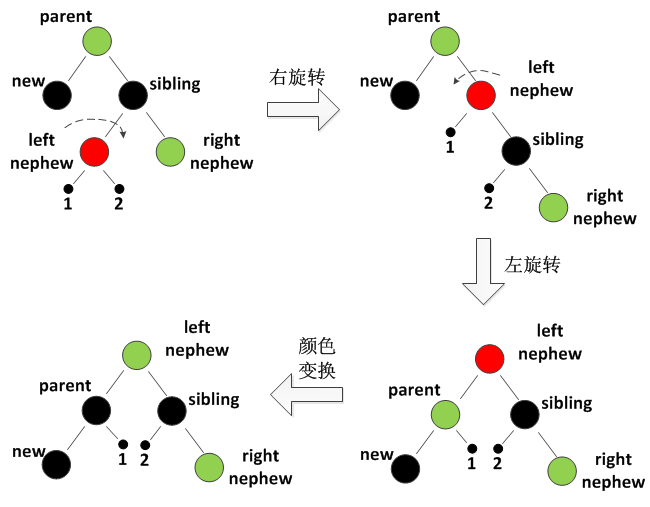
- 同边红侄的操作
同边红侄的操作
注意,同边红侄的操作过程中,并不需要嘉定对边侄子节点的颜色,因此本算法也囊括了所谓双边红侄的情况。
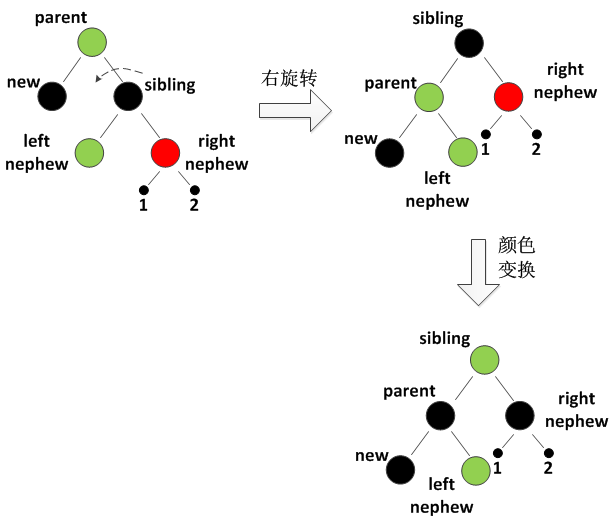
- 对边红侄的操作
对边红侄的操作
至此,红黑树删除节点的所有情形就全部讨论完毕了,接下来就是针对这些不同的情形编码实现。
删除红黑树节点的代码实现
linktree rbFind(linktree root, tn_datatype data)
{
if(root == NULL)
return NULL;
if(data < root->data)
return rbFind(root->lchild, data);
else if(data > root->data)
return rbFind(root->rchild, data);
return root;
}
void deleteFixup(linktree *proot, linktree new, linktree parent)
{
linktree ln, rn; // left nephew & right nephew
linktree s, gp; // sibling & grandparent
ln = rn = s = gp = NULL;
if(new == NULL && parent == NULL) // 原来的old是树都唯一节点
{
*proot = NULL;
return;
}
else if(new != NULL && parent == NULL) // 原来的old是根节点
{
*proot = new;
return;
}
else if(parent != NULL)
{
s = parent->lchild ? parent->lchild : parent->rchild;
gp = parent->parent;
if(s != NULL)
{
ln = s->lchild;
rn = s->rchild;
}
}
//1,红兄
if(Color(s) == RED)
{
if(new == parent->lchild)
{
rbRotateLeft(proot, s);
parent->color = RED;
s->color = BLACK;
deleteFixup(proot, new, parent);
}
if(new == parent->rchild)
{
rbRotateRight(proot, s);
parent->color = RED;
s->color = BLACK;
deleteFixup(proot, new, parent);
}
}
//2,黑兄
if(Color(s) == BLACK)
{
//2.1,黑兄,二黑侄,红父
if(Color(parent) == RED &&
Color(ln) == BLACK &&
Color(rn) == BLACK)
{
parent->color = BLACK;
if(s != NULL)
s->color = RED;
return;
}
//2.2,黑兄,二黑侄,黑父
if(Color(parent) == BLACK &&
Color(ln) == BLACK &&
Color(rn) == BLACK)
{
if(s != NULL)
{
s->color = RED;
}
deleteFixup(proot, parent, parent->parent);
}
//2.3,黑兄,同边红侄(同为左孩子)
if(Color(ln) == RED && new == parent->lchild)
{
rbRotateRight(proot, ln);
rbRotateLeft(proot, ln);
ln->color = parent->color;
parent->color = BLACK;
}
// (同为右孩子)
else if(Color(rn) == RED && new == parent->rchild)
{
rbRotateLeft(proot, rn);
rbRotateRight(proot, rn);
rn->color = parent->color;
parent->color = BLACK;
}
// 对边红侄(左右)
else if(Color(ln) == RED && new == parent->rchild)
{
rbRotateRight(proot, s);
s->color = parent->color;
parent->color = BLACK;
ln->color = BLACK;
}
// 对边红侄(右左)
else if(Color(rn) == RED && new == parent->lchild)
{
rbRotateLeft(proot, s);
s->color = parent->color;
parent->color = BLACK;
rn->color = BLACK;
}
}
}
void realDelete(linktree *proot, linktree old)
{
// old不可能为NULL,new可能为NULL
linktree new = old->lchild ? old->lchild : old->rchild;
linktree parent = old->parent;
if(old->parent != NULL)
{
if(old == old->parent->lchild)
old->parent->lchild = new;
else
old->parent->rchild = new;
old->parent = NULL;
}
if(new != NULL)
new->parent = old->parent;
if(Color(old) == BLACK && Color(new) == RED)
{
new->color = BLACK;
}
else if(Color(old) == BLACK && Color(new) == BLACK)
{
deleteFixup(proot, new, parent);
}
free(old);
}
void rbDelete(linktree *proot, tn_datatype data)
{
// 进行传统 BST 删除逻辑
linktree tmp = rbFind(*proot, data);
if(tmp == NULL)
{
printf("%d is NOT exist.\n", data);
return;
}
linktree n = tmp;
if(tmp->lchild != NULL)
{
n = tmp->lchild;
for(;n->rchild != NULL; n = n->rchild);
tmp->data = n->data;
}
else if(tmp->rchild != NULL)
{
n = tmp->rchild;
for(;n->lchild != NULL; n = n->lchild);
tmp->data = n->data;
}
// 判定红黑树逻辑约束
realDelete(proot, n); // n has ONE red-child at most
}