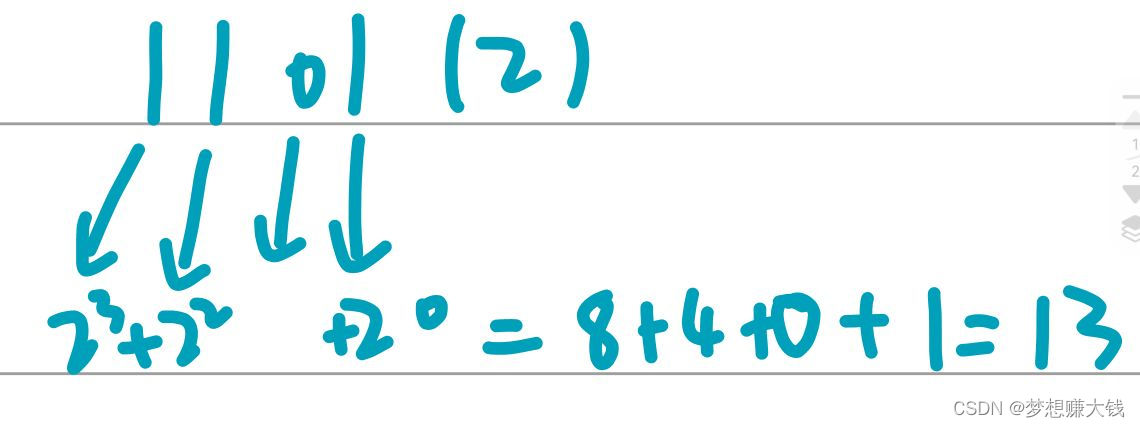一、什么是背包问题

   有一个固定体积的背包，以及若干具有体积和价值的物品。求装哪几件物品可以使得背包内价值最大。也有背包承受的重量固定，求最大价值之类的，换汤不换药，这里我们以体积和价值作为例子。
注意：不一定要装满背包

二、背包问题的分类

1. 0 1背包问题

为什么要叫01背包呢，是因为一个物品只能拿零次或者一次，不可以拿其中一部分，也不可以多次拿。每件物品只能用一次。

解决这个问题我们用到的方法是动态规划（DP），首先我们讲解一个容易理解的二维版本：

定义一个二维数组dp[i][j],其中i代表从选择的物体在前i个当中，j表示现在背包装的最大体积。dp[i][j]的值代表现在背包内的价值。

v[i]代表第i个物品的体积，w[i]代表第i个物品的质量

当面临选择第i个物品的时候，我们无非就是两种选择，选或者是不选

那么我们只要从这两种方法里面选出来大的那个，就是问题的解决方案

由此可以得出来一个公式dp[ i ][ j ]=max(dp[ i-1 ][ j ],dp[ i-1,j-v[ i ]]+w[ i ]);

于是我们可以遍历这个二维数组，从第一个到最后一个物品，从没有容量到背包的容量

格子里面的数代表dp[i][j](表没画完）

代码如下：

import java.util.*;

public class Main{
    public static void  main(String args[]){
        Scanner scan=new Scanner(System.in);
        int N=scan.nextInt();
        int V=scan.nextInt();
        int v[]=new int[1010];
        int w[]=new int[1010];
        int dp[][]=new int[N+1][V+1];
        dp[0][0]=0;
       
       for(int i=1;i<=N;i++)
       {
           v[i]=scan.nextInt();
           w[i]=scan.nextInt();
       }
       for(int i=1;i<=N;i++)
       {
           for(int j=0;j<=V;j++)
           {
               
               if(j>=v[i]){
                  dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-v[i]]+w[i]);
               }else{
                   dp[i][j]=dp[i-1][j];
               }
           }
       }
        
        System.out.println(dp[N][V]);
    }
}

中间的判断条件是为了判断能不能放得下

接下来我们讲解优化一维版本：
这里用到一个概念：滚动数组，滚动数组就是新数据代替旧数据，不需要开发新的空间来存储，在同一组空间上不断覆盖，因为我们只需要最后的结果，所以可以使用这种方法。

这里我们在打表的时候，下一个数据覆盖上一行数据，我们就省去了遍历行这一步，只遍历列。

我们的核心代码就从上面的那个变成了下面这个。01背包在使用滚动数组的时候，是从右往左遍历。（为什么要从右向左呢？在讲完完全背包之后给大家解释，两个对比着学更容易理解）。

代码：

import java.util.*;

public class Main{
    public static void  main(String args[]){
        Scanner scan=new Scanner(System.in);
        int N=scan.nextInt();
        int V=scan.nextInt();
        int v[]=new int[1010];
        int w[]=new int[1010];
        int dp[]=new int[V+1];
 
       for(int i=1;i<=N;i++)//输入各物体的体积和价值
       {
           v[i]=scan.nextInt();
           w[i]=scan.nextInt();
       }
       
       for(int i=1;i<=N;i++)
       {
           for(int j=V;j>=0;j--)
           {
               if(j>=v[i]){
                  dp[j]=Math.max(dp[j],dp[j-v[i]]+w[i]);
               }else{
                   dp[j]=dp[j];
               }
           }
       }
        
        System.out.println(dp[V]);
    }
}

有同学可能或疑惑，为什么由二维降成一维了，还是两层循环呢，是因为我们省去了数组的行遍历，但是我们仍然需要用到第i个物体的体积和价值

2.完全背包问题

 定义：每件物品可以用无限次，每个物品可以被使用的下限是0，上限是j除以w[i]向下取整;
那我们就可以把这些物体看成是一个一个的物体，对每一种物品，都加一个从0到（j/w[i]）的遍历。这样子我们就把一个完全背包问题转换成了01背包问题。这是优化前的解法。

代码：

import java.util.*;

public class Main{
    public static void  main(String args[]){
        Scanner scan=new Scanner(System.in);
        int N=scan.nextInt();
        int V=scan.nextInt();
        int v[]=new int[1010];
        int w[]=new int[1010];
        int dp[][]=new int[1010][1010];
       
       for(int i=1;i<=N;i++)
       {
           v[i]=scan.nextInt();
           w[i]=scan.nextInt();
       }
       
       for(int i=1;i<=N;i++)
       {
           for(int j=0;j<=V;j++)
           {
              for(int k=0;k*v[i]<=j;k++)
                  dp[i][j]=Math.max(dp[i][j],dp[i-1][j-k*v[i]]+k*w[i]);

           }
       }
        
        System.out.println(dp[N][V]);
    }
}

优化部分：

【图截自b站】

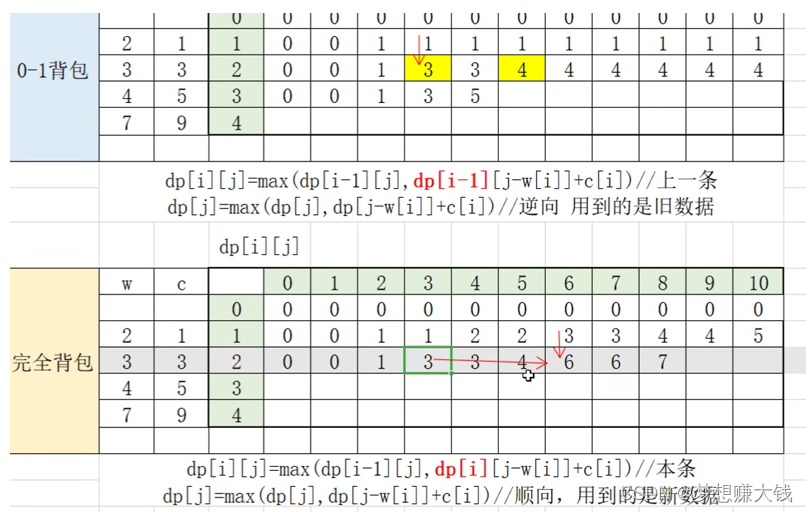
  优化后的核心代码与01背包一样，不一样的点在于他们的遍历顺序。01背包从后往前遍历，完全背包从前往后遍历。

为什么01是从后往前呢？

   因为01背包不可以取同一种物品，所以二维来说它的数据是从上一行来的。从一维来说它左边的数据才是旧数据，所以我们要用到左边的数据。如果从左往右遍历的话，我们会覆盖掉旧的数据，导致后面的数据出错。

为什么完全背包是从前往后呢？

因为可以取同一种物品，所以数据是可以从同一行来的，我们要先确认了前面的数据，才能确认后面的数据。

3.多重背包

   每件物品可以用s[i]次，每个物品的个数不一样 。我们把物品划分成一个一个的，这样就转化成了01背包问题。这样是未优化的方式，这样做的话，数据多的时候无法正常通过测试。所以接下来为大家介绍优化的方法：

  我们都知道二进制和十进制是可以互相转化的，每一个十进制数都可以用一个二进制数来表示。二进制数转十进制的时候，每一位都代表一个二的次数。比如说：

      所以我们可以把多重背包的数按2的次数分成若干倍打包。s[i]个物体分成(v,w)（2v,2w），（4v,4w）。。。。。被分到一组的物品看成是一个整体。这样这个问题就再次被转换成了01背包问题。

代码如下：

java.util.Scanner;
public class Main{
    public static void main(String[] args){
        Scanner scan = new Scanner(System.in);
        int N = scan.nextInt();
        int V = scan.nextInt();
        int[] ans = new int[V+1];
        for(int i = 0 ; i < N;i++){
            int w = scan.nextInt();
            int val = scan.nextInt();
            int sum = scan.nextInt();
            int k = 1;//每次分组的物品个数
            while(sum > 0){
                if(sum - k < 0){//剩下不够分一组，拿剩下的做一次01背包
                    for(int j = V;j >= w * sum ;j--){
                        ans[j] = Math.max(ans[j],ans[j - w * sum] + val * sum);
                    }
                    break;
                }
                for(int j = V;j >= w * k ;j--){//剩下够分一组，拿k个物品做一次01背包
                    ans[j] = Math.max(ans[j],ans[j - w * k] + val * k);
                }
                sum -= k;
                k *= 2;
            }
        }
        System.out.println(ans[V]);
    }
}

4.分组背包
   每一组有若干个物品，每一组最多选一个物品,若一个组有m个物品，则有m+1中选法。1.。。。m,以及全不选。在01背包的基础上遍历一下组内的物品。同时在录入数据的时候使用二维数组。这样就可以解决了

for(int i=0;i<n;i++)
{
    for(int j=m;j>=0;j--)
    {
        for(int k=0;k<s[i];k++)
        { 
             if(j>=v[i][k])     f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);  
        }
    }
}