接下来的题目有些地方比较相似。需要注意多个条件。
题目:分发糖果
n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。
你需要按照以下要求,给这些孩子分发糖果:
- 每个孩子至少分配到
1个糖果。 - 相邻两个孩子评分更高的孩子会获得更多的糖果。
请你给每个孩子分发糖果,计算并返回需要准备的 最少糖果数目 。
题目分析:
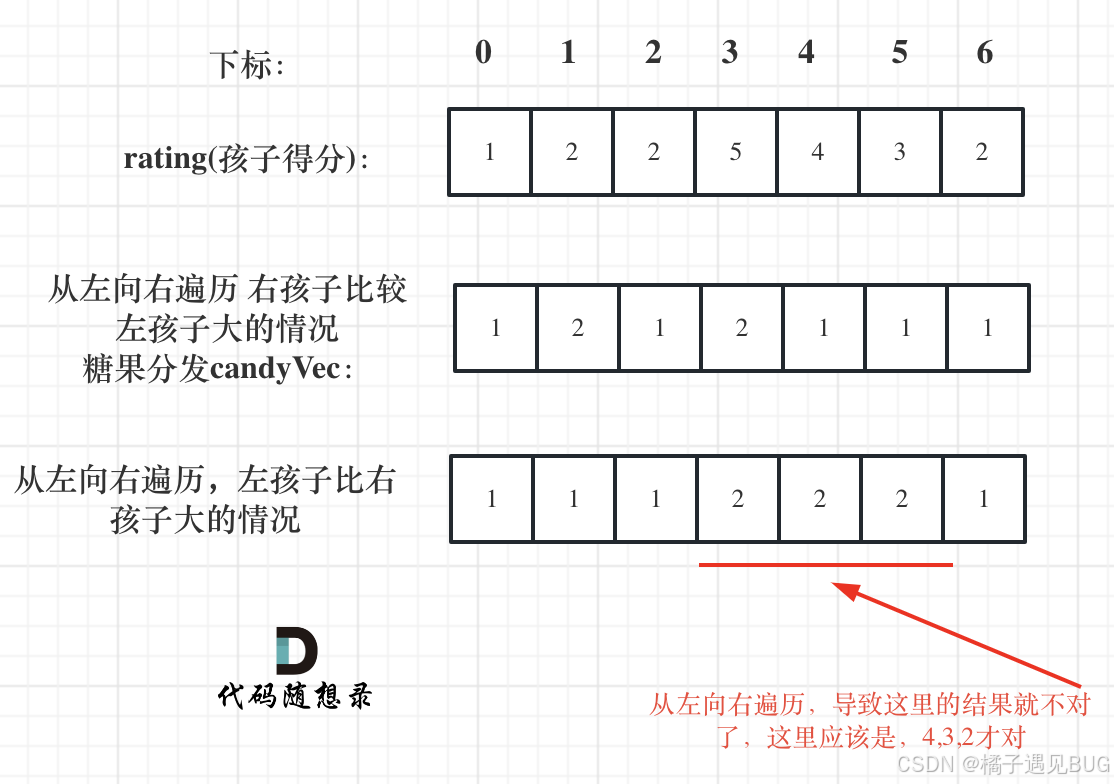
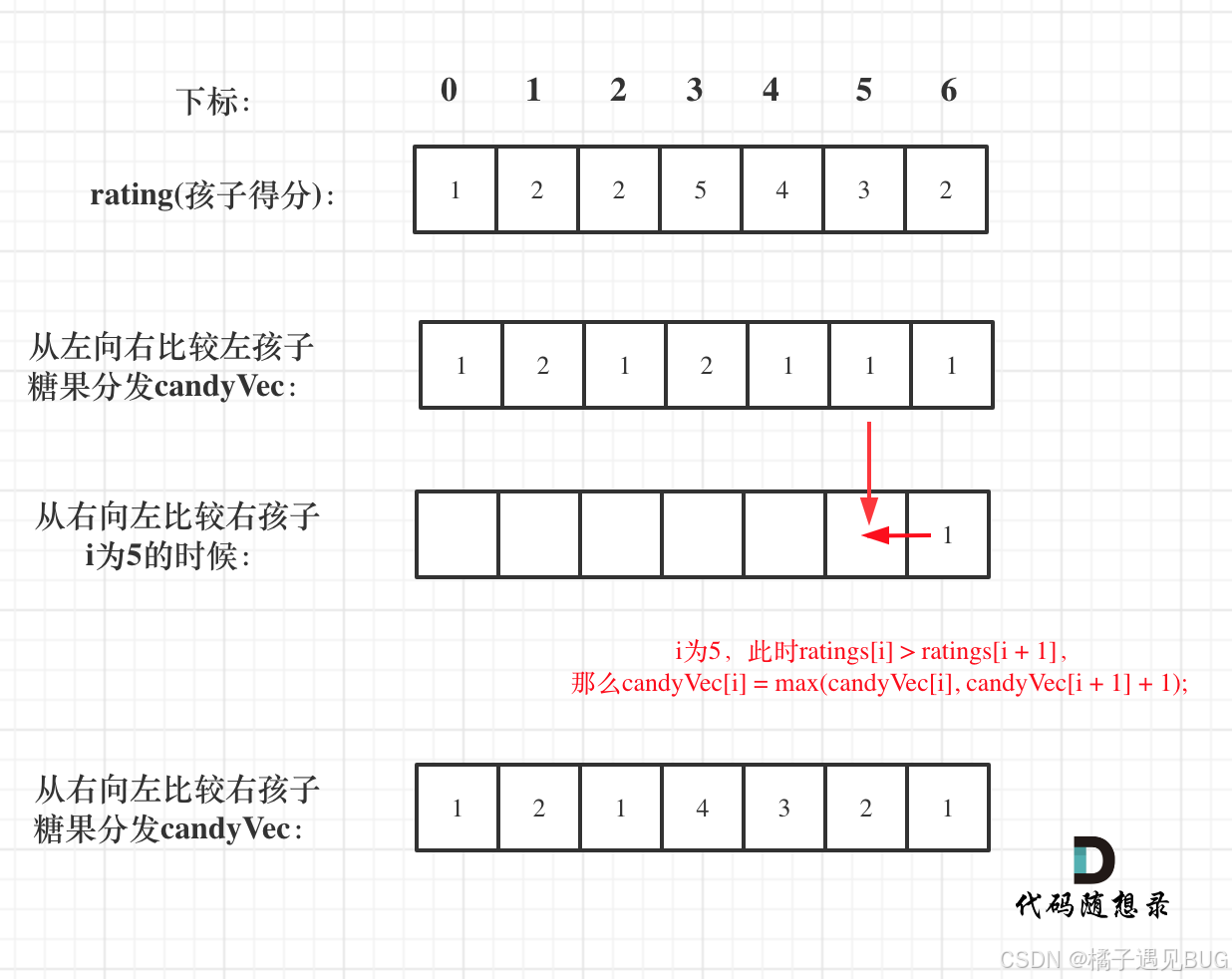
分发糖果需要考虑左右两边的大小,不能同时考虑,会很乱。那么就先考虑一边,在考虑另外一边。
那么就变成了,从前向后看,比较右孩子大于左孩子的情况和从后往前看,比较左孩子大于右孩子的情况。之所以第二个条件需要从后往前的原因,是因为继续从前往后会不满足题目。
就像这样
所以需要从后往前
代码如下:
public class Solution {
public int Candy(int[] ratings) {
int[] res=new int[ratings.Length];
int candys=0;
for(int i=0;i<res.Length;i++){
res[i]=1;//所有孩子最低都是1
}
//因为比较需要考虑左右两边的情况,所以需要分开考虑(两个条件)
for(int i=1;i<ratings.Length;i++){//从前向后看,比较右孩子大于左孩子的情况
if(ratings[i]>ratings[i-1]){
res[i]=res[i-1]+1;
}
}
for(int i=ratings.Length-2;i>=0;i--){//从后往前看,比较左孩子大于右孩子的情况
if(ratings[i]>ratings[i+1]){
res[i]=Math.Max(res[i],res[i+1]+1);
}
}
for(int i=0;i<res.Length;i++){
candys+=res[i];
}
return candys;
}
}题目:根据身高重建队列
假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki 个身高大于或等于 hi 的人。
请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ,其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性(queue[0] 是排在队列前面的人)。
题目分析:
同样的需要满足两个条件,那就一个一个的考虑。我们根据身高进行从大到小的排列,身高相同的就根据k进行从小到达的排列。至于为什么这样排,结合题目要求来看
那么代码就很好写出来了
public class Solution {
public int[][] ReconstructQueue(int[][] people) {
//需要考虑两个条件,分开考虑
//先根据身高从大到小排序,这样插入的时候不用考虑K,
//因为排序之后这个值后面的值一定比他小,在前面插入小的值,自然影响不到他
Array.Sort(people,(a,b)=>{
if(a[0]==b[0]){//同样的身高,根据k排序,从小到大
return a[1]-b[1];
}
else return b[0]-a[0];
});
var res = new List<int[]>();
for(int i=0;i<people.Length;i++){//根据k直接插入
res.Insert(people[i][1],people[i]);
}
return res.ToArray();
}
}题目:用最少数量的箭引爆气球
有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ,其中points[i] = [xstart, xend] 表示水平直径在 xstart 和 xend之间的气球。你不知道气球的确切 y 坐标。
一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一支箭,若有一个气球的直径的开始和结束坐标为 xstart,xend, 且满足 xstart ≤ x ≤ xend,则该气球会被 引爆 。可以射出的弓箭的数量 没有限制 。 弓箭一旦被射出之后,可以无限地前进。
给你一个数组 points ,返回引爆所有气球所必须射出的 最小 弓箭数 。
题目分析:
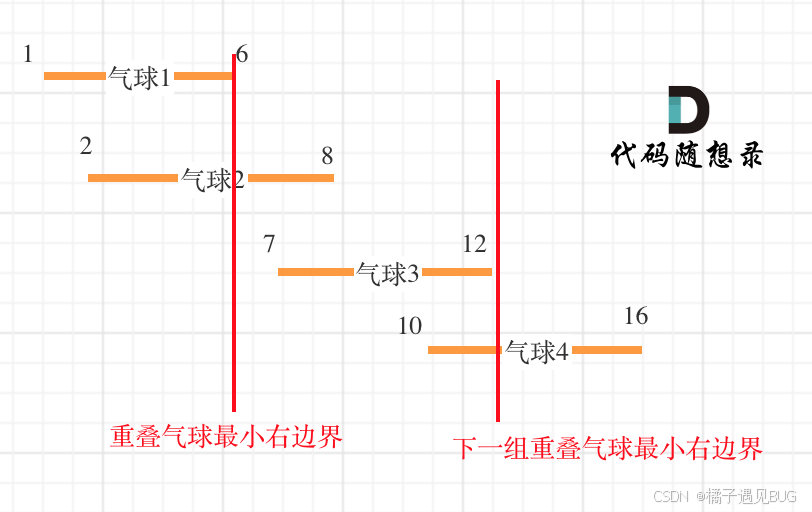
根据题目的意思,气球的摆放是有重叠的,如何使用更少的弓箭,自然就是从重叠下手。
就像这样
看看代码理解
public class Solution {
public int FindMinArrowShots(int[][] points) {
Array.Sort(points,(a,b)=>a[0].CompareTo(b[0]));
int res=1;
for(int i=1;i<points.Length;i++){
if(points[i][0]>points[i-1][1])//后面气球的起点超过了这个气球的终点,气球不相交
res++;
else{//气球重贴了,就把两个气球的范围合起来
points[i][1]=Math.Min(points[i-1][1],points[i][1]);// 更新重叠气球最小右边界
}
}
return res;
}
}题目分析:无重叠区间
给定一个区间的集合 intervals ,其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量,使剩余区间互不重叠 。
注意 只在一点上接触的区间是 不重叠的。例如 [1, 2] 和 [2, 3] 是不重叠的。
题目分析:
和上一题其实差不多的,那么排序的时候我们选择左边界排序还是右边界排序呢?其实都是没有问题的,
假如我们根据有边界排序,从左向右记录非交叉区间的个数。最后用区间总数减去非交叉区间的个数就是需要移除的区间个数了。
如果根据左边界排序,就是直接求 重叠的区间,count为记录重叠区间数
public class Solution {
public int EraseOverlapIntervals(int[][] intervals) {
if (intervals.Length == 0) return 0;
Array.Sort(intervals, (a, b) => a[1].CompareTo(b[1]));
int res = 1, end = intervals[0][1];
for (int i = 1; i < intervals.Length; i++)
{
if (end <= intervals[i][0])
{
end = intervals[i][1];
res++;
}
}
return intervals.Length - res;
}
}题目:划分字母区间
给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。
注意,划分结果需要满足:将所有划分结果按顺序连接,得到的字符串仍然是 s 。
返回一个表示每个字符串片段的长度的列表。
题目分析:
这一题可以使用hash去统计字符的位置,但是这样很容易超时。
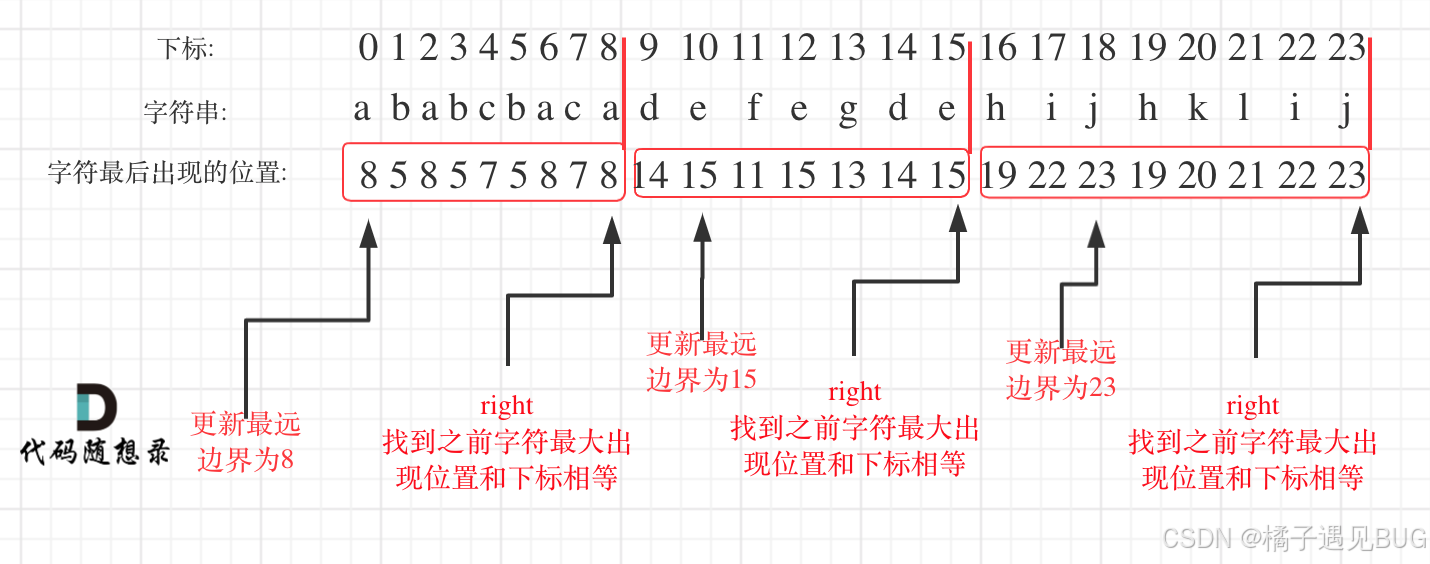
在遍历的过程中相当于是要找每一个字母的边界,如果找到之前遍历过的所有字母的最远边界,说明这个边界就是分割点了。此时前面出现过所有字母,最远也就到这个边界了。
可以分为如下两步:
- 统计每一个字符最后出现的位置
- 从头遍历字符,并更新字符的最远出现下标,如果找到字符最远出现位置下标和当前下标相等了,则找到了分割点
代码如下:
public class Solution {
public IList<int> PartitionLabels(string s) {
int[] location = new int[27];
for (int i = 0; i < s.Length; i++)//记录每个元素出现的最远位置
{
location[s[i] - 'a'] = i;
}
List<int> res = new List<int>();
int left = 0, right = 0;
for (int i = 0; i < s.Length; i++)
{
right = Math.Max(right, location[s[i] - 'a']);//更新这个区间的最远位置
if (i == right)//到达最远位置,划分
{
res.Add(right - left + 1);
left = i + 1;
}
}
return res;
}
}题目:合并区间
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
题目分析:
和之前的题目差不多 ,排序之后比较
public class Solution {
public int[][] Merge(int[][] intervals) {
if (intervals.Length == 0)
return intervals;
Array.Sort(intervals,(a,b)=>{
return a[0]-b[0];//从小到大排列
});
List<List<int>> res = new List<List<int>>();
res.Add(intervals[0].ToList());
for(int i=1;i<intervals.Length;i++){
if(intervals[i][0]<=res[res.Count-1][1]){//和结果中最后一个区间重贴
res[res.Count-1][1]=Math.Max(intervals[i][1],res[res.Count-1][1]);
}
else{
res.Add(intervals[i].ToList());
}
}
return res.Select(x => x.ToArray()).ToArray();
}
}题目:单调递增的数字
当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时,我们称这个整数是单调递增的。
给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 单调递增 。
题目分析:
暴力解放比较简单,对每一个数进行判断,当然肯定会超时。看看贪心的思路,例如:98,一旦出现strNum[i - 1] > strNum[i]的情况(非单调递增),首先想让strNum[i - 1]--,然后strNum[i]给为9,这样这个整数就是89,即小于98的最大的单调递增整数。
此时是从前向后遍历还是从后向前遍历呢?
从前向后遍历的话,遇到strNum[i - 1] > strNum[i]的情况,让strNum[i - 1]减一,但此时如果strNum[i - 1]减一了,可能又小于strNum[i - 2]。
所以选择从后向前遍历。
public class Solution {
public int MonotoneIncreasingDigits(int n) {
char[] temp=n.ToString().ToCharArray();
int flag=temp.Length;//记录那些位置需要改变
for(int i=temp.Length-1;i>0;i--){
if(temp[i-1]>temp[i]){
flag=i;
temp[i-1]--;
}
}
for(int i=flag;i<temp.Length;i++){
temp[i]='9';
}
return int.Parse(new string(temp));
}
}对于更详细的解析与其他语言的代码块,可以去代码随想录上查看。
已刷题目:86