前景回顾/提出问题
回顾1
首先回顾一下DVD在线租赁问题
在 question2中,需要保证每个人都不会收到自己不喜欢的DVD,即客户在线订单数为0时候,不可以租给他。我直接给出答案了:
x
i
j
≤
o
r
d
e
r
i
j
,
i
=
1
,
2
,
3
,
.
.
n
,
j
=
1
,
2
,
3
,
.
.
m
x_{ij} \le order_{ij} ,i=1,2,3,..n , j= 1,2,3,..m
xij≤orderij,i=1,2,3,..n,j=1,2,3,..m
实际思路其实是
如果
o
r
d
e
r
i
j
=
0
order_{ij} = 0
orderij=0,那么
x
i
j
=
0
x_{ij} = 0
xij=0, 也就是说客户不喜欢我决定不租
反之
o
r
d
e
r
i
j
>
0
order_{ij} \gt 0
orderij>0,那么
x
i
j
=
0
/
1
x_{ij} = 0/1
xij=0/1,也就是说客户喜欢我自己决定租还是不租。
列表找规律还是尝试不同的不等式都可以在比较短的时间内想出正确答案。
回顾2/问题提出
接下来回顾一下天然肠衣搭配问题
其中手动进行局部最优解的时候,还有一个附带问题:
已知原料能捆137个成品三,那么用到最少种配方数是多少?
例如我用到了73种配方我就可以完成137个成品三,那么同样是做137个成品三,就比用到100种配方少。
当时求最多能捆多少个成品三的模型为:
设使用方案
i
i
i的次数为
y
i
y_i
yi,原料按长度由小到大的总个数依次为
d
1
d
2
,
.
.
.
,
d
n
d_1 d_2 ,...,d_n
d1d2,...,dn
方案总数为
a
a
a;方案
i
i
i使用第
j
j
j种原料数量为
z
i
j
z_{ij}
zij
对于每一个原料我们都得
d
i
≥
∑
1
≤
j
≤
a
y
j
∗
z
j
i
,
1
≤
i
≤
n
d_i \ge \sum_{1 \le j \le a} y_j*z_{ji} , 1\le i \le n
di≥∑1≤j≤ayj∗zji,1≤i≤n
求
max
∑
1
≤
i
≤
a
y
i
\max \sum_{1\le i \le a}y_i
max∑1≤i≤ayi
现在
max
∑
i
=
1
a
y
i
\max \displaystyle\sum_{i=1}^{a}y_i
maxi=1∑ayi变成了
∑
i
=
1
a
y
i
=
137
\displaystyle\sum_{i=1}^{a}y_i = 137
i=1∑ayi=137
求解问题也变成了求
max
∑
i
=
1
a
y
i
>
0
\max \displaystyle\sum_{i=1}^{a}y_i\gt 0
maxi=1∑ayi>0
如果借鉴DVD在线租赁问题的思路就是,
f
i
f_i
fi为0/1变量
如果
y
i
>
0
y_i \gt 0
yi>0,那么
f
i
=
1
f_i = 1
fi=1 ,用了这种配方就
反之
y
i
=
0
y_i = 0
yi=0,那么
f
i
=
0
/
1
f_i = 0/1
fi=0/1 , 没用这种配方
求
min
∑
i
=
1
a
f
i
\min \displaystyle\sum_{i=1}^{a} f_i
mini=1∑afi
因为是求最小值(
f
i
f_i
fi自动取最小的那一个),所以实际上如果
y
i
=
0
y_i = 0
yi=0,那么
f
i
=
0
f_i = 0
fi=0是绝对成立的
但这一次就没那么简单了,不是简单的
y
i
≤
f
i
y_i\le f_i
yi≤fi 或者
y
i
≥
f
i
y_i\ge f_i
yi≥fi,所以不能轻易的得出答案
所以问题就是这个限制条件怎么写?
解决前提
1.不能破坏线性规划模型,即不能出现变量和变量相乘的情况
2.
如果
y
i
>
0
y_i \gt 0
yi>0,那么
f
i
=
1
f_i = 1
fi=1 ,用了这种配方就
反之
y
i
=
0
y_i = 0
yi=0,那么
f
i
=
0
/
1
f_i = 0/1
fi=0/1 , 没用这种配方
解决上面描述很容易想到用
i
f
if
if语句,这里也不可以,也就是下面这种模型
f
i
=
{
1
,
y
i
>
0
1
,
y
i
=
0
f_i = \begin{cases}1,y_i \gt 0\\1,y_i = 0\end{cases}
fi={1,yi>01,yi=0
解决方法
坐标轴(区间)法
线性规划中
a
≤
b
a\le b
a≤b和
a
≥
b
a\ge b
a≥b是最常用的,也是能很好的约束
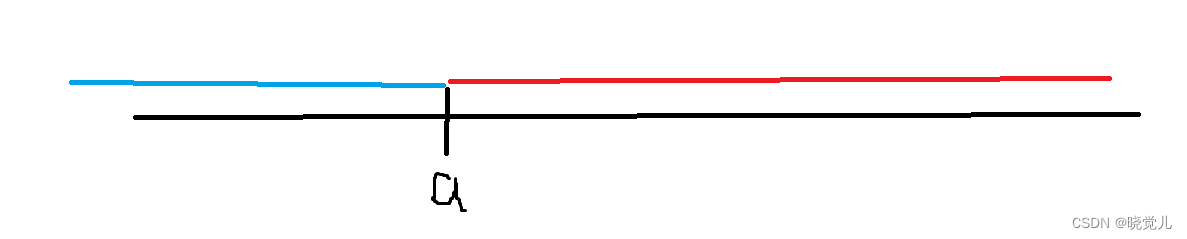
基本概念
≤
a
\le a
≤a和
≥
a
\ge a
≥a分别是蓝色线和红色线表示的区间
解决天然肠衣搭配问题
那么变形一下上面的判断描述
如果
y
i
>
0
y_i \gt 0
yi>0,那么
f
i
=
1
f_i = 1
fi=1 ,用了这种配方就
反之
y
i
≤
0
y_i \le 0
yi≤0,那么
f
i
=
0
/
1
f_i = 0/1
fi=0/1 , 没用这种配方
如果定义
≥
y
\ge y
≥y,
y
y
y分
y
1
>
0
y_1\gt 0
y1>0和
y
2
=
0
y_2 = 0
y2=0
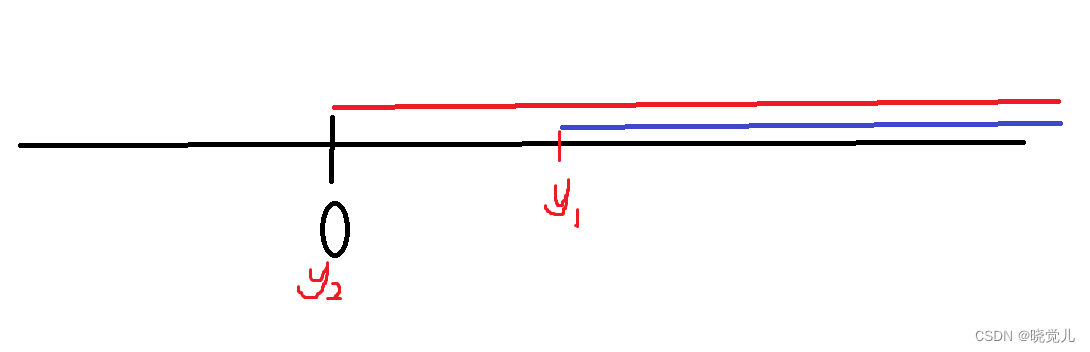
就会出现以下两个区间,红色:
≥
y
2
\ge y_2
≥y2 , 蓝色:
≥
y
1
\ge y_1
≥y1
通过画图分析发现蓝色区间不包含0,也就是说只要我
y
i
>
0
y_i \gt 0
yi>0 时候,要求
f
i
>
y
i
f_i \gt y_i
fi>yi就能限制住
f
i
>
0
f_i \gt 0
fi>0,即
f
i
f_i
fi不可能有0的取值了
而红色区间,带入同样的限制
f
i
>
y
i
f_i \gt y_i
fi>yi,得到
f
i
≥
0
f_i \ge 0
fi≥0,即
f
i
=
0
/
1
f_i = 0/1
fi=0/1和我们描述相符
现在问题就来了,虽然
y
i
>
0
y_i \gt 0
yi>0 时候
f
i
f_i
fi不可能有0的取值了但也不能取1!
也就是说我
f
i
f_i
fi还必须落在蓝色区域里,如果
y
i
≤
+
∞
y_i\le +\infin
yi≤+∞那就完蛋了,满足的式子只有
f
i
y
i
>
y
i
f_iy_i \gt y_i
fiyi>yi或者
y
i
≤
+
∞
f
i
y_i \le +\infin f_i
yi≤+∞fi,分别不满足解决前提2和不现实
但已知还有一个条件
∑
i
=
1
a
y
i
=
137
\displaystyle\sum_{i=1}^{a}y_i = 137
i=1∑ayi=137,可以得出
y
i
≤
137
y_i \le 137
yi≤137
那么
137
f
i
>
y
i
137f_i \gt y_i
137fi>yi 这个限制条件就可以让,
f
i
f_i
fi取1。
综上所述,
137
f
i
137f_i
137fi当
f
i
=
1
f_i=1
fi=1落在蓝色和红色区间,但当
f
i
=
0
f_i=0
fi=0只落在红色区间,也就完成了线性的限制约束条件。
这时候同样的方法重做DVD在线租赁问题
已知:
如果
o
r
d
e
r
i
j
=
0
order_{ij} = 0
orderij=0,那么
x
i
j
=
0
x_{ij} = 0
xij=0, 也就是说客户不喜欢我决定不租
反之
o
r
d
e
r
i
j
>
0
order_{ij} \gt 0
orderij>0,那么
x
i
j
=
0
/
1
x_{ij} = 0/1
xij=0/1,也就是说客户喜欢我自己决定租还是不租。
改变加简化为
如果
o
r
i
≤
0
or_i \le 0
ori≤0,那么
x
i
=
0
x_i = 0
xi=0, 也就是说客户不喜欢我决定不租
反之
o
r
i
>
0
or_i \gt 0
ori>0,那么
x
i
=
0
/
1
x_i = 0/1
xi=0/1,也就是说客户喜欢我自己决定租还是不租。
因为限制
o
r
i
≤
0
or_i \le 0
ori≤0时候
x
i
x_i
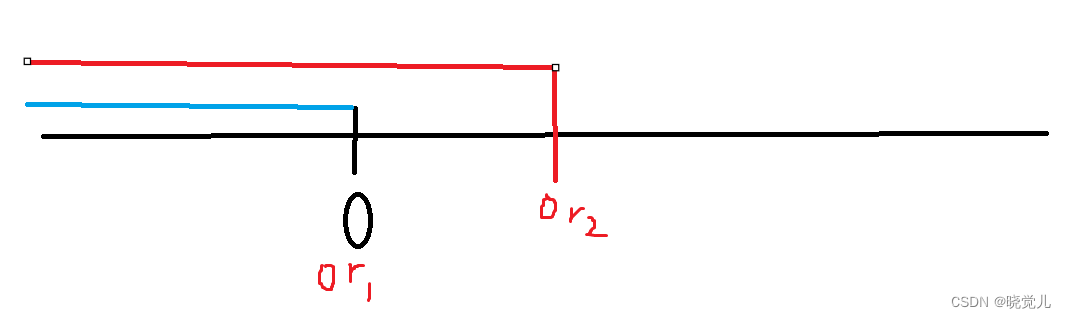
xi不能取1,所以在数轴上画出0坐标,考虑如果区间是往右延申是不会包括1的,所以定义
≤
o
r
i
\le or_i
≤ori
注意:定义和最终限制往往是同号!
通过图分析可得 x i ≤ o r i x_i \le or_i xi≤ori是满足条件的约束,并且也不存在说如果 o r i ≤ + ∞ or_i\le +\infin ori≤+∞那就完蛋了因为 x i ≤ o r i ≤ + ∞ x_i \le or_i \le +\infin xi≤ori≤+∞
而上面的是需要 y i ≤ f i y_i \le f_i yi≤fi ,只能 y i ≤ + ∞ f i ≤ + ∞ y_i \le +\infin f_i \le +\infin yi≤+∞fi≤+∞,明显是无法求解的
总结
线性规划的条件可以利用区间来表示范围,数轴则是更加清晰
0/1变量两个取值实际上就是数轴上的两个点
例如
a
f
i
+
b
af_i+b
afi+b,当
f
i
f_i
fi取0/1实际上就是b和a+b两个点
而
≤
\le
≤和
≥
\ge
≥表示是区间
一般分析过后适当做线性变化即可得到想要的线性限制条件