作用

1、将两个集合合并

2、查询两个集合是否在一个集合中

暴力做法：

belong[x] = a
//存储的是x属于哪个集合
//=a 表示的是属于a这个集合

//2、查询两个集合是否在一个集合中
if(belong[x] == bbelong[y])
//时间复杂度为O(1)

//1、将两个集合合并
//假设想合并的第一个集合里面有1000个元素，第二个集合里面有2000个元素
//要么是将第一个集合中属于的那个编号改成第二个集合中的子编号，要么换一下，
起码需要1000次计算

但是并查集可以在近乎O(1)的时间复杂度完成这两个操作

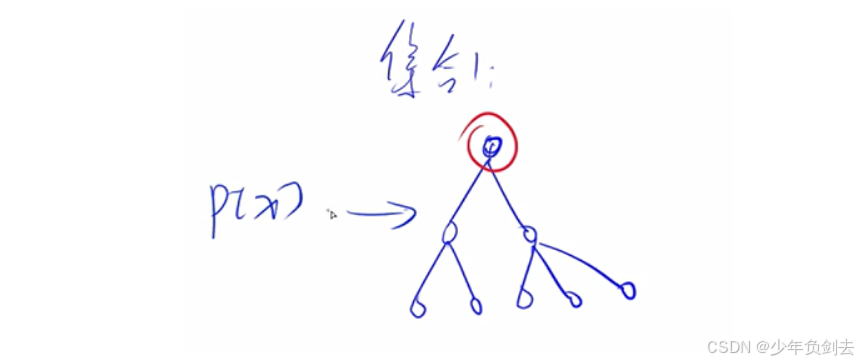
基本原理：

每个集合都用一棵树来表示，树根的编号就是整个集合的编号。每个节点存储他的父节点，p[x]表示x的父节点。

1、每一个集合都是用树的形式来维护

2、每一个集合的编号都是根节点的编号

3、对于集合中的每一个点 都去存储他的父节点是谁 p[x] 是指x节点的父节点是谁

代码分析：

//找到元素的根节点
int find(int x)//返回x的祖宗节点 + 路径压缩
{
    if( p[x] != x) //x不是根节点
        p[x] = find(p[x]);
    return p[x];
}

题目：合并集合

一共有 n个数，编号是 1 ∼ n ，最开始每个数各自在一个集合中。

现在要进行 m个操作，操作共有两种：

1、 M a b，将编号为 a 和 b 的两个数所在的集合合并，如果两个数已经在同一个集合中，则忽略这个操作；
2、 Q a b，询问编号为 a 和 b 的两个数是否在同一个集合中；

输入格式

第一行输入整数 n 和 m 。

接下来 m 行，每行包含一个操作指令，指令为M a b或Q a b中的一种。

输出格式

对于每个询问指令Q a b，都要输出一个结果，如果 a和 b 在同一集合内，则输出 Yes，否则输出 No。

每个结果占一行。

数据范围

1 ≤ n ,m≤10^5

输入样例：

4 5
M 1 2
M 3 4
Q 1 2
Q 1 3
Q 3 4

输出样例：

Yes
No
Yes

代码

#include <iostream>
const int N = 100010;
int m,n,p[N];

//树根就是自己  当p[x] = x的时候 x就是树根

//返回元素的根节点
int find(int x)
{
	if (p[x] != x) p[x] = find(p[x]);
	return p[x];
}
int main()
{
	scanf("%d%d",&n,&m);
	//先让所有的节点的p值赋给自己
	for (int i = 1; i <= n; i++) p[i] = i;

	while (m--)
	{
		char op[2];
		int a, b;
		scanf("%s%d%d", op, &a, &b);
		if (op[0] == 'M') p[find(a)] = p[b]; // 让p[a]的父节点等于p[b]
		else
		{
			if (find(a) == find(b)) puts("Yes");
			else puts("No");
		}

	}
	return 0;
}