原题链接:B3644 【模板】拓扑排序 / 家谱树 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
题目:
题目描述
有个人的家族很大,辈分关系很混乱,请你帮整理一下这种关系。给出每个人的后代的信息。输出一个序列,使得每个人的后辈都比那个人后列出。
输入格式
第 1 行一个整数 𝑁(1≤𝑁≤100),表示家族的人数。接下来 𝑁 行,第 𝑖 行描述第 𝑖 个人的后代编号 𝑎𝑖,𝑗,表示 𝑎𝑖,𝑗是 𝑖 的后代。每行最后是 0 表示描述完毕。
输出格式
输出一个序列,使得每个人的后辈都比那个人后列出。如果有多种不同的序列,输出任意一种即可。
输入输出样例
输入
5 0 4 5 1 0 1 0 5 3 0 3 0输出
2 4
思路:
这道题是拓扑排序的模板题,所以思路主要介绍拓扑排序。
拓扑排序并不是类似于快排、冒泡给一串数字从大到小或者从小到大排序。拓扑排序的目的是:在一张有向无环图中,排出一个序列满足:图中的每一条有向边{x, y},x 在我们排出的序列中都出现在 y 之前,得到的序列我们成为拓扑序列。
为什么一定是有向无环图呢?这个问题留到后面回答。
拓扑排序的思想是:每次选中入度为0的点,删除这个点和它的出边,并把它加入拓扑序列。
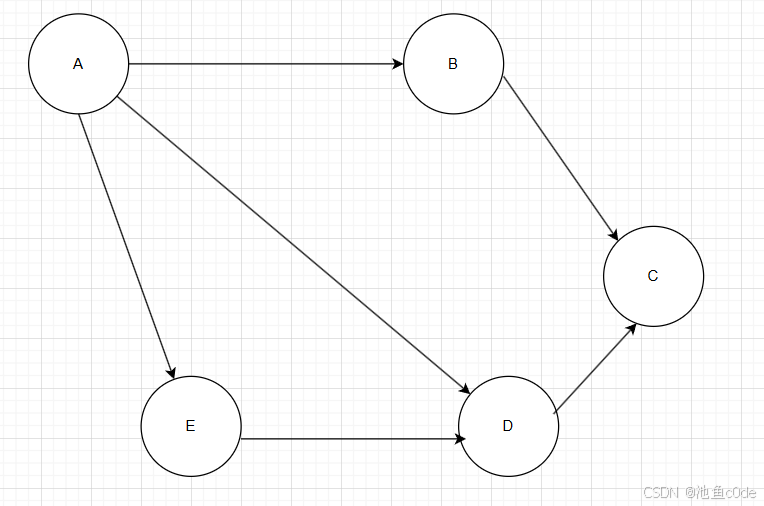
我们对这张有向无环图进行拓扑排序:
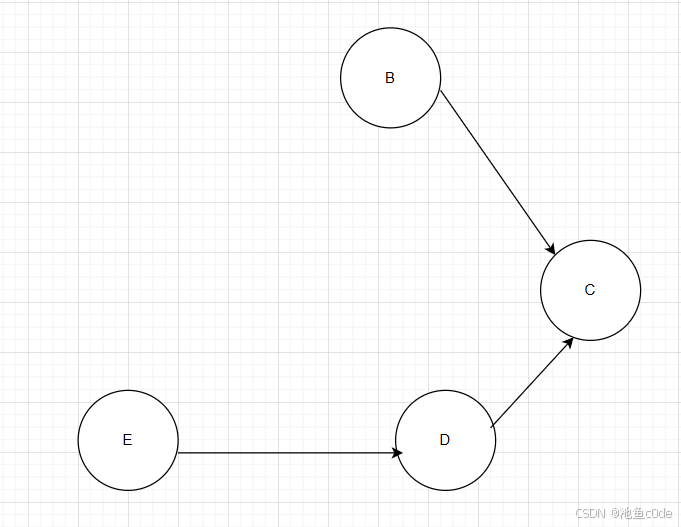
1.选中A,删除A与A的出边,把A加入拓扑序列,图片如下:
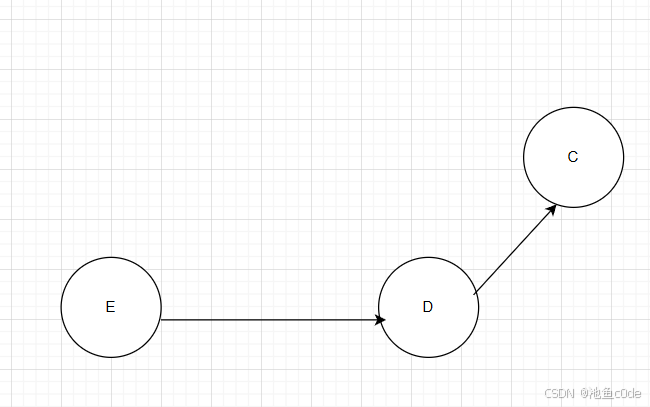
2.B和E都是入度为0的点,我们任意选一个就可以了,不难看出,拓扑序列不是唯一的,可能有多种。这里我们选B。
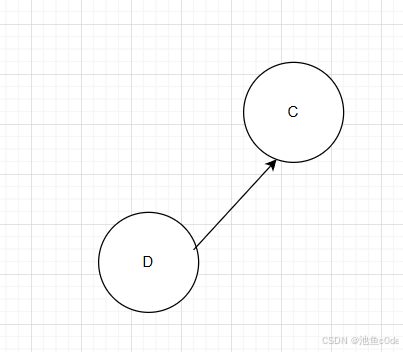
3.接下来选E,重复上述操作。当前的拓扑序列是{A,B,E}.
4.不难看出,最后得到的拓扑序列是{A,B,E,D,C}.
我们回到刚才的问题: 为什么一定是有向无环图呢?
我们以这张图为例:
接下来进行拓扑排序:
按照拓扑排序的思想,我们应该找到一个入度为0的点,而在这张图中我们找不到入度为0的点,这是因为图中出现了环。我们对它进行拓扑排序,最后得到的是一个空的拓扑序列。
根据这个特点,我们可以使用拓扑排序来判断图中是否有环,即根据最后得到的拓扑序列中元素个数是否与图中结点的个数相等。如果相等,即无环,不相等则有环。
拓扑排序的模板代码:
int h[N], e[M], nx[M], tp[N];
int idx = 0, cnt = 0;
int dx[N];
int n;
void add(int x, int y) {
e[idx] = y;
nx[idx] = h[x];
h[x] = idx;
idx++;
dx[y]++;//出度加一
}
bool topsort() {
queue<int>q;
for (int i = 1; i <= n; i++) {
if (dx[i] == 0) q.push(i);//入度为0则入队
}
while (!q.empty()) {
int x = q.front(); q.pop();
tp[cnt++] = x;
for (int i = h[x]; i != -1; i = nx[i]) {
if (--dx[e[i]] == 0) q.push(e[i]);
}
}
return cnt == n;//判断是否有环
}代码的核心思想是使用队列来维护一个入度为0的结点的集合。
其中dx[x]是结点x的入度,tp[]存放拓扑序列,使用数据模拟邻接表的方法存储图。
不了解数组模拟邻接表的可以看我上一篇博客:AcWing-1562.微博转发-再谈图的存储结构-CSDN博客
AC代码:
#include<iostream>
#include<algorithm>
#include<queue>
#include<cstring>
#define MEM(x, y) memset(x, y, sizeof x)
using namespace std;
const int N = 105, M = 1e4 + 5;
int h[N], e[M], nx[M], tp[N];
int idx = 0, cnt = 0;
int dx[N];
int n;
void add(int x, int y) {
e[idx] = y;
nx[idx] = h[x];
h[x] = idx;
idx++;
dx[y]++;
}
bool topsort() {
queue<int>q;
for (int i = 1; i <= n; i++) {
if (dx[i] == 0) q.push(i);
}
while (!q.empty()) {
int x = q.front(); q.pop();
tp[cnt++] = x;
for (int i = h[x]; i != -1; i = nx[i]) {
if (--dx[e[i]] == 0) q.push(e[i]);
}
}
return cnt == n;
}
int main() {
MEM(h, -1);
MEM(dx, 0);
cin >> n;
for (int i = 1; i <= n; i++) {
int temp = 0; cin >> temp;
while (temp != 0) {
add(i, temp);
cin >> temp;
}
}
topsort();
for (int i = 0; i < cnt; i++) {
cout << tp[i] << " ";
}
cout << endl;
return 0;
}此题还有更多更优解法,不再一一介绍了,文章尚有不足,欢迎大佬们指正。