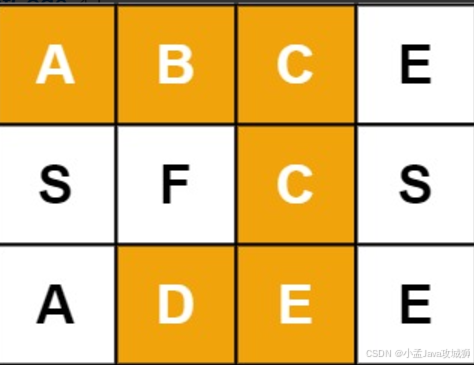
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例 1：

输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

遇到这种暴力搜索的题目就需要回溯算法出手了，因为他的下一个字母可能是四个方向的

答题模板如下

class Solution {
    public boolean exist(char[][] board, String word) {
        
    }
}

回溯三部曲想必都已经牢记于心了

第一步就是看递归函数参数和返回条件，由题目可知返回就是一个boolean值，那么可以先定义一个

boolean found = false;

看看答题模板，他给了我们一个二维board和word，这两个都要带进递归函数里面，以往我们都会用一个start来标志元素的位置，现在在二维数组里面就需要通过两个坐标来标志，参数又增加了i，j两个标志位，这时候的我已经觉得可以了但是忽然发现仅凭这些根本没办法来判断终止条件，那么如何终止呢，看了一圈条件发现，如果当长度和word的长度匹配上了不就终止了吗，这样一来，三部曲的第二个也完成了，只剩下最后的单步逻辑了，我们先写一下代码。

class Solution {
    boolean found = false;
    public boolean exist(char[][] board, String word) {
        int m = board.length, n = board[0].length;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                backtrack(board, word, 0, i, j);
            }
        }
        return found;
    }

    void backtrack(char[][] board,String word,int flag,int i,int j){
        if(flag == word.size()){
            found = true;
            return;
        }
        if(found){
            return;
        }
    }
}

本来还想简单的直接backtrack，但是发现这样的话都没有让你填入的ij，也就是都不知道你的位置，所以一开始就进行forfor循环遍历。

最后就考虑单步逻辑，既然forfor循环已经能让这个递归到每一个位置，那么在递归函数也不用在循环遍历了，只需要向不同方向递归即可，操作和撤销操作这里借鉴了一点巧思：

把char取反，加入后再返回来，就可以防止回头路了。当不相同的时候也要返回,递归的时候flag+1。

        if(word.charAt(flag)!=board[i][j]){
            return;
        }        
        board[i][j] = (char)(-board[i][j]);
        backtrack(board, word, flag + 1, i + 1, j);
        backtrack(board, word, flag + 1, i, j + 1);
        backtrack(board, word, flag + 1, i - 1, j);
        backtrack(board, word, flag + 1, i, j - 1);
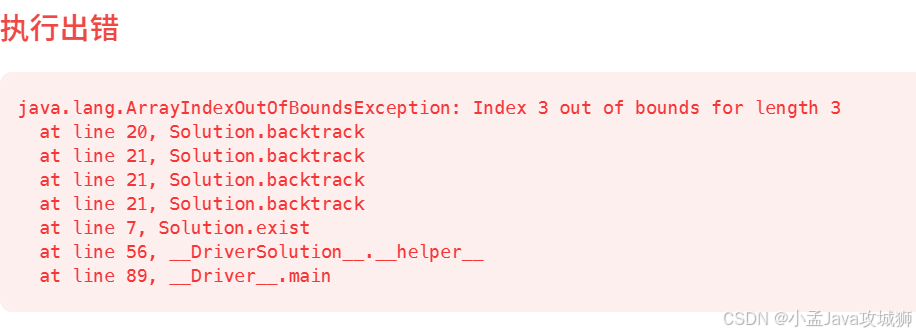
        board[i][j] = (char)(-board[i][j]);

满怀期待结果一运行就报错了，一看越界了，才想起来没做ij的判断 

 补上对ij边界的判断完整代码也就写出来了

class Solution {
    boolean found = false;

    public boolean exist(char[][] board, String word) {
        int m = board.length, n = board[0].length;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                backtrack(board, word, 0, i, j);
            }
        }
        return found;
    }

    void backtrack(char[][] board, String word, int flag, int i, int j) {
        if (flag == word.length()) {
            found = true;
            return;
        }
        if (found) {
            return;
        }
        int m = board.length, n = board[0].length;
        if (i < 0 || j < 0 || i >= m || j >= n) {
            return;
        }
        if (board[i][j] != word.charAt(flag)) {
            return;
        }

        board[i][j] = (char) (-board[i][j]);
        backtrack(board, word, flag + 1, i + 1, j);
        backtrack(board, word, flag + 1, i, j + 1);
        backtrack(board, word, flag + 1, i - 1, j);
        backtrack(board, word, flag + 1, i, j - 1);
        board[i][j] = (char) (-board[i][j]);
    }
}