凸优化学习笔记:内点法
绪论
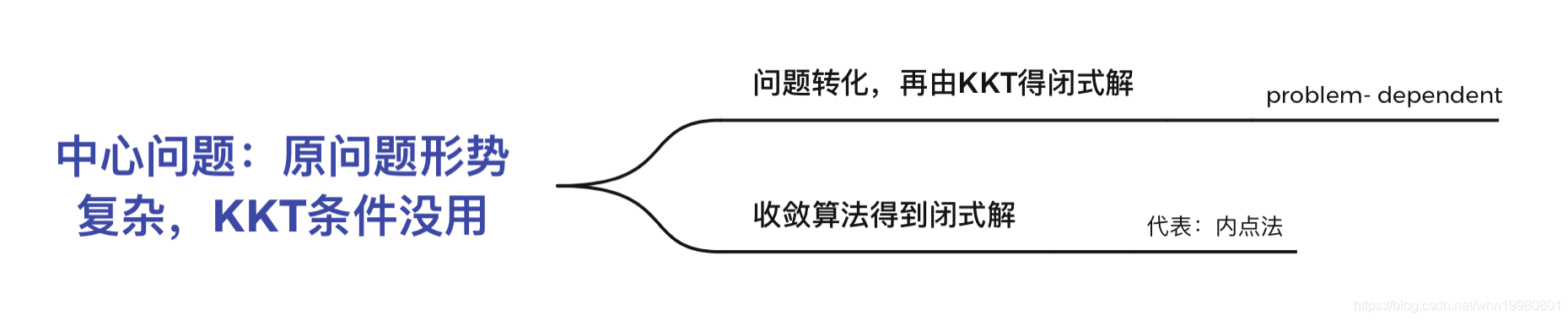
首先来讨论此处的整体逻辑:
首先拿到一个凸优化问题,KKT条件可以给我们提供最优解的一些特征,所以KKT条件有时可以直接拿到闭式解。但对于一些问题,其求导形式很复杂,KKT条件对原问题求解没有什么贡献,这是就考虑两个思路:第一、通过问题转化,得到闭式解,这个思路problem-dependent;第二、用收敛算法,代表的就是这里的内点法。
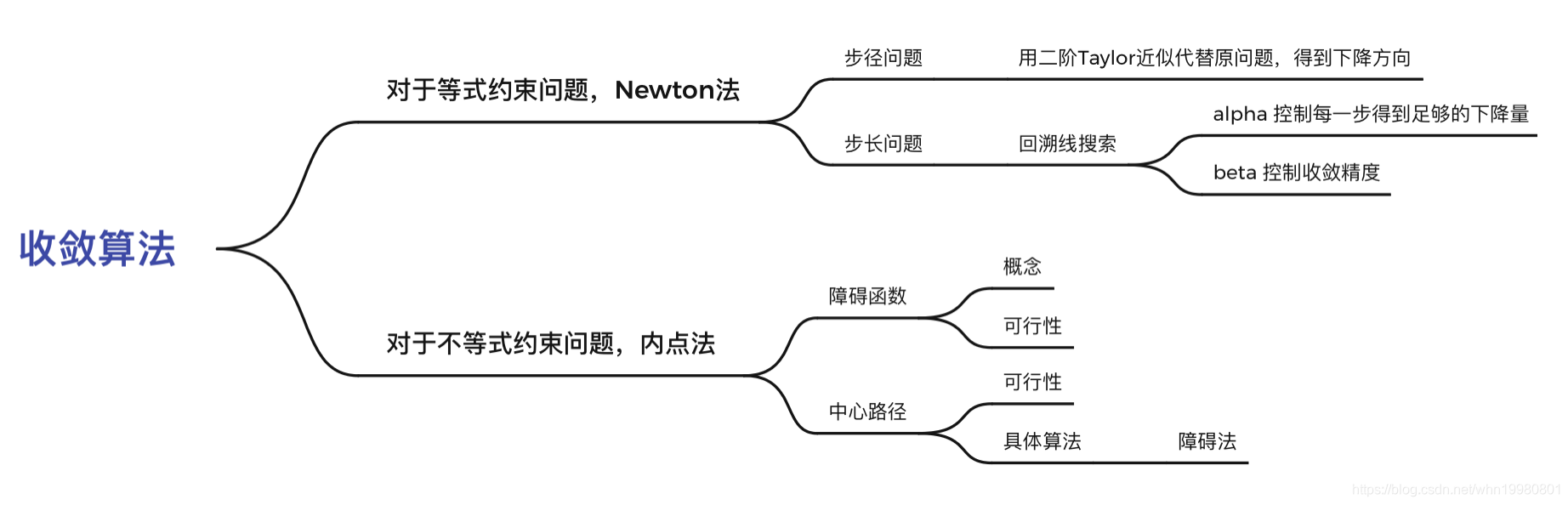
首先这里讨论等式约束问题,收敛的中心即步径和步长的确定,前者用Taylor二阶近似代替原问题给出步径方向,后者用回溯线搜索给出在一定下降量条件下的最优步长。
不等式约束问题讨论的中心是如何将其转化为一系列等式约束问题并用后者的既有算法解决。这里从Lagrange函数中将不等式约束通过指示函数写进目标函数的经验来实现。但是会产生两个问题:第一,硬限幅函数是不可微的,这表示转化之后我们没办法用凸函数的很好的性质,所以用障碍函数以一定精确度代价来代替硬限幅函数,这就是内点法的第一个主题,障碍函数。第二、用了障碍函数之后,问题就不是原来的问题了,是一个松弛之后的问题,如何有顺序的通过这一系列松弛之后的问题来得到原问题的最优解呢?这就是中心路径的问题,而中心路径即上述的“顺序”。具体概念算法可行性等等问题属于细节,此处不表。
如何解等式约束问题:Newton法
传统的等式约束问题: min f ( x ) s.t. A x = b (1) \begin{gathered} \min f(\mathbf{x}) \\ \text { s.t. } \mathbf{A x}=\mathbf{b} \end{gathered} \tag{1} minf(x) s.t. Ax=b(1)由于凸函数的良好性质:凸函数的任意一个可行点的Taylor近似都可以作为其全局下估计,基于可行点 x = x ˉ \mathbf{x}=\bar{\mathbf{x}} x=xˉ的二阶Taylor近似: f ^ ( x ) = f ( x ‾ ) + ∇ f ( x ‾ ) T ( x − x ‾ ) + 1 2 ( x − x ‾ ) T ∇ 2 f ( x ‾ ) ( x − x ‾ ) (2) \hat{f}(\mathbf{x})=f(\overline{\mathbf{x}})+\nabla f(\overline{\mathbf{x}})^{T}(\mathbf{x}-\overline{\mathbf{x}})+\frac{1}{2}(\mathbf{x}-\overline{\mathbf{x}})^{T} \nabla^{2} f(\overline{\mathbf{x}})(\mathbf{x}-\overline{\mathbf{x}}) \tag{2} f^(x)=f(x)+∇f(x)T(x−x)+21(x−x)T∇2f(x)(x−x)(2)原问题可被转化为下面的松弛之后问题: min f ^ ( x ) = f ( x ‾ ) + ∇ f ( x ‾ ) T ( x − x ‾ ) + 1 2 ( x − x ‾ ) T ∇ 2 f ( x ‾ ) ( x − x ‾ ) s.t. A x = b (3) \begin{aligned} \min & \hat{f}(\mathbf{x})=f(\overline{\mathbf{x}})+\nabla f(\overline{\mathbf{x}})^{T}(\mathbf{x}-\overline{\mathbf{x}})+\frac{1}{2}(\mathbf{x}-\overline{\mathbf{x}})^{T} \nabla^{2} f(\overline{\mathbf{x}})(\mathbf{x}-\overline{\mathbf{x}}) \\ \text { s.t. } &\mathbf{A} \mathbf{x}=\mathbf{b} \end{aligned} \tag{3} min s.t. f^(x)=f(x)+∇f(x)T(x−x)+21(x−x)T∇2f(x)(x−x)Ax=b(3)这仍然是一个凸问题,则由KKT条件: ∇ f ( x ‾ ) + ∇ 2 f ( x ‾ ) ( x − x ‾ ) + A T ν = 0 A x = b (4) \begin{aligned} \nabla f(\overline{\mathbf{x}})+\nabla^{2} f(\overline{\mathbf{x}})(\mathbf{x}-\overline{\mathbf{x}})+\mathbf{A}^{T} \boldsymbol{\nu} &=\mathbf{0} \\ \mathbf{A} \mathbf{x} &=\mathbf{b} \end{aligned} \tag{4} ∇f(x)+∇2f(x)(x−x)+ATνAx=0=b(4)矩阵化有: [ ∇ 2 f ( x ‾ ) A T A 0 ] [ x ν ] = [ ∇ 2 f ( x ‾ ) x ‾ − ∇ f ( x ‾ ) b ] (5) \left[\begin{array}{cc} \nabla^{2} f(\overline{\mathbf{x}}) & \mathbf{A}^{T} \\ \mathbf{A} & \mathbf{0} \end{array}\right]\left[\begin{array}{l} \mathbf{x} \\ \boldsymbol{\nu} \end{array}\right]=\left[\begin{array}{c} \nabla^{2} f(\overline{\mathbf{x}}) \overline{\mathbf{x}}-\nabla f(\overline{\mathbf{x}}) \\ \mathbf{b} \end{array}\right] \tag{5} [∇2f(x)AAT0][xν]=[∇2f(x)x−∇f(x)b](5)假设该问题可解,其原-对偶最优解为: [ x ⋆ ν ⋆ ] = [ ∇ 2 f ( x ‾ ) A T A 0 ] † [ ∇ 2 f ( x ‾ ) x ‾ − ∇ f ( x ‾ ) b ] + y , y ∈ N ( [ ∇ 2 f ( x ‾ ) A T A 0 ] ) (6) \left[\begin{array}{l} \mathbf{x}^{\star} \\ \boldsymbol{\nu}^{\star} \end{array}\right]=\left[\begin{array}{cc} \nabla^{2} f(\overline{\mathbf{x}}) \mathbf{A}^{T} \\ \mathbf{A} & \mathbf{0} \end{array}\right]^{\dagger}\left[\begin{array}{c} \nabla^{2} f(\overline{\mathbf{x}}) \overline{\mathbf{x}}-\nabla f(\overline{\mathbf{x}}) \\ \mathbf{b} \end{array}\right]+\mathbf{y}, \mathbf{y} \in \mathcal{N}\left(\left[\begin{array}{cc} \nabla^{2} f(\overline{\mathbf{x}}) \mathbf{A}^{T} \\ \mathbf{A} & \mathbf{0} \end{array}\right]\right) \tag{6} [x⋆ν⋆]=[∇2f(x)ATA0]†[∇2f(x)x−∇f(x)b]+y,y∈N([∇2f(x)ATA0])(6)
这里需要明确一个问题:为什么这里用Taylor二阶近似代替原函数之后再用KKT的套路,都是凸问题,原问题直接用KKT不香嘛?原因是,讨论收敛算法的背景即原问题KKT条件形式较复杂,无法实际使用时,用收敛算法。这个问题说到底是原问题形式不够友好,那我们把目标函数变成一个友好一点的函数就好了,Taylor近似是多项式函数,一般来说其本身的KKT条件式形式不难,所以有了上面逻辑。而由于Taylor近似说到底是一种近似,直接求解它作为原问题最优解是不负责任的,但是Taylor近似问题的最优解至少可以为我们提供最优解的迭代方向,这就是下面Newton法的思路。
下面为了简单起见,先去掉等式约束,则
(
6
)
(6)
(6)式退化为:
x
⋆
=
(
∇
2
f
(
x
‾
)
)
†
(
∇
2
f
(
x
‾
)
x
‾
−
∇
f
(
x
‾
)
)
+
y
~
=
x
‾
−
(
∇
2
f
(
x
‾
)
)
†
∇
f
(
x
‾
)
+
y
~
,
y
~
∈
N
(
∇
2
f
(
x
‾
)
)
(7)
\begin{aligned} \mathbf{x}^{\star} &=\left(\nabla^{2} f(\overline{\mathbf{x}})\right)^{\dagger}\left(\nabla^{2} f(\overline{\mathbf{x}}) \overline{\mathbf{x}}-\nabla f(\overline{\mathbf{x}})\right)+\tilde{\mathbf{y}} \\ &=\overline{\mathbf{x}}-\left(\nabla^{2} f(\overline{\mathbf{x}})\right)^{\dagger} \nabla f(\overline{\mathbf{x}})+\tilde{\mathbf{y}}, \tilde{\mathbf{y}} \in \mathcal{N}\left(\nabla^{2} f(\overline{\mathbf{x}})\right) \end{aligned} \tag{7}
x⋆=(∇2f(x))†(∇2f(x)x−∇f(x))+y~=x−(∇2f(x))†∇f(x)+y~,y~∈N(∇2f(x))(7)这就得到了给定可行点情况下泰勒近似式的最优解,而Newton法即以一定的步径和步长去更新可行点直至收敛至最优点:
x
‾
:
=
x
‾
+
t
⋅
d
x
‾
(8)
\overline{\mathbf{x}}:=\overline{\mathbf{x}}+t \cdot \mathbf{d}_{\overline{\mathbf{x}}} \tag{8}
x:=x+t⋅dx(8)其中步径即
d
x
‾
\mathbf{d}_{\overline{\mathbf{x}}}
dx,决定了更新的方向,步径由下式得到:
d
x
‾
=
x
⋆
−
x
‾
(9)
\mathbf{d}_{\overline{\mathbf{x}}}=\mathbf{x}^{\star}-\overline{\mathbf{x}} \tag{9}
dx=x⋆−x(9)步长由回溯线搜索得到:
这里面有两个关键:首先是判断语句
f
(
x
‾
+
t
d
x
‾
)
≤
f
(
x
‾
)
+
α
t
∇
f
(
x
‾
)
T
d
x
‾
f\left(\overline{\mathbf{x}}+t \mathbf{d}_{\overline{\mathbf{x}}}\right) \leq f(\overline{\mathbf{x}})+\alpha t \nabla f(\overline{\mathbf{x}})^{T} \mathbf{d}_{\overline{\mathbf{x}}}
f(x+tdx)≤f(x)+αt∇f(x)Tdx,说明当目前步长可以提供原函数足够的下降量时,该步长被确定,如果不能,每次更新步长时按照
t
:
=
β
t
t:=\beta t
t:=βt,
β
\beta
β越大越精确,其中
α
∈
(
0
,
0.5
)
,
β
∈
(
0
,
1
)
\alpha \in(0,0.5), \beta \in(0,1)
α∈(0,0.5),β∈(0,1)。
如何解决不等式约束问题:障碍函数以及中心路径
这里的基本逻辑是:我们上面对于等式约束问题有Newton法这种成熟的收敛算法,那么不等式约束问题该怎么处理呢?这里采用障碍函数的思想来把不等式约束问题转化为无限个等式约束问题,所以相当于是用半无限的等式约束凸问题来解决不等式约束问题。内容分为两大点:第一、障碍函数实现不等式到等式的转化思想以及可行性(障碍函数);第二、从一系列等式约束求解原来的不等式约束这种想法的可行性以及具体做法(中心路径)
障碍函数:实现不等式约束问题到等式约束问题的转化
基本思想
首先基本想法来自于Lagrange函数那里用硬限幅函数来把约束放入目标函数统一考虑的思想。首先,如果严格希望把不等式约束放入目标函数从而将不等式约束问题转化为等式约束问题,写法如下:
min
{
f
~
0
(
x
)
≜
f
0
(
x
)
+
∑
i
=
1
m
I
−
(
f
i
(
x
)
)
}
s.t.
A
x
=
b
(10)
\begin{aligned} &\min \left\{\tilde{f}_{0}(\mathbf{x}) \triangleq f_{0}(\mathbf{x})+\sum_{i=1}^{m} I_{-}\left(f_{i}(\mathbf{x})\right)\right\} \\ &\text { s.t. } \mathbf{A} \mathbf{x}=\mathbf{b} \end{aligned} \tag{10}
min{f~0(x)≜f0(x)+i=1∑mI−(fi(x))} s.t. Ax=b(10)也就是说,我们引入一个硬限幅函数
I
−
(
u
)
=
{
0
,
u
≤
0
∞
,
u
>
0
(11)
I_{-}(u)=\left\{\begin{array}{ll} 0, & u \leq 0 \\ \infty, & u>0 \end{array}\right. \tag{11}
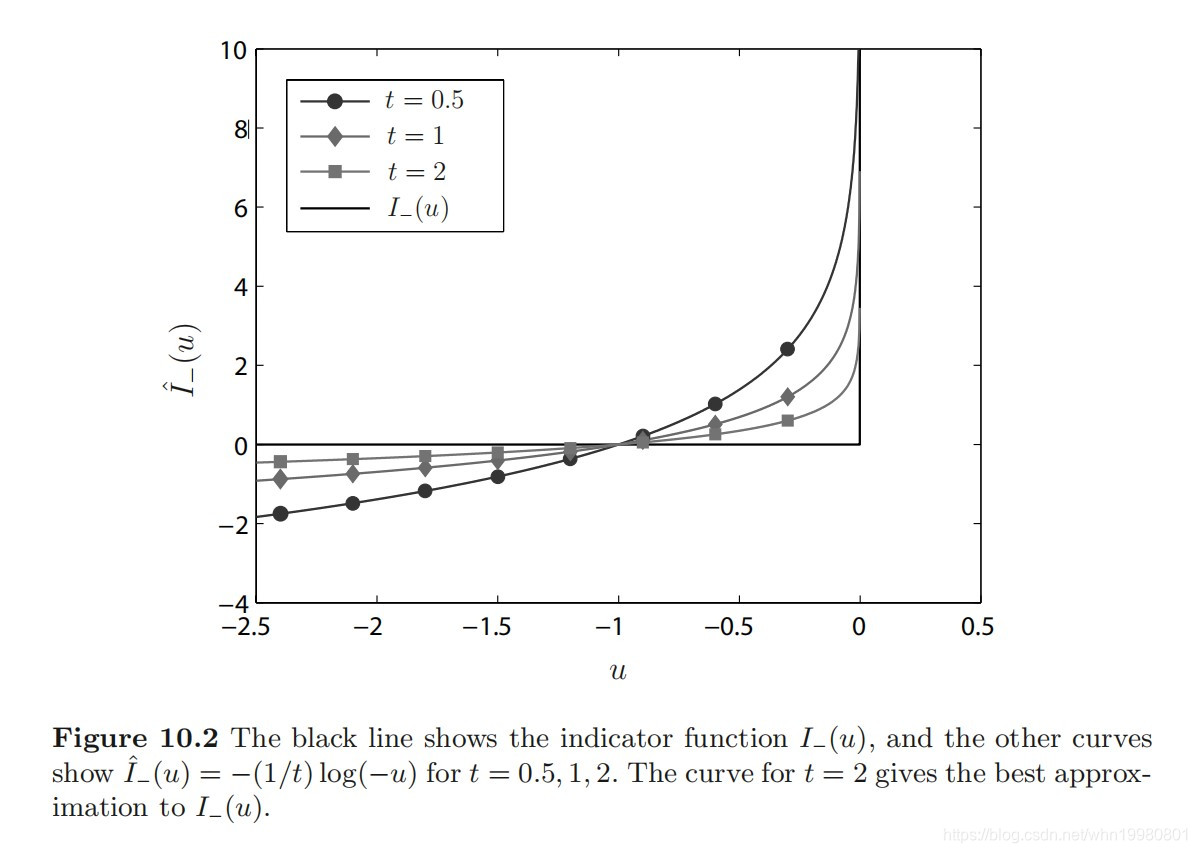
I−(u)={0,∞,u≤0u>0(11)实现问题的转化,但问题是这个硬限幅函数是不连续的,所以不可微,我们无法利用凸函数以及KKT条件那些有利的性质,这种转化对问题的求解没有贡献,所以希望用一种可微的函数来近似表示指示函数,这样做当然有代价,这里之后再讨论。这种可微的函数叫障碍函数,用对数函数作为障碍函数的方法叫做对数障碍法:
I
^
−
(
u
)
=
{
−
1
t
log
(
−
u
)
,
u
<
0
∞
,
u
≥
0
(12)
\hat{I}_{-}(u)=\left\{\begin{array}{ll} -\frac{1}{t} \log (-u), & u<0 \\ \infty, & u \geq 0 \end{array}\right. \tag{12}
I^−(u)={−t1log(−u),∞,u<0u≥0(12)对数障碍函数随
t
t
t的变化趋势如下:
引入了障碍函数之后,原始的不等式约束问题就转化为:
min
f
0
(
x
)
+
1
t
⋅
ϕ
(
x
)
s.t.
A
x
=
b
(13)
\begin{aligned} &\min f_{0}(\mathbf{x})+\frac{1}{t} \cdot \phi(\mathbf{x}) \\ &\text { s.t. } \mathbf{A x}=\mathbf{b} \end{aligned} \tag{13}
minf0(x)+t1⋅ϕ(x) s.t. Ax=b(13)其中
ϕ
(
x
)
≜
t
∑
i
=
1
m
I
^
−
(
f
i
(
x
)
)
=
−
∑
i
=
1
m
log
(
−
f
i
(
x
)
)
\phi(\mathbf{x}) \triangleq t \sum_{i=1}^{m} \hat{I}_{-}\left(f_{i}(\mathbf{x})\right)=-\sum_{i=1}^{m} \log \left(-f_{i}(\mathbf{x})\right)
ϕ(x)≜ti=1∑mI^−(fi(x))=−i=1∑mlog(−fi(x))障碍函数定义域为:
dom
ϕ
=
{
x
∈
R
n
∣
f
i
(
x
)
<
0
,
i
=
1
,
…
,
m
}
(14)
\operatorname{dom} \phi=\left\{\mathbf{x} \in \mathbb{R}^{n} \mid f_{i}(\mathbf{x})<0, i=1, \ldots, m\right\} \tag{14}
domϕ={x∈Rn∣fi(x)<0,i=1,…,m}(14)
可行性及障碍函数本质的分析
首先是一个例子
min
{
f
0
(
x
)
≜
e
−
x
+
x
3
3
}
s.t.
∣
x
∣
≤
2
(15)
\begin{aligned} &\min \left\{f_{0}(x) \triangleq e^{-x}+\frac{x^{3}}{3}\right\} \\ &\text { s.t. }|x| \leq 2 \end{aligned} \tag{15}
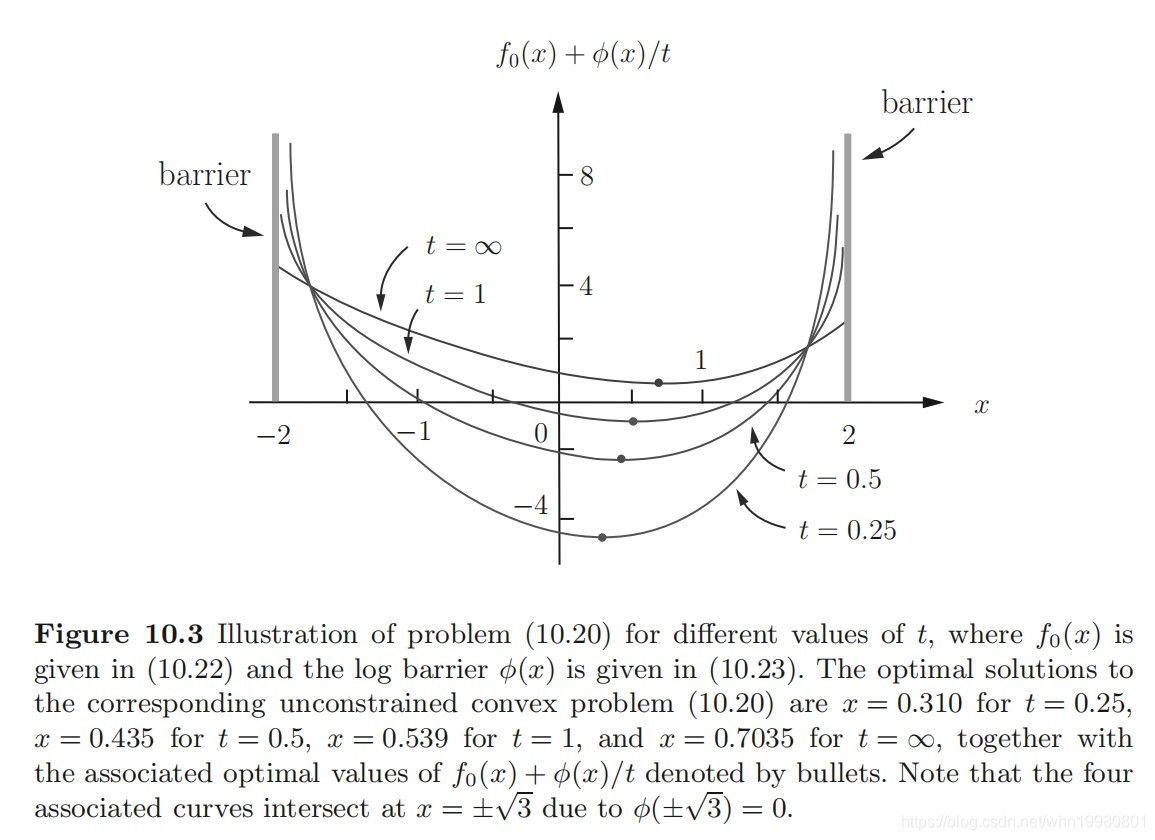
min{f0(x)≜e−x+3x3} s.t. ∣x∣≤2(15)转化后问题随
t
t
t的变化情况如下:
结合该图与上图则可以看出障碍函数是如何影响原函数的。首先 t = ∞ t=\infty t=∞对应曲线是原问题的目标函数,结合两边的barrier,其上对应的最优点是我们真实的最优点,此时由于 t t t无穷大所以障碍函数并不起实际作用。随着 t t t的减小,障碍函数作用开始越来越大,所有修正后曲线在左右两端都有公共交点,交点之内,变换平缓,交点之外,曲线陡然上升。结合上图我们知道,交点之内,障碍函数小于0,说明不等式约束成立,障碍函数会将原目标函数拉低使其原理两边边界,而交点之外,障碍函数大于0且迅速变大,原目标函数被快速拉高使得最优点不可能在两交点之外。
所以我们可以得到两个信息:
- 最优点在两交点内保证了修正后的等式约束问题的最优点对于原问题一定是可行点
- 随着 t t t的变化,最优点被左移,可以看出将不等式约束转化为等式约束,代价是精确性的下降。
所以可以看出,内点法解决不等式约束问题的本质,是利用一定程度的松弛,以牺牲一定精度为代价将不等式约束问题转化为一系列等式约束问题并用既有套路解决的过程。
障碍函数的梯度和Hessian函数为: ∇ ϕ ( x ) = ∑ i = 1 m 1 − f i ( x ) ∇ f i ( x ) ∇ 2 ϕ ( x ) = ∑ i = 1 m 1 f i 2 ( x ) ∇ f i ( x ) ∇ f i ( x ) T + ∑ i = 1 m 1 − f i ( x ) ∇ 2 f i ( x ) ⪰ 0 (16) \begin{aligned} \nabla \phi(\mathbf{x}) &=\sum_{i=1}^{m} \frac{1}{-f_{i}(\mathbf{x})} \nabla f_{i}(\mathbf{x}) \\ \nabla^{2} \phi(\mathbf{x}) &=\sum_{i=1}^{m} \frac{1}{f_{i}^{2}(\mathbf{x})} \nabla f_{i}(\mathbf{x}) \nabla f_{i}(\mathbf{x})^{T}+\sum_{i=1}^{m} \frac{1}{-f_{i}(\mathbf{x})} \nabla^{2} f_{i}(\mathbf{x}) \succeq \mathbf{0} \end{aligned} \tag{16} ∇ϕ(x)∇2ϕ(x)=i=1∑m−fi(x)1∇fi(x)=i=1∑mfi2(x)1∇fi(x)∇fi(x)T+i=1∑m−fi(x)1∇2fi(x)⪰0(16)
中心路径
基本思想以及可行性
首先是基本思想,什么是中心路径?
由上面的论断我们看到在给定的
t
t
t下,原问题被变成了一个等式约束问题并可以用Newton法求解,但这个问题不是原问题,解出来的解自然不是原问题的最优解。如果定义一个关于
t
t
t的函数
x
⋆
(
t
)
\mathbf{x}^{\star}(t)
x⋆(t),代表给定
t
t
t下问题
(
13
)
(13)
(13)的最优解,则我们更新
t
t
t走过的路径就是一个逐渐逼近真实最优解的路径,即“中心路径”。
其可行性讨论如下:
问题
(
13
)
(13)
(13)被改写为下式:
min
t
f
0
(
x
)
+
ϕ
(
x
)
s.t.
A
x
=
b
(17)
\begin{gathered} \min t f_{0}(\mathbf{x})+\phi(\mathbf{x}) \\ \text { s.t. } \mathbf{A x}=\mathbf{b} \end{gathered} \tag{17}
mintf0(x)+ϕ(x) s.t. Ax=b(17)该问题是凸问题且满足强对偶性,由KKT条件,有
ν
^
∈
R
p
\widehat{\boldsymbol{\nu}} \in \mathbb{R}^{p}
ν
∈Rp满足下式
0
=
∇
x
L
(
x
⋆
(
t
)
,
ν
^
)
=
t
∇
x
f
0
(
x
⋆
(
t
)
)
+
∇
x
ϕ
(
x
⋆
(
t
)
)
+
A
T
ν
^
=
t
∇
x
f
0
(
x
⋆
(
t
)
)
+
∑
i
=
1
m
1
−
f
i
(
x
⋆
(
t
)
)
∇
x
f
i
(
x
⋆
(
t
)
)
+
A
T
ν
^
(18)
\begin{aligned} \mathbf{0} &=\nabla_{\mathbf{x}} L\left(\mathbf{x}^{\star}(t), \widehat{\boldsymbol{\nu}}\right)=t \nabla_{\mathbf{x}} f_{0}\left(\mathbf{x}^{\star}(t)\right)+\nabla_{\mathbf{x}} \phi\left(\mathbf{x}^{\star}(t)\right)+\mathbf{A}^{T} \widehat{\boldsymbol{\nu}} \\ &=t \nabla_{\mathbf{x}} f_{0}\left(\mathbf{x}^{\star}(t)\right)+\sum_{i=1}^{m} \frac{1}{-f_{i}\left(\mathbf{x}^{\star}(t)\right)} \nabla_{\mathbf{x}} f_{i}\left(\mathbf{x}^{\star}(t)\right)+\mathbf{A}^{T} \widehat{\boldsymbol{\nu}} \end{aligned} \tag{18}
0=∇xL(x⋆(t),ν
)=t∇xf0(x⋆(t))+∇xϕ(x⋆(t))+ATν
=t∇xf0(x⋆(t))+i=1∑m−fi(x⋆(t))1∇xfi(x⋆(t))+ATν
(18)上式第一个等号是将拉格朗日函数拆开,第二个等号是把障碍函数的梯度形式拆开,我们可以看到转化后问题有着和原问题很相似的Lagrange式。
则 x ⋆ ( t ) \mathbf{x}^{\star}(t) x⋆(t)与 ν ^ ∈ R p \widehat{\boldsymbol{\nu}} \in \mathbb{R}^{p} ν ∈Rp是问题 ( 17 ) (17) (17)的原-对偶最优点,也是原问题的原-对偶可行点,对应 m / t m/t m/t次优解。
证明如下:
从上面
(
18
)
(18)
(18)式可以看出,转化后问题与原问题的Lagrange函数有如下关系:
∇
x
L
(
x
⋆
(
t
)
,
ν
^
)
/
t
=
∇
x
L
(
x
⋆
(
t
)
,
λ
⋆
(
t
)
,
ν
⋆
(
t
)
)
=
0
(19)
\nabla_{\mathbf{x}} L\left(\mathbf{x}^{\star}(t), \widehat{\boldsymbol{\nu}}\right) / t=\nabla_{\mathbf{x}} \mathcal{L}\left(\mathbf{x}^{\star}(t), \boldsymbol{\lambda}^{\star}(t), \boldsymbol{\nu}^{\star}(t)\right)=\mathbf{0} \tag{19}
∇xL(x⋆(t),ν
)/t=∇xL(x⋆(t),λ⋆(t),ν⋆(t))=0(19)那么与原问题的Lagrange式对比,我们可以看到有:
λ
i
⋆
(
t
)
=
−
1
t
f
i
(
x
⋆
(
t
)
)
≥
0
,
i
=
1
,
…
,
m
ν
⋆
(
t
)
=
ν
^
/
t
(20)
\begin{aligned} &\lambda_{i}^{\star}(t)=-\frac{1}{t f_{i}\left(\mathrm{x}^{\star}(t)\right)} \geq 0, i=1, \ldots, m \\ &\boldsymbol{\nu}^{\star}(t)=\widehat{\boldsymbol{\nu}} / t \end{aligned} \tag{20}
λi⋆(t)=−tfi(x⋆(t))1≥0,i=1,…,mν⋆(t)=ν
/t(20)利用对偶部分的理论,我们求对偶函数的极大值点:
g
(
λ
⋆
(
t
)
,
ν
⋆
(
t
)
)
=
inf
x
∈
D
L
(
x
,
λ
⋆
(
t
)
,
ν
⋆
(
t
)
)
=
L
(
x
⋆
(
t
)
,
λ
⋆
(
t
)
,
ν
⋆
(
t
)
)
=
f
0
(
x
⋆
(
t
)
)
+
∑
i
=
1
m
λ
i
⋆
(
t
)
f
i
(
x
⋆
(
t
)
)
+
ν
⋆
(
t
)
T
(
A
x
⋆
(
t
)
−
b
)
=
f
0
(
x
⋆
(
t
)
)
−
m
/
t
(21)
\begin{aligned} g\left(\boldsymbol{\lambda}^{\star}(t), \boldsymbol{\nu}^{\star}(t)\right) &=\inf _{\mathbf{x} \in \mathcal{D}} \mathcal{L}\left(\mathbf{x}, \boldsymbol{\lambda}^{\star}(t), \boldsymbol{\nu}^{\star}(t)\right)=\mathcal{L}\left(\mathbf{x}^{\star}(t), \boldsymbol{\lambda}^{\star}(t), \boldsymbol{\nu}^{\star}(t)\right) \\ &=f_{0}\left(\mathbf{x}^{\star}(t)\right)+\sum_{i=1}^{m} \lambda_{i}^{\star}(t) f_{i}\left(\mathbf{x}^{\star}(t)\right)+\boldsymbol{\nu}^{\star}(t)^{T}\left(\mathbf{A} \mathbf{x}^{\star}(t)-\mathbf{b}\right) \\ &=f_{0}\left(\mathbf{x}^{\star}(t)\right)-m / t \end{aligned} \tag{21}
g(λ⋆(t),ν⋆(t))=x∈DinfL(x,λ⋆(t),ν⋆(t))=L(x⋆(t),λ⋆(t),ν⋆(t))=f0(x⋆(t))+i=1∑mλi⋆(t)fi(x⋆(t))+ν⋆(t)T(Ax⋆(t)−b)=f0(x⋆(t))−m/t(21)
将上式解代入KKT条件有:
A
x
=
b
,
f
i
(
x
)
≤
0
,
i
=
1
,
…
,
m
λ
⪰
0
,
∇
f
0
(
x
)
+
∑
i
=
1
m
λ
i
∇
f
i
(
x
)
+
A
T
ν
=
0
,
−
λ
i
f
i
(
x
)
=
1
/
t
,
i
=
1
,
…
,
m
(22)
\begin{aligned} \mathbf{A x} &=\mathbf{b}, \\ f_{i}(\mathbf{x}) & \leq 0, i=1, \ldots, m \\ \boldsymbol{\lambda} & \succeq \mathbf{0}, \\ \nabla f_{0}(\mathbf{x})+\sum_{i=1}^{m} \lambda_{i} \nabla f_{i}(\mathbf{x})+\mathbf{A}^{T} \boldsymbol{\nu} &=\mathbf{0}, \\ -\lambda_{i} f_{i}(\mathbf{x}) &=1 / t, i=1, \ldots, m \end{aligned} \tag{22}
Axfi(x)λ∇f0(x)+i=1∑mλi∇fi(x)+ATν−λifi(x)=b,≤0,i=1,…,m⪰0,=0,=1/t,i=1,…,m(22)可以看到与传统KKT条件相比,原始的互补松弛条件不在满足,而当
t
t
t无限大时,基本满足互补松弛条件,从这里可以看出,障碍法本质上对不等式约束的松弛作用,也可以看出我们中心路径在
t
t
t趋于无穷的点即原问题的最优点。
下面是由障碍法解不等式约束问题的算法:
障碍法(连续无约束最小化技术or路径跟随法)
算法框图如下:
整体过程分外部迭代与内部迭代,外部迭代修改
t
t
t,使得等式约束问题越来越趋向不等式约束问题,即中心路径越来越趋向最优点。判决门限是目前的对偶gap是否能满足精确度
ϵ
\epsilon
ϵ;内部迭代是对于如下问题的Newton法:
min
m
ϵ
f
0
(
x
)
+
ϕ
(
x
)
s.t.
A
x
=
b
(23)
\begin{aligned} \min & \frac{m}{\epsilon} f_{0}(\mathbf{x})+\phi(\mathbf{x}) \\ \text { s.t. } & \mathbf{A x}=\mathbf{b} \end{aligned} \tag{23}
min s.t. ϵmf0(x)+ϕ(x)Ax=b(23)初始点选取只要可行即可,可以解下面的问题:
min
s
,
x
s
s.t.
f
i
(
x
)
≤
s
,
i
=
1
,
…
,
m
A
x
=
b
.
(24)
\begin{aligned} &\min _{s, \boldsymbol{x}} s \\ &\text { s.t. } f_{i}(\boldsymbol{x}) \leq s, i=1, \ldots, m \\ &\quad \mathbf{A} \boldsymbol{x}=\mathbf{b} . \end{aligned} \tag{24}
s,xmins s.t. fi(x)≤s,i=1,…,mAx=b.(24)