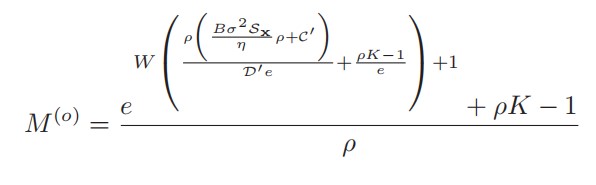本文是Emil Björnson在2015年在TWC上的一份工作：
E. Björnson, L. Sanguinetti, J. Hoydis and M. Debbah, “Optimal Design of Energy-Efficient Multi-User MIMO Systems: Is Massive MIMO the Answer?,” in IEEE Transactions on Wireless Communications, vol. 14, no. 6, pp. 3059-3075, June 2015, doi: 10.1109/TWC.2015.2400437.

总述

本文讨论在单小区多用户系统（SC-MU-MISO）中，系统的能量利用率（Energy Efficiency, EE）随基站天线数$M$、用户数$K$、发射总功率$\rho$的变化情况。相比于literature review中工作。
本文主要贡献在于：
1. 改变了以往将系统电路功耗建模为一个定值，建立了一个新的模型去描述电路功耗；
2. 基于该模型，构建了$EE$最大化问题，进而在$ZF$信号处理方法下给出了最优基站天线数$M$、用户数$K$、发射总功率$\rho$的闭式解，解释了这些参数是如何影响最终性能指标的。
3. 最后在给出了三个变量的联合优化算法，并给出了在$MRT/MRC及MMSE$信号处理方法下系统的numerical results讨论。

系统模型

信道模型

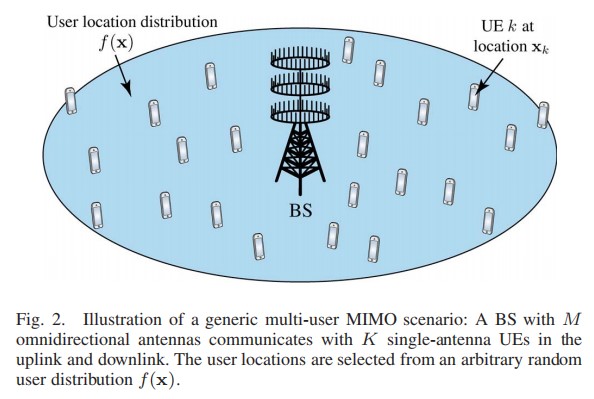
本文考虑单小区多用户系统（SC-MU-MISO），用户端单天线。系统示意图如下：

这里信道考虑大尺度衰落。具体方式是：在单小区覆盖区域中在空间上建立网格点，按照某种分布选取规定个数的用户作为每一个用户的位置，并基于位置向量给出大尺度衰落，分布与大尺度衰落如下：$$f(\mathbf{x})=\{\begin{array}{ll}\frac{1}{\pi \left(d_{\max }^2-d_{\min }^2\right)}& d_{\min }\le \Vert \mathbf{x}\Vert \le d_{\max }\\ 0& \text{ otherwise. }\end{array}\text{\hspace{1em}(1)}$$其中$\mathbf{x}$为位置向量，大尺度衰落如下式：$$l(\mathbf{x})=\frac{\bar{d}}{\Vert \mathbf{x}{\Vert }^{\kappa }}\text{ for }\Vert \mathbf{x}\Vert \ge d_{\min }\text{\hspace{1em}(2)}$$信道衰减的期望为：$${\mathbb{E}}_{\mathbf{x}}\left\{(l(\mathbf{x}){)}^{-1}\right\}=\frac{d_{\max }^{\kappa +2}-d_{\min }^{\kappa +2}}{\bar{d}\left(1+\frac{\kappa }{2}\right)\left(d_{\max }^2-d_{\min }^2\right)}\text{\hspace{1em}(3)}$$

小尺度衰落考虑传统的瑞利衰落，只考虑NLOS径，则最终的信道向量建模如下，对第$k$个用户：$${\mathbf{h}}_k\sim \mathcal{C}\mathcal{N}\left(0_M,l\left({\mathbf{x}}_k\right){\mathbf{I}}_M\right)$$其中${\mathbf{h}}_k={\left[h_{k,1},h_{k,2},\dots ,h_{k,M}\right]}^T\in {\mathbb{C}}^{M\times 1}$，$M$为基站端天线个数。

传输模型

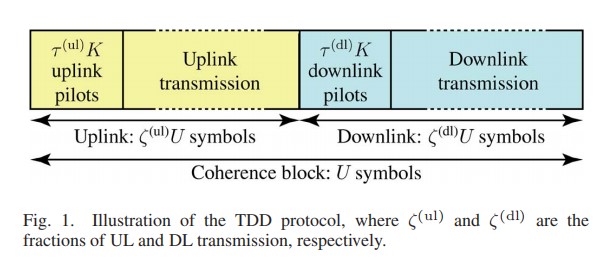
此处考虑上下行传输，采用TDD架构，帧结构如下：

这里$U=B_c{T}_c$代表信道可用总资源，其中$B_c$为相干带宽，$T_c$代表相干时间。用${\zeta }^{(\mathrm{u}\mathrm{l})}+{\zeta }^{(\mathrm{d}\mathrm{l})}=1$表示上行信道和下行信道所占总资源的比例，在每一段传输中，用${\tau }^{(\text{dl})}K$和${\tau }^{(\text{ul})}K$表征导频所占的时间资源。

信号处理过程

上行和下行信号处理均在基站端实现，上行为MIMO detection，下行为MIMO precoding。信号处理矩阵用$\mathbf{G}=\left[{\mathbf{g}}_1,{\mathbf{g}}_2,\dots ,{\mathbf{g}}_K\right]\in {\mathbb{C}}^{M\times K}$表示，对上行detection：$$\mathbf{G}=\{\begin{array}{ll}\mathbf{H}& \text{ for MRC, }\\ \mathbf{H}{\left({\mathbf{H}}^H\mathbf{H}\right)}^{-1}& \text{ for }\mathrm{Z}\mathrm{F},\\ {\left({\mathbf{H}\mathbf{P}}^{(\mathrm{u}\mathrm{l})}{\mathbf{H}}^H+{\sigma }^2{\mathbf{I}}_M\right)}^{-1}\mathbf{H}& \text{ for MMSE }\end{array}\text{\hspace{1em}(4)}$$对下行precoding：$$\mathbf{V}=\{\begin{array}{ll}\mathbf{H}& \text{ for MRT, }\\ \mathbf{H}{\left({\mathbf{H}}^H\mathbf{H}\right)}^{-1}& \text{ for ZF, }\\ {\left({\mathbf{H}\mathbf{P}}^{(\mathrm{u}\mathrm{l})}{\mathbf{H}}^H+{\sigma }^2{\mathbf{I}}_M\right)}^{-1}\mathbf{H}& \text{ for MMSE. }\end{array}\text{\hspace{1em}(5)}$$

上下行传输 速率及功率分配

本文目标是使得所有用户能有统一的总速率$\bar{R}$（即无偏好服务）。

上行信道

因为传输中要分出一部分资源用来传输导频，上行信道实际信息速率为：$$R_k^{(\mathrm{u}\mathrm{l})}={\zeta }^{(\mathrm{u}\mathrm{l})}\left(1-\frac{{\tau }^{(\mathrm{u}\mathrm{l})}K}{U{\zeta }^{(\mathrm{u}\mathrm{l})}}\right){\bar{R}}_k^{(\mathrm{u}\mathrm{l})}\text{\hspace{1em}(6)}$$第$k$个用户上行和速率为：$${\bar{R}}_k^{(\mathrm{u}\mathrm{l})}=B\log \left(1+\frac{p_k^{(\mathrm{u}\mathrm{l})}{\left|{\mathbf{g}}_k^H{\mathbf{h}}_k\right|}^2}{{\sum }_{\ell =1,\ell \ne k}^K{p}_{\ell }^{(\mathrm{u}\mathrm{l})}{\left|{\mathbf{g}}_k^H{\mathbf{h}}_{\ell }\right|}^2+{\sigma }^2{\Vert {\mathbf{g}}_k\Vert }^2}\right)\text{\hspace{1em}(7)}$$本文设计目标希望通过power allocation使得各个用户的和速率相同，根据参考文献，此时功率分配向量${\mathbf{p}}^{(\mathrm{u}\mathrm{l})}={\left[p_1^{(\mathrm{u}\mathrm{l})},p_2^{(\mathrm{u}\mathrm{l})},\dots ,p_K^{(\mathrm{u}\mathrm{l})}\right]}^T$有如下闭式解：$${\mathbf{p}}^{(\mathrm{u}\mathrm{l})}={\sigma }^2{\left({\mathbf{D}}^{(\mathrm{u}\mathrm{l})}\right)}^{-1}{1}_K\text{\hspace{1em}(8)}$$${\mathbf{D}}^{(\mathrm{u}\mathrm{l})}\in {\mathbb{C}}^{K\times K}$的$(k,l)$项有：$${\left[{\mathbf{D}}^{(\mathrm{u}\mathrm{l})}\right]}_{k,\ell }=\{\begin{array}{ll}\frac{{|{\mathbf{g}}_k^H{\mathbf{h}}_k|}^2}{\left(2^{\bar{R}/B}-1\right){\Vert {\mathbf{g}}_k\Vert }^2}& \text{ for }k=\ell ,\\ -\frac{{|{\mathbf{g}}_k^H{\mathbf{h}}_{\ell }|}^2}{{\Vert {\mathbf{g}}_k\Vert }^2}& \text{ for }k\ne \ell .\end{array}\text{\hspace{1em}(9)}$$基于此，上行传输的PA（功放）平均耗散为：$$\begin{array}{rl}{P}_{\mathrm{T}\mathrm{X}}^{(\mathrm{u}\mathrm{l})}& =\frac{B{\zeta }^{(\mathrm{u}\mathrm{l})}}{{\eta }^{(\mathrm{u}\mathrm{l})}}\mathbb{E}\left\{1_K^T{\mathbf{p}}^{(\mathrm{u}\mathrm{l})}\right\}\\ & ={\sigma }^2\frac{B{\zeta }^{(\mathrm{u}\mathrm{l})}}{{\eta }^{(\mathrm{u}\mathrm{l})}}\mathbb{E}\left\{1_K^T{\left({\mathbf{D}}^{(\mathrm{u}\mathrm{l})}\right)}^{-1}{1}_K\right\}\end{array}\text{\hspace{1em}(10)}$$其中$0<{\eta }^{(\mathrm{u}\mathrm{l})}\le 1$是用户端的PA效率。
对于$ZF$信号处理，有结论：$$\bar{R}=B\log (1+\rho (M-K))\text{\hspace{1em}(11)}$$其中$\rho$与接收信噪比成正比。PA功率为：$$P_{\mathrm{T}\mathrm{X}}^{(\mathrm{u}\mathrm{l}-\mathrm{Z}\mathrm{F})}=\frac{B{\zeta }^{(\mathrm{u}\mathrm{l})}}{{\eta }^{(\mathrm{u}\mathrm{l})}}{\sigma }^2\rho {\mathcal{S}}_{\mathbf{x}}K\text{\hspace{1em}(12)}$$其中${\mathcal{S}}_{\mathbf{x}}={\mathbb{E}}_{\mathbf{x}}\left\{(l(\mathbf{x}){)}^{-1}\right\}$是路损的期望。

下行信道

下行信道分析同上行信道，首先第$k$个用户的可行速率为：$$R_k^{(\mathrm{d}\mathrm{l})}={\zeta }^{(\mathrm{d}l)}\left(1-\frac{{\tau }^{(\mathrm{d}\mathrm{l})}K}{U{\zeta }^{(\mathrm{d}l)}}\right){\bar{R}}_k^{(\mathrm{d}\mathrm{l})}\text{\hspace{1em}(13)}$$其中总速率为$${\bar{R}}_k^{(\mathrm{d}\mathrm{l})}=B\log \left(1+\frac{p_k^{(\mathrm{d}\mathrm{l})}\frac{{|{\mathbf{h}}_k^H{\mathbf{v}}_k|}^2}{{\Vert {\mathbf{v}}_k\Vert }^2}}{{\sum }_{\ell =1,\ell \ne k}^K{p}_{\ell }^{(\mathrm{d}1)}\frac{{|{\mathbf{h}}_k^H{\mathbf{v}}_{\ell }|}^2}{{\Vert {\mathbf{v}}_{\ell }\Vert }^2}+{\sigma }^2}\right)\text{\hspace{1em}(14)}$$平均PA功率$$P_{\mathrm{T}\mathrm{X}}^{(\mathrm{d}1)}=\frac{B{\zeta }^{(\mathrm{d}\mathrm{l})}}{{\eta }^{(\mathrm{d}l)}}\sum _{k=1}^K\mathbb{E}\left\{p_k^{(\mathrm{d}\mathrm{l})}\right\}\text{\hspace{1em}(15)}$$保证用户总速率统一的功率分配方案同上行信道，其中下行功率分配向量为：${\mathbf{p}}^{(\mathrm{d}\mathrm{l})}={\sigma }^2{\left({\mathbf{D}}^{(\mathrm{d}\mathrm{l})}\right)}^{-1}{1}_K$，其中${\mathbf{D}}^{(\mathrm{d}\mathrm{l})}\in {\mathbb{C}}^{K\times K}$的$(k,l)$项有：$${\left[{\mathbf{D}}^{(\mathrm{d}\mathrm{l})}\right]}_{k,\ell }=\{\begin{array}{ll}\frac{{|{\mathbf{h}}_k^H{\mathbf{v}}_k|}^2}{\left(2^{\bar{R}/B}-1\right){\Vert {\mathbf{v}}_k\Vert }^2}& \text{ for }k=\ell ,\\ -\frac{{|{\mathbf{h}}_k^H{\mathbf{v}}_{\ell }|}^2}{{\Vert {\mathbf{v}}_{\ell }\Vert }^2}& \text{ for }k\ne \ell .\end{array}\text{\hspace{1em}(16)}$$代入上面式$(15)$，下行PA功耗为：$$P_{\mathrm{T}\mathrm{X}}^{(\mathrm{d}\mathrm{l})}={\sigma }^2\frac{B{\zeta }^{(\mathrm{d}\mathrm{l})}}{{\eta }^{(\mathrm{d}\mathrm{l})}}\mathbb{E}\left\{1_K^T{\left({\mathbf{D}}^{(\mathrm{d}\mathrm{l})}\right)}^{-1}{1}_K\right\}\text{\hspace{1em}(17)}$$若上下行信号处理方式相同，则上下行传输总PA功耗相同，而同一用户上下行传输分配功率不同。后面给出了ZF预编码在下行信道中结论，详情见论文，此处不赘述。

问题构建

首先能量利用率的定义是每一焦耳能量所能传输的bit数，则上下行EE定义如下：$$\mathrm{E}\mathrm{E}=\frac{{\sum }_{k=1}^K\left(\mathbb{E}\left\{R_k^{(\mathrm{u}\mathrm{l})}\right\}+\mathbb{E}\left\{R_k^{(\mathrm{d}\mathrm{l})}\right\}\right)}{P_{\mathrm{T}\mathrm{X}}^{(\mathrm{u}\mathrm{l})}+P_{\mathrm{T}\mathrm{X}}^{(\mathrm{d}\mathrm{l})}+P_{\mathrm{C}\mathrm{P}}}\text{\hspace{1em}(18)}$$其中$P_{\mathrm{C}\mathrm{P}}$为电路功耗。
传统工作中将$P_{\mathrm{C}\mathrm{P}}$当定值，本文进一步分析了电路功耗的组成部分，将其定义为发端天线数，用户数，以及发射功率的函数，则EE定义式如下：$$\underset{M\in {\mathbb{Z}}_{+},K\in {\mathbb{Z}}_{+},\bar{R}\ge 0}{\mathrm{EE}}=\frac{{\sum }_{k=1}^K\left(\mathbb{E}\left\{R_k^{(\mathrm{u}\mathrm{l})}\right\}+\mathbb{E}\left\{R_k^{(\mathrm{d}\mathrm{l})}\right\}\right)}{P_{\mathrm{T}\mathrm{X}}^{(\mathrm{u}\mathrm{l})}+P_{\mathrm{T}\mathrm{X}}^{(\mathrm{d}\mathrm{I})}+P_{\mathrm{C}\mathrm{P}}(M,K,\bar{R})}\text{\hspace{1em}(19)}$$
经过之前对于速率以及上下行PA功率闭式解的推导，EE闭式中到此只有$P_{CP}$未知，传统工作将$P_{CP}$直接当常数处理，本文的贡献则是利用电路原理将其拆分，形成关于自变量的函数，构建新的优化问题进行分析。

电路功耗模型分析

电路功耗的组成部分：$$P_{\mathrm{C}\mathrm{P}}=P_{\mathrm{F}\mathrm{I}\mathrm{X}}+P_{\mathrm{T}\mathrm{C}}+P_{\mathrm{C}\mathrm{E}}+P_{\mathrm{C}/\mathrm{D}}+P_{\mathrm{B}\mathrm{H}}+P_{\mathrm{L}\mathrm{P}}\text{\hspace{1em}(20)}$$其中$P_{\mathrm{F}\mathrm{I}\mathrm{X}}$为功率中不变量，$P_{\mathrm{T}\mathrm{C}}$为收发链路功耗，$P_{\mathrm{C}\mathrm{E}}$为信道估计过程中功耗，$P_{\mathrm{C}/\mathrm{D}}$为信道编码及解码过程功耗，$P_{\mathrm{B}\mathrm{H}}$为负载回程功耗，是基站与中心核网络进行信息交互时的功耗，$P_{\mathrm{L}\mathrm{P}}$是基站端进行线性信号处理时的功耗。
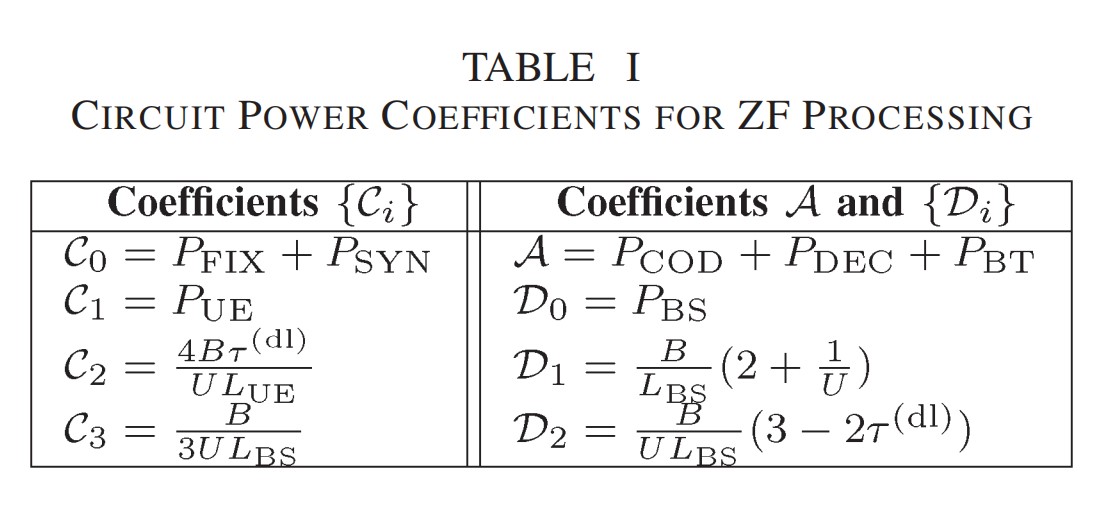
各部分功耗现归纳如下，只展示结论，具体见原论文：
$$P_{\mathrm{T}\mathrm{C}}=M{P}_{\mathrm{B}\mathrm{S}}+P_{\mathrm{S}\mathrm{Y}\mathrm{N}}+K{P}_{\mathrm{U}\mathrm{E}}\text{ Watt }\text{\hspace{1em}(21)}$$$$P_{\mathrm{C}\mathrm{E}}=\frac{B}{U}\frac{2{\tau }^{(\mathrm{u}\mathrm{l})}M{K}^2}{L_{\mathrm{B}\mathrm{S}}}+\frac{B}{U}\frac{4{\tau }^{(\mathrm{d}\mathrm{l})}{K}^2}{L_{\mathrm{U}\mathrm{E}}}\text{ Watt. }\text{\hspace{1em}(22)}$$前者是上行信道估计时功耗。其中$B$为带宽，$\frac{B}{U}$为每秒钟对应的带宽，$L_{\mathrm{B}\mathrm{S}}$与$L_{\mathrm{U}\mathrm{E}}$为基站及用户端的运算效率。整体的物理含义为信道估计所需做的计算量除以计算效率。$$P_{\mathrm{C}/\mathrm{D}}=\sum _{k=1}^K\left(\mathbb{E}\left\{R_k^{(\mathrm{u}\mathrm{l})}+R_k^{(\mathrm{d}\mathrm{l})}\right\}\right)\left(P_{\mathrm{C}\mathrm{O}\mathrm{D}}+P_{\mathrm{D}\mathrm{E}\mathrm{C}}\right)\text{ Watt }\text{\hspace{1em}(23)}$$对于给定的信号处理算法来说，可认为是定值。$$P_{\mathrm{B}\mathrm{H}}=\sum _{k=1}^K\left(\mathbb{E}\left\{R_k^{(\mathrm{u}\mathrm{l})}+R_k^{(\mathrm{d}\mathrm{l})}\right\}\right)P_{\mathrm{B}\mathrm{T}}\text{ Watt }\text{\hspace{1em}(24)}$$$$P_{\mathrm{L}\mathrm{P}}=B\left(1-\frac{\left({\tau }^{(\mathrm{u}\mathrm{l})}+{\tau }^{(\mathrm{d}\mathrm{l})}\right)K}{U}\right)\frac{2MK}{L_{\mathrm{B}\mathrm{S}}}+P_{\mathrm{L}\mathrm{P}-\mathrm{C}}\text{ Watt }\text{\hspace{1em}(25)}$$后一段与具体算法有关，而本文讨论的算法功耗如下：$$P_{\mathrm{L}\mathrm{P}-\mathrm{C}}^{(\mathrm{M}\mathrm{R}\mathrm{T}/\mathrm{M}\mathrm{R}\mathrm{C})}=\frac{B}{U}\frac{3MK}{L_{\mathrm{B}\mathrm{S}}}\text{ Watt }\text{\hspace{1em}(26)}$$$$P_{\mathrm{L}\mathrm{P}-\mathrm{C}}^{(\mathrm{Z}\mathrm{F})}=\frac{B}{U}\left(\frac{K^3}{3L_{\mathrm{B}\mathrm{S}}}+\frac{3M{K}^2+MK}{L_{\mathrm{B}\mathrm{S}}}\right)\text{ Watt }\text{\hspace{1em}(27)}$$MMSE信号处理算法需要定点迭代，这里固定其迭代次数为$Q$次，则MMSE功耗为：$$P_{\mathrm{L}\mathrm{P}-\mathrm{C}}^{(\mathrm{M}\mathrm{M}\mathrm{S}\mathrm{E})}=Q{P}_{\mathrm{L}\mathrm{P}-\mathrm{C}}^{(\mathrm{Z}\mathrm{F})}\text{\hspace{1em}(28)}$$

EE优化问题求解（ZF）

到这里为止，文章的贡献已经出来了，即一改之间将电路功耗常数化的建模方式，并基于此构建新的优化问题。上面解决了电路功耗如何描述的问题，下面解决的就是如何解的问题。

下面分：问题构建；整体求解的框架，交替最小化；定二求一。

问题构建

在ZF信号处理方式下，EE问题降级为：$${\mathrm{maximize}}_{\genfrac{}{}{0ex}{}{M\in {\mathbb{Z}}_{+},K\in {\mathbb{Z}}_{+},\rho \ge 0}{M\ge K+1}}{\mathrm{E}\mathrm{E}}^{(\mathrm{Z}\mathrm{F})}=\frac{K\left(1-\frac{{\tau }_{\mathrm{s}\mathrm{u}\mathrm{m}}K}{U}\right)\bar{R}}{\frac{B{\sigma }^2\rho {\mathcal{S}}_{\mathrm{x}}}{\eta }K+P_{\mathrm{C}\mathrm{P}}^{(\mathrm{Z}\mathrm{F})}}\text{\hspace{1em}(29)}$$其中${\tau }_{\mathrm{r}\mathrm{m}}$为单位导频估计所占总时长$${\tau }_{\text{sum }}={\tau }^{(\mathrm{u}\mathrm{l})}+{\tau }^{(\mathrm{d}l)}\text{\hspace{1em}(30)}$$将上述功耗分析代入有：$$P_{\mathrm{C}\mathrm{P}}^{(\mathrm{Z}\mathrm{F})}=\sum _{i=0}^3{\mathcal{C}}_i{K}^i+M\sum _{i=0}^2{\mathcal{D}}_i{K}^i+\mathcal{A}K\left(1-\frac{{\tau }_{\mathrm{s}\mathrm{u}\mathrm{m}}K}{U}\right)\bar{R}\text{\hspace{1em}(31)}$$EE目标函数为：$$\begin{array}{rl}& {\mathrm{E}\mathrm{E}}^{(\mathrm{Z}\mathrm{F})}\\ & =\frac{K\left(1-\frac{{\tau }_{\mathrm{s}\mathrm{u}\mathrm{m}}K}{U}\right)\bar{R}}{\frac{B{\sigma }^2\rho S_{\mathrm{x}}}{\eta }K+{\sum }_{i=0}^3{\mathcal{C}}_i{K}^i+M{\sum }_{i=0}^2{\mathcal{D}}_i{K}^i+\mathcal{A}K\left(1-\frac{{\tau }_{\text{sum }}}{U}\right)\bar{R}}\end{array}\text{\hspace{1em}(32)}$$该式看似复杂，实际是将上述所有结论的参数化，参数总结如下：

整体求解的框架（交替优化）

问题构建出来了，怎么解呢，文章采用了交替优化的方式：

单个优化变量怎么解（定二求一）

最优用户数

闭式解

当基站天线数与发射总功率为定值时，最优用户数为：$$K^{\star }=\underset{\ell }{\max }\lfloor K_{\ell }^{(o)}\rceil \text{\hspace{1em}(33)}$$其中$K_{\ell }^{(o)}$为下面四次方程正实根：$$K^4-\frac{2U}{{\tau }_{\text{sum }}}{K}^3-{\mu }_1{K}^2-2{\mu }_{0}K+\frac{U{\mu }_0}{{\tau }_{\text{sum }}}=0\text{\hspace{1em}(34)}$$其中${\mu }_1=\frac{\frac{U}{{\tau }_{\text{sum }}}\left({\mathcal{C}}_2+\bar{\beta }{\mathcal{D}}_1\right)+{\mathcal{C}}_1+\bar{\beta }{\mathcal{D}}_0}{{\mathcal{C}}_3+\bar{\beta }{\mathcal{D}}_2}$ ${\mu }_0=\frac{{\mathcal{C}}_0+\frac{B{\sigma }^2{\mathcal{S}}_{\mathbf{x}}}{\eta }\bar{\rho }}{{\mathcal{C}}_3+\bar{\beta }{\mathcal{D}}_2}$
上述方程最大正实根有闭式解，也有高效的数值逼近算法可解。

结论

下面从该结果研究最佳用户数的变化规律，下面直接给出结论：

1. $K^{\star }$与单用户或单基站天线所分功率成反比；
2. 与电路功耗成正比，尤其是其中$P_{FIX}$与$P_{SYN}$
3. 与电路中其他功耗无关，如：$P_{COD},P_{DEC},P_{BT}$
4. 当基站覆盖范围较大时，应服务尽量多用户

最优BS天线数

闭式解

$M^{\star }=\lfloor M^{(o)}\rceil$，其中

${\mathcal{C}}^{\prime }=\frac{{\sum }_{i=0}^3{\mathcal{C}}_i{K}^i}{K}\text{ and }{\mathcal{D}}^{\prime }=\frac{{\sum }_{i=0}^2{\mathcal{D}}_i{K}^i}{K}$

结论

1. $M^{\star }$与$P_{COD},P_{DEC},P_{BT}$无关
2. 与BS单天线分配功率$P_{BS}$成反比
3. 与$P_{FIX},P_{SYN},P_{UE}$成正比
4. 最优BS天线数下限$M^{\star }\ge K+\frac{\frac{B{\sigma }^2{\mathcal{S}}_{\mathbf{x}}}{\eta {\mathcal{D}}^{\prime }}\rho +\frac{{\mathcal{C}}^{\prime }}{{\mathcal{D}}^{\prime }}+K-\frac{1}{\rho }}{\ln (\rho )+\ln \left(\frac{B{\sigma }^2{\mathcal{S}}_{\mathbf{x}}}{\eta {\mathcal{D}}^{\prime }}\rho +\frac{{\mathcal{C}}^{\prime }}{{\mathcal{D}}^{\prime }}+K-\frac{1}{\rho }\right)-1}-\frac{1}{\rho }$
5. 发端功率较大时，有近似式：$M^{\star }\approx \frac{B{\sigma }^2{\mathcal{S}}_{\mathbf{x}}}{2\eta {\mathcal{D}}^{\prime }}\frac{\rho }{\ln (\rho )}$
6. 基站覆盖区域变大时，随配天线数也应增大

最优发射功率

闭式解

$${\rho }^{\star }=\frac{e^{W\left(\frac{\eta }{B{\sigma }^2{\mathcal{S}}_{\mathbf{x}}}\frac{(M-K)\left({\mathcal{C}}^{\prime }+M{\mathcal{D}}^{\prime }\right)}{e}-\frac{1}{e}\right)+1}-1}{M-K}\text{\hspace{1em}(35)}$$其中${\mathcal{C}}^{\prime }=\frac{{\sum }_{i=0}^3{\mathcal{C}}_i{K}^i}{K}\text{ and }{\mathcal{D}}^{\prime }=\frac{{\sum }_{i=0}^2{\mathcal{D}}_i{K}^i}{K}$且都大于0。

结论

1. 最佳发射功率与$P_{COD},P_{DEC},P_{BT}$无关
2. 下限：$${\rho }^{\star }\ge \frac{\frac{\eta \left({\mathcal{C}}^{\prime }+M{\mathcal{D}}^{\prime }\right)}{B{\sigma }^2{\mathcal{S}}_{\mathbf{x}}}-\frac{\ln \left(\frac{\eta (M-K)\left({\mathcal{C}}^{\prime }+M{\mathcal{D}}^{\prime }\right)}{B{\sigma }^2{\mathcal{S}}_{\mathbf{x}}}-1\right)}{(M-K)}}{\ln \left(\frac{\eta (M-K)\left({\mathcal{C}}^{\prime }+M{\mathcal{D}}^{\prime }\right)}{B{\sigma }^2{\mathcal{S}}_{\mathbf{x}}}-1\right)-1}$$
3. massive MIMO 下近似解：$${\rho }^{\star }\approx \frac{\eta {\mathcal{D}}^{\prime }}{2B{\sigma }^2{\mathcal{S}}_{\mathbf{x}}}\frac{M}{\ln (M)}$$