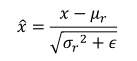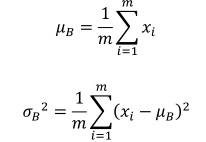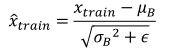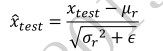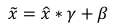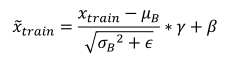学习记录：

  深度学习笔记（一）：卷积层+激活函数+池化层+全连接层
  深度学习笔记（二）：激活函数总结
  深度学习笔记（三）：BatchNorm（BN）层
  深度学习笔记（四）：梯度下降法与局部最优解
  深度学习笔记（五）：欠拟合、过拟合

   防止过拟合（一）：正则化
   防止过拟合（二）：Dropout
   防止过拟合（三）：数据增强

一、背景

  卷积神经网络的出现，网络参数量大大减低，使得几十层的深层网络成为可能。然而，在残差网络出现之前，网络的加深使得网络训练变得非常不稳定，甚至出现网络长时间不更新或者不收敛的情形，同时网络对超参数比较敏感，超参数的微量扰动也会导致网络的训练轨迹完全改变。

二、提出

  2015 年，Google 研究人员Sergey Ioffe等提出了一种参数标准化(Normalize)的手段，并基于参数标准化设计了 Batch Nomalization(简称 BatchNorm或 BN)层 。BN层提出后：
（1）使得网络的超参数的设定更加自由，比如更大的学习率，更随意的网络初始化等，同时网络的收敛速度更快，性能也更好。
（2）广泛地应用在各种深度网络模型上，卷积层、BN 层，ReLU 层、池化层一度成为网络模型的标配单元，通过堆叠 Conv-BN-ReLU-Pooling 方式往往可以获得不错的模型性能。

三、原理

  网络层的输入x分布相近，并且分布在较小范围内时(如 0 附近)，更有利于函数的迭代优化。那么如何保证输入x的分布相近呢？
数据标准化可以实现此目的，通过数据标准化操作可以将数据x映射$\hat{x}$：

  其中${\mu }_r$、${\delta }_r^2$来自统计的所有数据x的均值和方差，$ϵ$是为防止出现除 0的错误而设置的较小数，比如$ϵ=1e-8$。
  很容易很看出来：上面的公式表示的是正太分布。也就是说，通过上面的公式计算，可以将原本随机分布的输入数据x，转化成按正太分布分布的数据$\hat{x}$，从而使得输入网络的数据分布较近，有利于网络的迭代优化。

四、计算

  要使得原本的输入x映射到正太分布的$\hat{x}$，就需要分别计算出${\mu }_r$和${\delta }_r^2$的值，然后带入下面公式，完成转换。
（1）训练阶段
  通过统计可以得到Batch组数据的均值${\mu }_B$和方差${\delta }_B^2$，计算公式如下：

  其中，m为Batch样本数。在实际应用过程中，${\mu }_B$、${\delta }_B^2$近似于${\mu }_r$和${\delta }_r^2$。计算时，可直接用${\mu }_B$、${\delta }_B^2$代替。
  因此，在训练阶段，通过下面公式标准化输入：

（2）测试阶段
  在测试阶段，${\mu }_B$、${\delta }_B^2$计算原理和训练阶段相同。需要注意的是，这里的$x_i$是测试集的数据，m是测试集一次输入的batch数。
  因此，在测试阶段，通过下面公式标准化输入：

注意：测试阶段也进行标准化，并不是为了去优化训练，只是为了和训练解阶段保持一致，这样得到的测试结果才有意义。

五、Scale and Shift

  上述的标准化运算并没有引入额外的待优化变量，${\mu }_B$、${\delta }_B^2$ 均由统计得到，不需要参与梯度更新。实际上，为了提高 BN 层的表达能力，BN 层作者引入了“scale and shift”技巧，将$\hat{x}$变量再次映射变换：

  其中$\gamma$参数实现对标准化后的$\hat{x}$再次进行缩放，$\beta$参数实现对标准化的$\hat{x}$进行平移。不同的是，$\gamma$、$\beta$参数均由反向传播算法自动优化，实现网络层“按需”缩放平移数据的分布的目的。
于是，在测试阶段，标准化公式与缩放平移结合变为：

六、BN层实现

  在 TensorFlow 中，通过 layers.BatchNormalization()类可以非常方便地实现 BN 层：

# 插入BN层
layers.BatchNormalization()