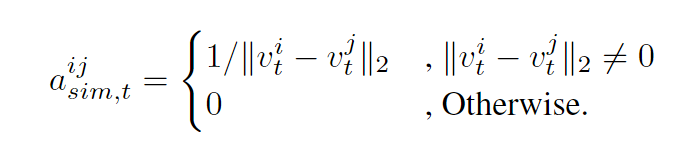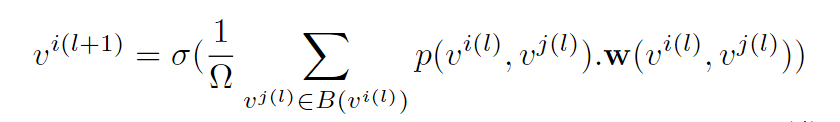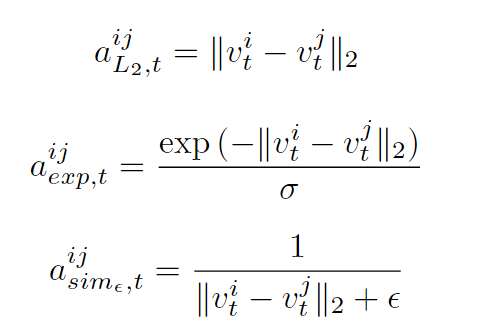论文: 论文地址
代码: 代码地址
作者在这篇文章中直接用GNN对目标的轨迹时空特征进行建模, 并用时序CNN进行预测, 代替了训练难度较大和速度较慢的RNN类方法.
0. Abstract
行人轨迹预测是一个比较有挑战性的任务, 有着许多的应用. 一个行人的轨迹不仅是由自己决定的, 而且受其周围目标的影响. 过去的方法都是学习每个行人自己的运动状态, 然而本文的方法是用一个GNN对整个场景的行人之间的interaction进行建模. 本文提出的方法叫Social-STGCNN, 是在STGCNN(一个基于骨架的action recognization的方法) 的基础上拓展到轨迹预测任务中的.
1. Introduction
过去的一些方法(例如Social-LSTM)是对每一个行人, 都分配一个循环结构的神经网络(lstm)来预测轨迹. 此外也有一些方法利用GAN来去生成未来的轨迹. 但是作者认为, 这些方法的训练成本都是相当高的, 能不能用一个统一的网络, 对行人之间的interaction进行建模.
作者还另起一段在道理上分析了为什么过去的网络是次优的. 主要是如下两个方面:
- 对每个行人用单独的网络进行预测, 并用池化来衡量行人之间的interaction. 这种方式是缺乏可解释性的. 相比之下, 本文用graph这种天然能够衡量节点之间关系的结构就具有了直观的可解释性.
- 池化会对信息造成损失.
因此, 作者提出了Social-STGCNN以解决上面的两个问题. 作者用一个具有时空(spatial-temporal)信息的GNN来衡量interaction, 并且显式地建模目标之间的影响力, 以此组成邻接矩阵, 然后用图卷积进行进一步的特征提取. 最后, 作者采用时序CNN来预测轨迹.
2. Related Work
这部分主要包含三个方面: 轨迹预测过去的工作, 图卷积的工作和时序CNN的工作.
3. Method
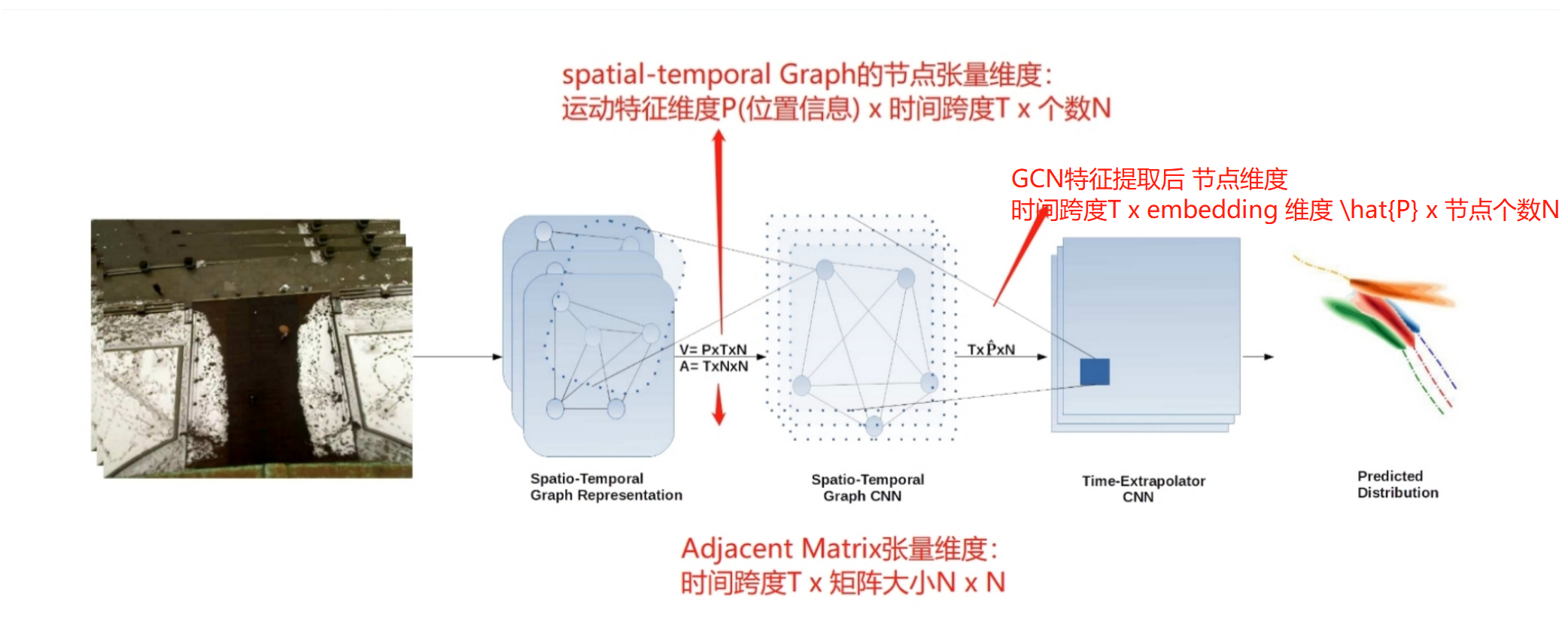
整个的Social-STGCNN由两部分组成, 一个是提取时空特征的STGCNN部分, 一个是预测轨迹的时序CNN(TXP-CNN)部分.
3.1. 空域建图
对于第 t t t帧, 我们考虑为第 t t t帧建图 G t = ( V t , E t ) G_t=(V_t,E_t) Gt=(Vt,Et). 我们以每个点在画面中的坐标表示为节点特征:
V t = { v t i } ∣ i = 1 N , v t i = ( x t i , y t i ) V_t = \{v_t^i\}|_{i=1}^N, ~~v_t^i=(x_t^i, y_t^i) Vt={vti}∣i=1N, vti=(xti,yti)
边 e t i j e_t^{ij} etij仅仅表示节点 i i i和 j j j之间是否相连. 然而, 对于邻接矩阵 A t = [ a s i m , t i j ] A_t=[a_{sim, t}^{ij}] At=[asim,tij]的构造, 是通过节点之间的欧氏距离定义的:
在建图之后, 我们就可以通过图卷积层来得到更新的node features了. 图卷积的公式如下:
其中
B
(
⋅
)
B(\cdot)
B(⋅)表示邻居节点的集合,
p
(
⋅
)
p(\cdot)
p(⋅)表示聚合函数,
w
(
⋅
)
\mathbf{w}(\cdot)
w(⋅)表示卷积核.
注意 B ( ⋅ ) B(\cdot) B(⋅)是通过最短路定义的:
B ( v i ) = { v j ∣ d ( v i , v j ≤ D ) } B(v^i) = \{v^j|d(v^i, v^j\le D)\} B(vi)={vj∣d(vi,vj≤D)}
其中 d d d表示最短路.
3.2. 时域建图
我们对每一帧进行上面的建图, 对于 T T T帧, 就可以得到一个时空图 G = ( V , E ) G=(V,E) G=(V,E). 其中 V = { v i } V=\{v^i\} V={vi}, v i = { v t i } ∣ t v^i=\{v_t^i\}|_t vi={vti}∣t. 边同理. 邻接矩阵也同理.
3.3. 轨迹预测
在得到时空的节点嵌入特征后, 时序CNN从时间维度对该嵌入进行特征提取即可预测未来的轨迹.
整个框图如下:
3.4. 具体实现
在实现时, 需要将图利用图的Lapalace矩阵进行归一化, 然后在进行卷积. 这是常规做法, 如下式:
A t = Λ t − 1 / 2 ( A t + I ) Λ t 1 / 2 , Λ t = d i a g ( A t ) A_t = \Lambda_t^{-1/2}(A_t+I)\Lambda_t^{1/2}, \Lambda_t = diag(A_t) At=Λt−1/2(At+I)Λt1/2,Λt=diag(At)
4. 实验
在消融实验部分, 作者比较了以下三种构造邻接矩阵的方式, 发现还是朴素的欧氏距离最好:
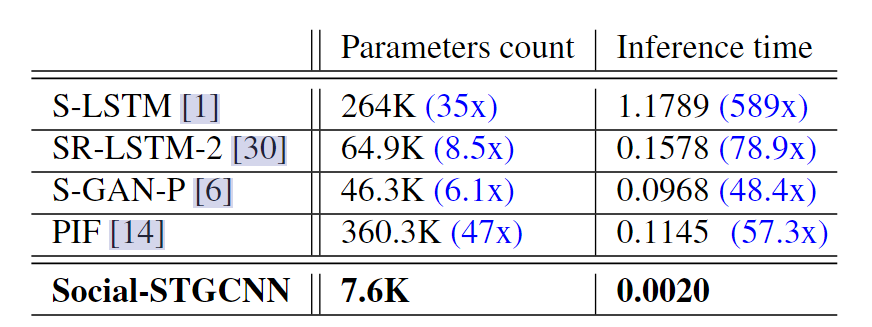
通过以下实验对比, 发现速度确实快很多: