码距：就单个编码 A: 00 而言，其码距为 1，因为其只需要改变一位就变成另一个编码。**在两个编码中，从 A 码到 B 码转换所需要改变的位数成为码距，**如 A: 00 要转换为 B: 11，码距为2。一般来说，码距越大，越利于纠错和检错。

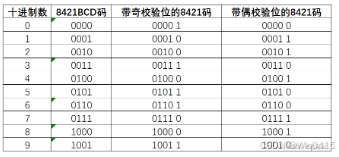
所谓码距，是指一个编码系统中任意两个合法编码之间至少有多少个二进制不同。例如，1000，1001码距为1 1000， 1011码距为2，码距的计算是对两个编码进行异或运算，并计算出语或运算结果中1的个数。4位8421码的码距为1，在传输过程中，该代码的一位或者多位发生错误，都将变成另外一个合法编，因此这种代码无差错检验能力。8421码是一种BCD码，其中每一位的“1”都代表一个固定的十进制数值。 从左到右看，每一位“1”分别代表数字“8”、“4”、“2”、“1”，因此得名8421码。 这种编码方式中，每位的权都是固定不变的，因此8421码是恒权码。

奇偶校验码 Parity Codes

奇偶校验码最简单,但只能检测出奇数位出错. 如果发生偶数位错误就无法检测. 但经研究是奇数位发生错误的概率大很多. 而且奇偶校验码无法检测出哪位出错.所以属于无法矫正错误的校验码。奇偶校验码是奇校验码和偶校验码的统称. 它们都是通过在要校验的编码上加一位校验位组成. 如果是奇校验加上校验位后,编码中1的个数为奇数个。如果是偶校验加上校验位后,编码中1的个数为偶数个。

从中可以看出，带奇偶校验位的8421码由4位信息为和一位校验位组成，码距为2，能检查出代码信息中的奇数位出错的情况，而错在哪些位置检查不出来的。也就是说，它只能发现错误，而不能校正错误。 

 常用的奇偶效验码有3种：水平奇偶校验码，垂直奇偶校验码和水平垂直校验码。 

1.水平奇偶校验码
        水平奇偶校验码。对每一个数据的编码添加校验位，使信息位与校验位处于同一行。

2.垂直奇偶校验码
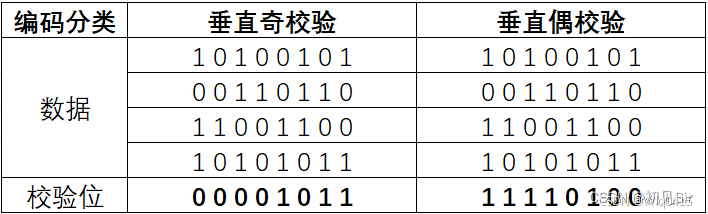
        垂直奇偶校验码。这种校验码把数据分成若干组，一组数据占一行，排列整齐，再加一行校验码，针对每一列采用奇校验或偶校验。

         对于32位数据10100101 00110110 11001100 10101011，其中垂直奇校验和垂直偶校验如下所示。

3.水平垂直校验码
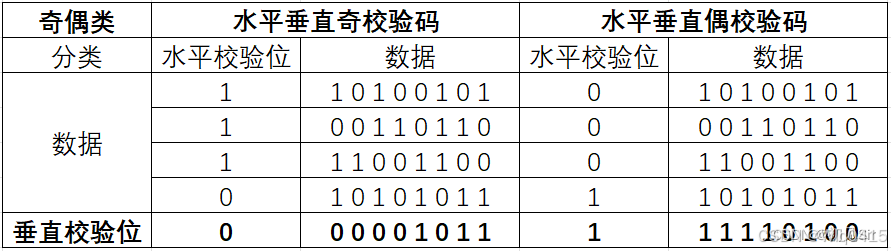
        水平垂直校验码。在垂直校验码的基础上，对每个数据再增加一位水平校验码，便构成水平垂直校验码。
        对于32位数据10100101 00110110 11001100 10101011，其水平垂直奇校验和偶校验如下所示：

循环冗余校验码  Cyclic Redundancy Check, CRC

CRC只能检错，不能纠错。CRC码利用生成多项式为k个数据位产生r个校验位进行编码,其编码长度为n=k+r所以又称 (n,k)码. CRC码广泛应用于数据通信领域和磁介质存储系统中.。

使用 CRC 编码，需要先约定一个生成多项式G(x)。生成多项式的最高位和最低位必须是1。假设原始信息由 m 位，则对应多项式 M(x)。生成校验码思想就是在原始信息位后追加若干个校验位，使得追加的信息能被G(x)整除。接收方接收到带校验位的信息，然后用 G(x)整除。余数为0，则没有错误，反之则发生错误。

例：假设原始信息串为 10110，CRC 的生成多项式为 G(x) = x4 + x + 1，求 CRC 校验码。

（1）**在原始信息位后面添0，假设生成多项式的阶为 r，则在原始信息位后添加 r 个 0，**本题中，G(x) 阶为 4，则在原始信息串后添加 4 个 0，得到的新串为 101100000，作为被除数。

（2）**由多项式得到除数，多项中x 的幂指数存在的位置1，不存在的位置0。**本题中，x的幂指数为0,1,4的变量都存在，而幂指数为2,3的不存在，因此得到串10011。

G(x) = x4 + x + 1 可以写成：G(x) = 1 * x4 + 0 * x3 + 0 * x2 + 1 * x1 + 1 * x0

所以：幂指数0,1,4 存在，2,3 不存在

即将 G(x) = 1 * x4 + 0 * x3 + 0 * x2 + 1 * x1 + 1 * x0 多项式中的 1、0 按序组合起来即可：10011

幂指数是数学中幂运算的一个组成部分，指的是乘方的次数。如 23中，2是底数，3是指数，意味着 3 个 2 相乘的结果是 8。

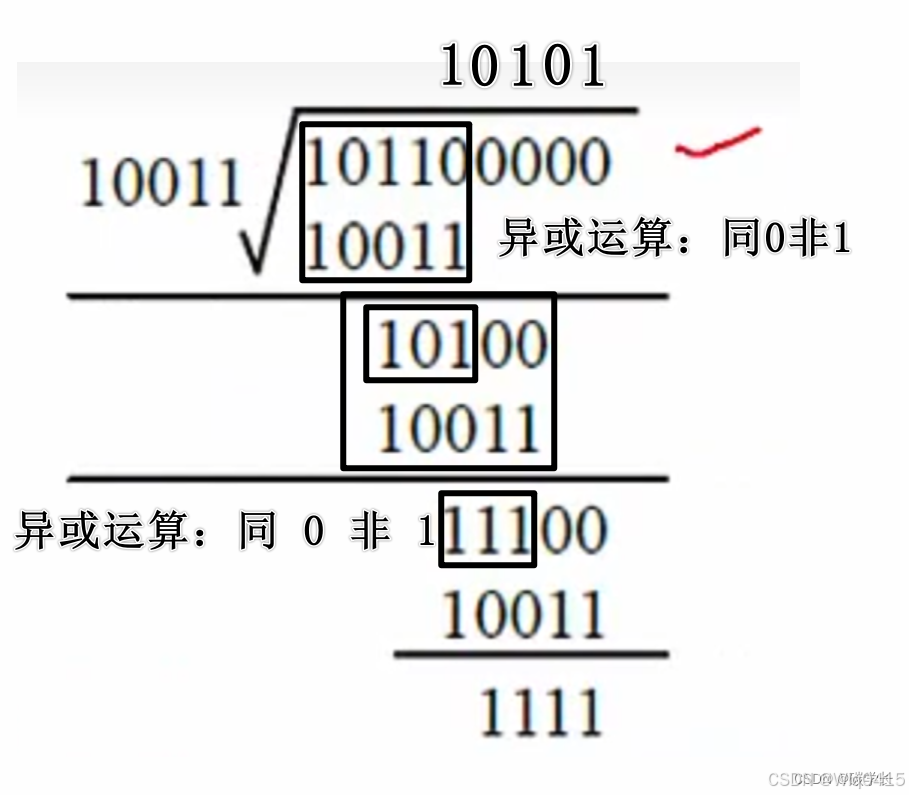
（3）生成CRC校验码，将前两步得出的被除数和除数进行模2除法运算（即不进位也不借位的除法运算）。除法过程如下图所示：模2运算，即异或运算，即 同 0 非 1，即两个数 位 相同 则为 0，不相同则为 1.

除数 10011

被除数 101100000

求余数：

得到余数 1111

注意：余数不足 r，则余数左边用若干个0补齐。如求得余数为11，r = 4，则补 2个0得到 0011。

（4）**生成最终发送信息串，将余数添加到原始信息后。**上例中，原始信息位 10110，添加余数 1111 后，结果为 10110 1111。发送方将此数据发送给接收方。

（5）**接收方进行校验。**接收方的 CRC 校验过程与生成过程类似，**接收方接收了带校验和的帧后，用多项式 G(x)来除（即用得到的结果 10110 1111 除以 10011）。**余数为0（因为第（4）部已经将余数加上去了，所以为0），则表示信息无错；否则要求发送方进行重传。

注意：收发信息双方需使用相同的生成多项式。

总结：

1、根据多项式的最高阶数 n（如xn），则在原始信息后补上 n 个 0，如原始信息位 1100，n为3，则被除数为 1100 000

2、根据多项式 G(x) = x3 + x + 1得到除数 如 1011

3、相除并进行模2运算 1100 0000 % 1011 = 10，得到的余数必须是 n 位，不够的在左侧补0，直至是 n 位，这里 余数是 10，只有两位，补0后，余数为 010.

4、原始信息位 1100 和 余数 010 组合：1100010 即为其 CRC 编码。

海明码  Hamming Code

海明码也是利用奇偶性来校验数据的. 它是一种多重奇偶校验检错系统,它通过在数据位之间插入k个校验位,来扩大码距,从而实现检错和纠错.

设原来数据有n位,要加入k位校验码.怎么确定k的大小呢? k个校验位可以有pow(2,k) (代表2的k次方) 个编码,其中有一个代表是否出错. 剩下pow(2,k)-1个编码则用来表示到底是哪一位出错. 因为n个数据位和k个校验位都可能出错，所以k满足pow(2,k)-1 >= n+k。

例：求信息 1011 的海明码。

1、校验位的位数和具体的数据位的位数之间的关系
**所有位都是编号，从最低位编号，从1开始递增，校验位处于2的n（n = 0,1,2…）次方中，即处于1,2,4,8,16,32，…位上，**其余位才能填充真正的数据位，若信息数据位1011，则可知，第1,2,4位为校验位，3,5,6,7位为数据位，用来从低位开始存放1011，得出信息为何校验位分布如下：

1011 为 4 位，校验位处于 1,2,4,8,16,32，…

则只需要 4 + 3（3个校验位），即第1位、第2位、第4位，不需要到第8位，因为 4 + 3 满足 小于 8了，即总共7位就够了。

同理 10位数，需要4位校验位，即第1位，第2位，第4位，第8位，不需要到第16位，因为 10 + 4 已经小于16了，即总共14位就够了。

2、计算校验码
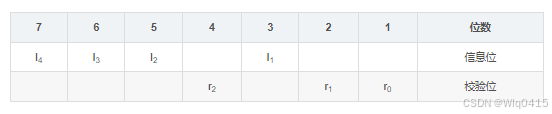
将**所有信息位的编号都拆分成二进制表示，**如下图所示：

上图中，7=4+2+1，表示7由第4位校验位（r2）和第2位校验位（r1）和第1位校验位（r0）共同校验，同理，第6位数据位6=4+2，第5位数据位5=4+1，第3位数据位3=2+1，前面知道，这些2的n次方都是校验位，可知，第4位校验位校验第7 6 5 三位数据位，因此，第4位校验位r2等于这三位数据位的值异或，第2位和第1位校验位计算原理同上。

计算出三个校验位后，可知最终要发送的海明校验码为1010101

原数据为1011，因为

第7位 为数据位 I4：

7 = 22 + 21 + 20

第6位 为数据位 I3：

6 = 22 + 21

第5位 为数据位 I2：

5 = 22 + 20

第3位 为数据位 I1：

3 = 21 + 20

第4位 为校验位r2

因此只要 第7、6、5、3 数据位的位数包含 4 的 ，则 r2 就校验这些位。

可以看到 7、6、5 都包含 22 即 4，所以 r2 校验位用来校验第7、6、5 的数据位，即 r2 用来校验 I4、I3、I2；

同理，第2位校验位为 r1，则包含 2 的 有：7、6、3，因为 7、6、3 都有 21，即 r1用来校验 I4、 I3、 I1

同理，第1位校验位为 r0，则包含 0的有：7、5、3，因为7、5、3都有20，即 r0 用来校验 I4、 I2、 I1

已知数据位I4、 I3、 I2、 I1（1011），已知校验位校验的数据位，则只需要根据对应的数据位进行 异或运算即可，即：

异或的运算法则为：0⊕0=0，1⊕0=1，0⊕1=1，1⊕1=0（同为0，异为1）

r2 = I4⊕I3⊕I2 = 1⊕0⊕1 = 0

r1 = I4⊕I3⊕I1 = 1⊕0⊕1 = 0

r0 = I4⊕I2⊕I1 = 1⊕1⊕1 = 1

所以海明校验码为：I4I3 I2r2I1r1r0 = 1010101

3、检错和纠错原理
接收方收到海明码之后，会将每一位校验位与其校验的位数分别异或，即做如下三组运算：

如果是偶校验，那么运算得到的结果应该全为0，如果是奇校验，应该全为1，才是正确。假设是偶校验，且接收到的数据为1011101（第四位出错），此时，运算的结果为：

这里不全位0，表明传输过程有误，并且按照r2r1r0排列为二进制100，这里指出的就是错误的位数，表示第100，即第4位出错，找到了出错位，纠错方法就是将该位逆转。

考点在于：设数据位是n位，校验位是k位，则 n 和 k 必须满足以下关系：2k-1 >= n + k。

32 + 6 (1,2,4,8,16,32) = 38，到不了第7位校验位（64），因为38 < 64.

所以32为至少主要6个校验位

D5 第10位，10 = 23 + 21 = 8 + 2，所以 D5 由P4P2校验。