1 概念
BP(Back Propagation)网络是一种按误差逆传播算法训练的多层前馈网络,是应用最广泛的神经网络模型之一。BP能学习和存贮大量的输入-输出模式映射关系,而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法,通过反向传播来不断调整网络的权值和阈值,使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层(input)、隐层(hide layer)和输出层(output layer)。出自百度百科
特点是根据误差的反向反馈改善信号传播。类似于最小二乘法的一种思想。
2 算法
2.1 算法流程
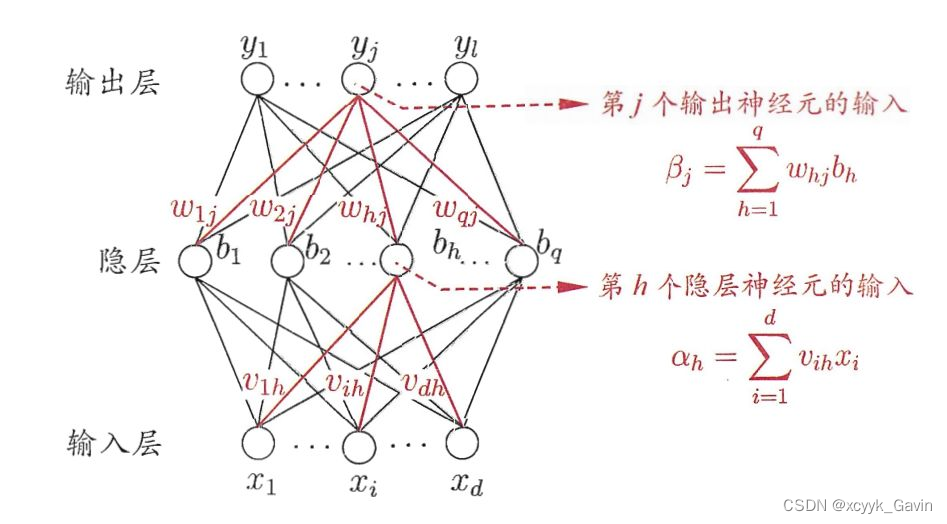
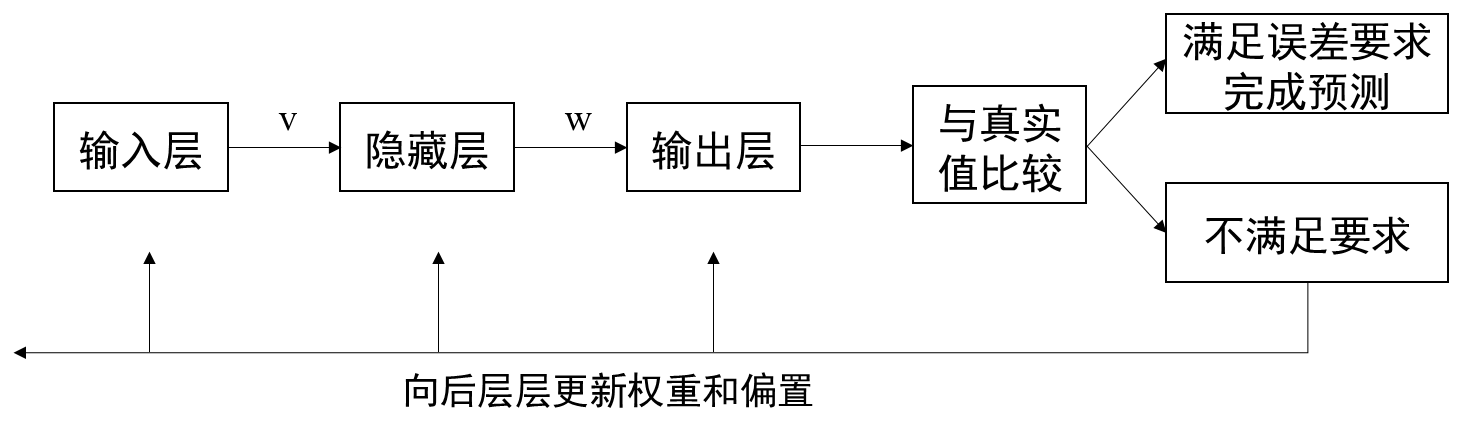
BP网络由输入层、隐藏层、输出层组成。
输入层用于信息输入,读入数据。
隐藏层用于处理数据,可以设置层数。
输出层用于信息输出,即目标结果。
v,w分别是输入层到隐藏层,隐藏层到输出层的权重。
第一阶段进行信号正向传播,即输入层—>隐含层—>输出层;第二阶段进行误差反向传播,即输出层—>隐含层—>输入层。依次调节隐含层到输出层的权重和偏置,输入层到隐含层的权重和偏置。
2.2 神经元
神经网络其实就是几层神经元,每层神经元里有几个神经元点。
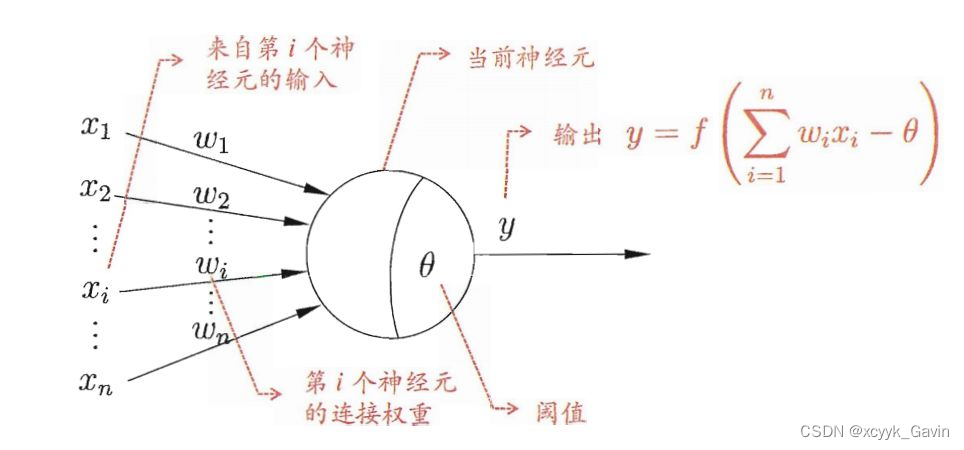
每一层神经元内部都不互相连接。每个神经元都接受来自上一层所有神经元的输入信号,每个信号都通过一个带有权重的连接(神经线)传递,神经元把这些信号按照权重加起来得到一个总输入值,然后将总输入值与神经元的阈值进行对比(模拟阈值电位),然后通过一个“激活函数”处理得到最终的输出(模拟细胞的激活),这个输出又会作为之后神经元的输入一层一层传递下去。
为方便写代码,可以设置每层神经元或者神经细胞数目一致。
2.3 激活函数
激活函数旨在在模型中引入非线性。若无激活函数(即激活函数是f(x)=x),那么无论神经网络有多少层,最终都是一个线性映射,则网络的逼近能力有限,线性映射无法解决线性不可分问题。因此引入非线性函数作为激励函数。
BP网络常用的激活函数有:
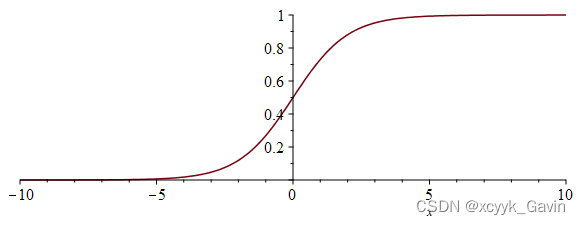
- Sigmoid(logistic).也叫S型生长曲线。可以把输入从负无穷大到正无穷大的信号变换成0~1之间输出。
f ( x ) = 1 1 + e − x f(x)=\dfrac{1}{1+e^{-x}} f(x)=1+e−x1
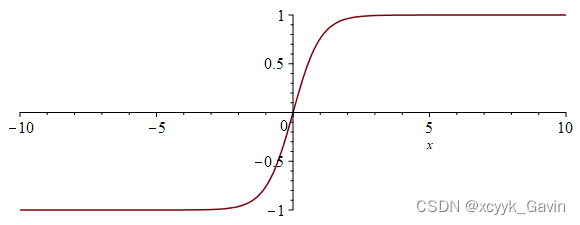
此函数具有很好的性质: f ′ ( x ) = f ( x ) ( 1 − f ( x ) ) f'(x)=f(x)(1-f(x)) f′(x)=f(x)(1−f(x)) - Tanh.解决Sigmoid函数中心不为0的缺点,但依旧有梯度易消失的缺点。
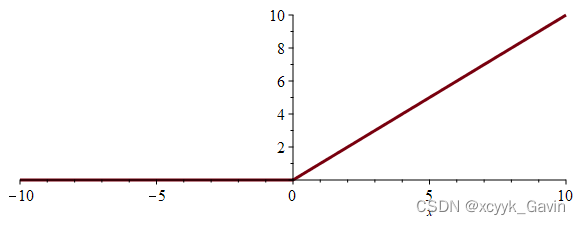
f ( x ) = e x − e − x e x + e − x f(x)=\dfrac{e^x-e^{-x}}{e^x+e^{-x}} f(x)=ex+e−xex−e−x - relu.通用激活函数,针对Sigmoid函数和tanh函数的缺点进行改进的,目前在大多数情况下使用。
f ( x ) = m a x ( 0 , x ) f(x)=max(0,x) f(x)=max(0,x)
3 工作过程
分为正向传播过程和反向传播过程。具体工作流程为:
3.1 正向传播过程
信息从输入层进入到网络,依次经过每层运算,得到最终输出层结果的过程。
计算过程主要涉及到矩阵乘法,用每一层的数值乘以对应的权重+偏置变量(激活函数)。
从输入层到隐藏层:
α
h
=
∑
i
=
1
d
v
i
h
x
i
\alpha_h=\sum\limits_{i=1}^dv_{ih}x_i
αh=i=1∑dvihxi经过隐藏层的激活函数为:
b
h
=
f
(
α
h
−
γ
h
)
b_h=f(\alpha_h-\gamma_h)
bh=f(αh−γh)其中,
v
i
h
v_{ih}
vih是输入层的第
i
i
i 个神经元和隐藏层第
h
h
h 个神经元之间的权重,
γ
h
\gamma_h
γh 是隐藏层第
h
h
h 个神经元的阈值。
从隐藏层到输出层: β j = ∑ h = 1 q w h j b h + θ j \beta_j=\sum\limits_{h=1}^qw_{hj}b_h+\theta_j βj=h=1∑qwhjbh+θj经过输出层的激活函数为: y k = f ( β j − θ j ) y_k=f(\beta_j-\theta_j) yk=f(βj−θj)其中, w h j w_{hj} whj是隐藏层的第 h h h 个神经元和输出层第 j j j 个神经元之间的权重, θ j \theta_j θj 是输出层第 j j j 个神经元的阈值。
因为参数是随机的,第一次计算结果跟真实误差很大,需根据误差去调整参数,直到误差最小,这时需要模型的反向传播。
3.2 反向传播过程
基本思想:通过计算输出层与期望值之间的误差来调整网络参数,目标使误差减小。
误差其实就是真实值与神经网络训练结果的差的平方和(也可选其它计算方式)。如下最小二乘法计算误差: E = 1 2 ∑ k = 1 l ( y k − y k ′ ) 2 E=\dfrac{1}{2}\sum\limits_{k=1}^l(y_k-y_k')^2 E=21k=1∑l(yk−yk′)2其中 y k y_k yk为训练的值, y k ′ y_k' yk′为实际值。
通过调整 d q + q + q l + l dq+q+ql+l dq+q+ql+l 个权重的大小(基于矩阵的链式求导法则),使损失函数不断变小的方法有:
- 梯度下降法:几何意义讲,函数总沿梯度方向变化最快。
- sgd:在梯度下降法基础上,sgd对单个训练样本进行参数更新,加快收敛速率。
- adam:在梯度下降法基础上,通过计算梯度的一阶矩估计和二阶矩估计而为不同的参数设计独立的自适应性学习率,加快收敛速率。
- lbfgs:sgd,Adam等都是在一阶法(梯度下降法)的基础上进行改进,加快收敛速率。而lbfgs在二阶泰勒展开式进行局部近似平均损失的基础上进行改进,以降低了迭代过程中的存储量,加快收敛速率。
其中最常用的是梯度下降法:对每一个需调整的参数求偏导,若偏导>0,则按偏导相反方向变化;若偏导<0,则按此方向变化。此处设定一个学习速率 η \eta η,学习速率不能太快或太慢。太快可能会导致越过最优解或结果在最优值附近徘徊而不收敛;太慢可能会收敛缓慢降低算法效率(具体需根据感觉调节,一般选值为0.01−0.8)。调节原则是反向层层调节。
首先隐层到输出层的权值调整值为: △ w h j = − ∣ η ∣ ∂ E ∂ w h j , w h j = △ w h j + w h j \triangle w_{hj}=-|\eta| \dfrac{\partial E}{\partial w_{hj}},w_{hj}=\triangle w_{hj}+w_{hj} △whj=−∣η∣∂whj∂E,whj=△whj+whj △ θ j = − ∣ η ∣ ∂ E ∂ θ j , θ j = △ θ j + θ j \triangle \theta_{j}=-|\eta| \dfrac{\partial E}{\partial \theta_{j}},\theta_{j}=\triangle \theta_{j}+\theta_{j} △θj=−∣η∣∂θj∂E,θj=△θj+θj输入层到隐层也类似。
通过不断使用所有数据记录进行训练,可得到一个分类模型。迭代的终止条件可以是:
- 设置最大迭代次数,比如使用数据集迭代100次后停止训练;
- 计算训练集在网络上的预测准确率,达到一定门限值后停止训练。
3.3 工作评价
超参数:学习率,隐含层层数,每个隐含层的神经元个数,激活函数,损失函数(代价函数)等。超参数很难确定,因为很难知道什么样的超参数会让模型表现更好。
(普通)参数:权重矩阵和偏置系数在确定了超参数之后可由模型算出,称之为普通参数或参数。
可通过以下量化指标来衡量BP神经网络的预测效果:
- MSE(均方误差):预测值与实际值之差平方的期望值。取值越小,模型准确度越高。
- RMSE(均方根误差):MSE的平方根,取值越小,模型准确度越高。
- MAE(平均绝对误差):绝对误差的平均值,能反映预测值误差的实际情况。取值越小,模型准确度越高。
- MAPE(平均绝对百分比误差):是MAE的变形,取值越小,模型准确度越高。
- R²: 将预测值跟只使用均值的情况下相比,结果越靠近 1 模型准确度越高。
4 MATLAB 实现BP神经网络
给出一个 算例代码:
clc,clear,close all % 清理命令区、清理工作区、关闭显示图形
format short % 数据类型
tic % 运算开始计时
% 构建网络
nntwarn off % 跳过浅层神经网络过时警告
P = [1,1,7,4,0,6,3,0,8,7;
1,3,6,7,9,6,1,0,0,4];
T = [1,8,2,8,0,3,7,8,2,4];
% 创建一个新的前向神经网络
net=newff(minmax(P),[10,1],{'tansig','purelin'},'traingdm');
% 当前输入层权值和阈值
inputWeights=net.IW{1,1} ;
inputbias=net.b{1} ;
% 当前网络层权值和阈值
layerWeights=net.LW{2,1} ;
layerbias=net.b{2} ;
% 设置训练参数
net.trainParam.show = 50;
net.trainParam.lr = 0.05;
net.trainParam.mc = 0.9;
net.trainParam.epochs = 10000;
net.trainParam.goal = 1e-3;
net.trainParam.showWindow = 0 ; % =0不显示网络训练对话框,=1 则显示。
% 调用 TRAINGDM 算法训练 BP 网络
[net,tr]=train(net,P,T);
% 对 BP 网络进行仿真
A = sim(net,P);
% 计算仿真误差
E = T - A; % 误差
MSE=mse(E) % 均方差
x=[1,3,6,7,9,6,1,0,0,4;
1,8,2,4,5,7,8,9,0,1];
sim(net,x)' % 预测结果
toc % 结束运算计时
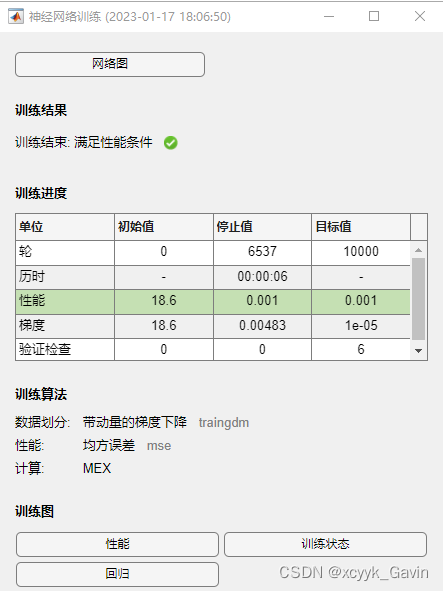
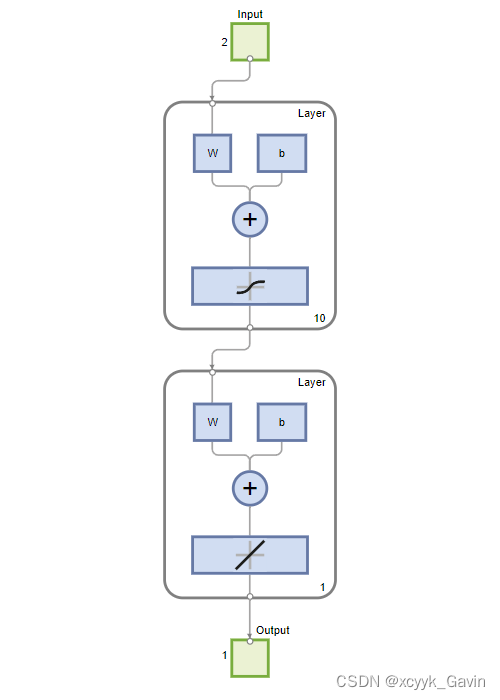
训练对话框及网络图:
文章参考:
https://zhuanlan.zhihu.com/p/485348369
https://blog.csdn.net/fanxin_i/article/details/80212906