手推一元线性回归【机器学习小白】
手推一元线性回归(附代码)
引言
由于经常做运维和编程工作,线性代数知识已经多年没有用了,基本已还给老师,线性回归的思路也是机器学习的基本思路,所以打算复习一下。顺便做个一元线性笔记,忘记的时候可以拿出来回顾一下。
本文主要以手推为主,程序作为辅助,程序语言选用python。
线性回归
提出问题
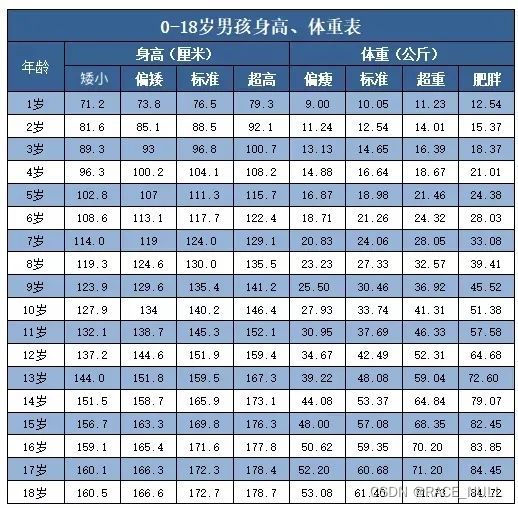
根据下表内容,预测指定年龄的儿童体重。例如:预测表中没有的,19岁儿童的标准体重。
用例说明
为方便手工推算计算,我取表中标准体重的前5个数据:[10.05,12.54,14.65,16.64,18.98],分别对应1岁到5岁年龄。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
#体重
weights=[10.05,12.54,14.65,16.64,18.98]
#年龄
ages=[1,2,3,4,5]
df=pd.DataFrame()
df['age']=ages
df['weight']=weights
# 散点图
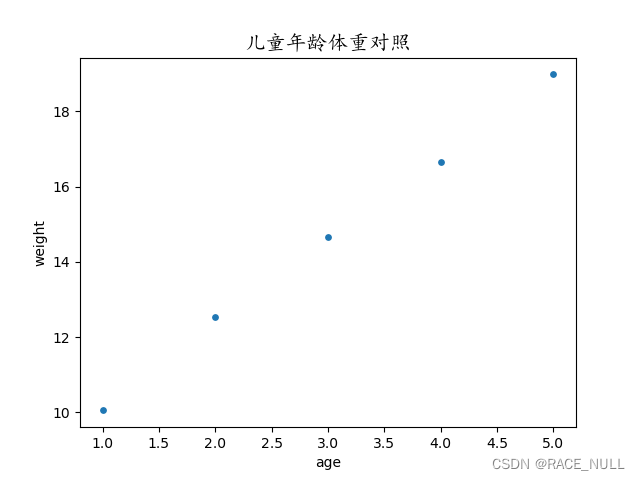
df.plot(kind='scatter', x='age', y='weight', c=None, s=15) # s:点的大小 c:点的颜色 c =np.squeeze(colors)
plt.title(u'儿童年龄体重对照', fontsize=15,fontdict=dict(family='KaiTi')) #楷体
plt.show()
分布图如下,看上去像是某种线性关系:
如果要预测儿童6岁时的体重,我们可以根据中学的知识,把这线散点拟合成直线方程:
y = ax + b
然后把6代入方程就可以预测出6岁时的体重。这就是线性回归。
一元线性回归就是找一条直线,并且让图中的散点尽可能靠近这条直线
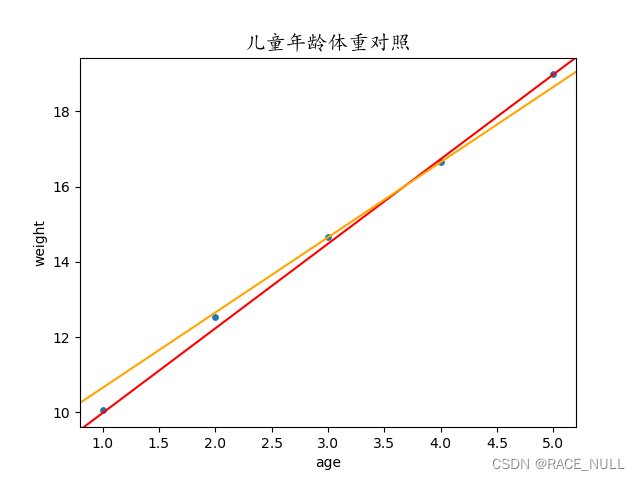
我们先随手画直线:
这又面临另一个问题:到底是红色直线更能拟合图中的散点?还是黄色直线?又或是其他直线呢?
解决这个问题就需要引入最小二乘法
假设我们的拟合直线为:
f
(
x
)
=
2.25
x
+
7.73
f(x)=2.25x+7.73
f(x)=2.25x+7.73
根据上面的例子,把5个样本(即1岁到5岁标准体重)分别代入上述方程可以得出5个预测结果:
y
1
^
=
f
(
x
1
)
=
2.25
×
1
+
7.73
=
9.98
\hat{y_1}=f(x_1)=2.25\times1+7.73=9.98
y1^=f(x1)=2.25×1+7.73=9.98
y
2
^
=
f
(
x
2
)
=
2.25
×
2
+
7.73
=
12.23
\hat{y_2}=f(x_2)=2.25\times2+7.73=12.23
y2^=f(x2)=2.25×2+7.73=12.23
y
3
^
=
f
(
x
3
)
=
2.25
×
3
+
7.73
=
14.48
\hat{y_3}=f(x_3)=2.25\times3+7.73=14.48
y3^=f(x3)=2.25×3+7.73=14.48
y
4
^
=
f
(
x
4
)
=
2.25
×
4
+
7.73
=
16.73
\hat{y_4}=f(x_4)=2.25\times4+7.73=16.73
y4^=f(x4)=2.25×4+7.73=16.73
y
5
^
=
f
(
x
5
)
=
2.25
×
5
+
7.73
=
18.98
\hat{y_5}=f(x_5)=2.25\times5+7.73=18.98
y5^=f(x5)=2.25×5+7.73=18.98
数学中的估计值一般用上面带尖的符号表示,如: θ ^ \hat{\theta} θ^, 读作theta hat。
##使用程序计算
上面为手算结果,很慢,且累。这才用了5个数据样本,现实中的数据远比这个多得多,所以需要程序辅助。
接上面的程序
y_head5_predict=([2.25*x+7.73 for x in df['age']]) #拟合结果
y_head5_predict的计算结果,即方程: f ( x ) = 2.25 x + 7.73 f(x)=2.25x+7.73 f(x)=2.25x+7.73 的预测结果
[9.98, 12.23, 14.48, 16.73, 18.98]
与真实结果做个对比
[ 9.98, 12.23, 14.48, 16.73, 18.98]
[10.05, 12.54, 14.65, 16.64, 18.98]
最小二乘法
损失函数
可以发现上面的预测结果与真实数据存在误差,毕竟预测结果是方程算出的嘛,和真实值当然会不一样了。那么如何来恒量这个误差呢?
残差公式
e = f ( x i ) − y i e=f(x_i)-y_i e=f(xi)−yi
把预测值与真实值相减便得出了这个误差。也可以写成这样:
y
i
^
−
y
i
=
ϵ
\hat{y_i}-y_i=\epsilon
yi^−yi=ϵ
但是这种算的结果有时是负数,计算起来不方便,于是就把它作平方处理。
损失函数原型
和方差(SSE)
S
S
E
=
∑
i
=
1
m
(
y
i
−
y
i
^
)
2
SSE=\sum_{i=1}^{m}(y_i-\hat{y_i})^2
SSE=∑i=1m(yi−yi^)2
均方误差(MSE)
M
S
E
=
S
S
E
N
=
1
N
∑
i
=
1
m
(
y
i
−
y
i
^
)
2
MSE=\frac{SSE}{N}=\frac{1}{N}\sum_{i=1}^{m}(y_i-\hat{y_i})^2
MSE=NSSE=N1∑i=1m(yi−yi^)2
均方根(RMSE)
R
M
S
E
=
M
S
E
=
1
N
∑
i
=
1
m
(
y
i
−
y
i
^
)
2
\Large RMSE=\sqrt{MSE}=\sqrt{\frac{1}{N}\sum_{i=1}^{m}(y_i-\hat{y_i})^2}
RMSE=MSE=N1∑i=1m(yi−yi^)2
总之,这些公式的值最越小,说明损失越小,线性方程就能更好地拟合样本数据。
参数估计——最小二乘法
以上面例子的方程:
f
(
x
)
=
a
x
+
b
f(x)=ax+b
f(x)=ax+b
找出最合适的参数a和b,就是展开后:
f
(
a
,
b
)
=
∑
i
=
1
m
(
y
i
−
y
i
^
)
2
=
∑
i
=
1
m
(
y
i
−
(
a
x
i
+
b
)
)
2
f(a,b)=\sum_{i=1}^{m}(y_i-\hat{y_i})^2=\sum_{i=1}^{m}(y_i-(ax_i+b))^2
f(a,b)=∑i=1m(yi−yi^)2=∑i=1m(yi−(axi+b))2
然后求出这个函数的最小值,这就是求线性回归的最小二乘法。
根据微积分知识,就是把函数
f
(
a
,
b
)
f(a,b)
f(a,b)分别对a和b求偏导,然后令偏导等于0。
对参数a的求导过程
令
u
=
y
i
−
(
a
x
i
+
b
)
u=y_i-(ax_i+b)
u=yi−(axi+b),根据链式法则(注意:x、y和b看成常数):
(
∑
i
=
1
m
(
y
i
−
(
a
x
i
+
b
)
)
2
)
′
\big(\sum_{i=1}^{m}(y_i-(ax_i+b))^2\big)\prime
(∑i=1m(yi−(axi+b))2)′
=
∑
i
=
1
m
2
(
y
i
−
(
a
x
i
+
b
)
)
(
y
i
−
(
a
x
i
+
b
)
)
′
=\sum_{i=1}^{m}2(y_i-(ax_i+b))(y_i-(ax_i+b))\prime
=∑i=1m2(yi−(axi+b))(yi−(axi+b))′
=
∑
i
=
1
m
2
(
y
i
−
(
a
x
i
+
b
)
)
(
y
i
′
−
(
a
x
i
)
′
−
b
′
)
=\sum_{i=1}^{m}2(y_i-(ax_i+b))(y_i\prime-(ax_i)\prime-b\prime)
=∑i=1m2(yi−(axi+b))(yi′−(axi)′−b′)
=
2
∑
i
=
1
m
(
y
i
−
(
a
x
i
+
b
)
)
(
0
−
x
i
−
0
)
=2\sum_{i=1}^{m}(y_i-(ax_i+b))(0-x_i-0)
=2∑i=1m(yi−(axi+b))(0−xi−0)
=
2
∑
i
=
1
m
(
a
x
i
+
b
−
y
i
)
x
i
=2\sum_{i=1}^{m}(ax_i+b-y_i)x_i
=2∑i=1m(axi+b−yi)xi
对参数b的求导过程
令
u
=
y
i
−
(
a
x
i
+
b
)
u=y_i-(ax_i+b)
u=yi−(axi+b),根据链式法则(注意:x、y和a看成常数):
(
∑
i
=
1
m
(
y
i
−
(
a
x
i
+
b
)
)
2
)
′
\big(\sum_{i=1}^{m}(y_i-(ax_i+b))^2\big)\prime
(∑i=1m(yi−(axi+b))2)′
=
∑
i
=
1
m
2
(
y
i
−
(
a
x
i
+
b
)
)
(
y
i
−
(
a
x
i
+
b
)
)
′
=\sum_{i=1}^{m}2(y_i-(ax_i+b))(y_i-(ax_i+b))\prime
=∑i=1m2(yi−(axi+b))(yi−(axi+b))′
=
∑
i
=
1
m
2
(
y
i
−
(
a
x
i
+
b
)
)
(
y
i
′
−
(
a
x
i
)
′
−
b
′
)
=\sum_{i=1}^{m}2(y_i-(ax_i+b))(y_i\prime-(ax_i)\prime-b\prime)
=∑i=1m2(yi−(axi+b))(yi′−(axi)′−b′)
=
2
∑
i
=
1
m
(
y
i
−
(
a
x
i
+
b
)
)
(
0
−
0
−
1
)
=2\sum_{i=1}^{m}(y_i-(ax_i+b))(0-0-1)
=2∑i=1m(yi−(axi+b))(0−0−1)
=
2
∑
i
=
1
m
(
a
x
i
+
b
−
y
i
)
=2\sum_{i=1}^{m}(ax_i+b-y_i)
=2∑i=1m(axi+b−yi)
估算参数
解如下方程组:
{
∂
∂
a
ϵ
=
2
∑
i
=
1
m
(
a
x
i
+
b
−
y
i
)
x
i
=
0
∂
∂
a
ϵ
=
2
∑
i
=
1
m
(
a
x
i
+
b
−
y
i
)
=
0
\begin{cases} \frac{\partial}{\partial{a}}\epsilon=2\sum_{i=1}^{m}(ax_i+b-y_i)x_i=0\\ \frac{\partial}{\partial{a}}\epsilon=2\sum_{i=1}^{m}(ax_i+b-y_i)=0 \end{cases}
{∂a∂ϵ=2∑i=1m(axi+b−yi)xi=0∂a∂ϵ=2∑i=1m(axi+b−yi)=0
(长时间没用过高数,只能用笨办法)
式子1展开、转化:
∑
i
=
1
m
(
a
x
i
+
b
−
y
i
)
x
i
=
0
\sum_{i=1}^{m}(ax_i+b-y_i)x_i=0
∑i=1m(axi+b−yi)xi=0
∑
i
=
1
m
(
a
x
i
2
+
b
x
i
−
y
i
x
i
)
=
0
\sum_{i=1}^{m}(ax_i^2+bx_i-y_ix_i)=0
∑i=1m(axi2+bxi−yixi)=0
∑
i
=
1
m
a
x
i
2
+
∑
i
=
1
m
b
x
i
−
∑
i
=
1
m
y
i
x
i
=
0
\sum_{i=1}^{m}ax_i^2+\sum_{i=1}^{m}bx_i-\sum_{i=1}^{m}y_ix_i=0
∑i=1maxi2+∑i=1mbxi−∑i=1myixi=0
a
∑
i
=
1
m
x
i
2
+
b
∑
i
=
1
m
x
i
−
∑
i
=
1
m
y
i
x
i
=
0
a\sum_{i=1}^{m}x_i^2+b\sum_{i=1}^{m}x_i-\sum_{i=1}^{m}y_ix_i=0
a∑i=1mxi2+b∑i=1mxi−∑i=1myixi=0
式子2展开、转化:
∑
i
=
1
m
(
a
x
i
+
b
−
y
i
)
=
0
\sum_{i=1}^{m}(ax_i+b-y_i)=0
∑i=1m(axi+b−yi)=0
∑
i
=
1
m
a
x
i
+
∑
i
=
1
m
b
−
∑
i
=
1
m
y
i
=
0
\sum_{i=1}^{m}ax_i+\sum_{i=1}^{m}b-\sum_{i=1}^{m}y_i=0
∑i=1maxi+∑i=1mb−∑i=1myi=0
a
∑
i
=
1
m
x
i
+
m
b
−
∑
i
=
1
m
y
i
=
0
a\sum_{i=1}^{m}x_i+mb-\sum_{i=1}^{m}y_i=0
a∑i=1mxi+mb−∑i=1myi=0
初中知识,用代入消元法:
转化式子2:
b
=
∑
i
=
1
m
y
i
m
−
a
∑
i
=
1
m
x
i
m
=
y
ˉ
−
a
x
ˉ
\Large b=\frac{\sum_{i=1}^{m}y_i}{m}-\frac{a\sum_{i=1}^{m}x_i}{m}=\bar{y}-a\bar{x}
b=m∑i=1myi−ma∑i=1mxi=yˉ−axˉ
代入式子1:
a
∑
i
=
1
m
x
i
2
+
(
y
ˉ
−
a
x
ˉ
)
∑
i
=
1
m
x
i
−
∑
i
=
1
m
y
i
x
i
=
0
a\sum_{i=1}^{m}x_i^2+(\bar{y}-a\bar{x})\sum_{i=1}^{m}x_i-\sum_{i=1}^{m}y_ix_i=0
a∑i=1mxi2+(yˉ−axˉ)∑i=1mxi−∑i=1myixi=0
a
∑
i
=
1
m
x
i
2
+
y
ˉ
∑
i
=
1
m
x
i
−
a
x
ˉ
∑
i
=
1
m
x
i
−
∑
i
=
1
m
y
i
x
i
=
0
a\sum_{i=1}^{m}x_i^2+\bar{y}\sum_{i=1}^{m}x_i-a\bar{x}\sum_{i=1}^{m}x_i-\sum_{i=1}^{m}y_ix_i=0
a∑i=1mxi2+yˉ∑i=1mxi−axˉ∑i=1mxi−∑i=1myixi=0
a
(
∑
i
=
1
m
x
i
2
−
x
ˉ
∑
i
=
1
m
x
i
)
+
y
ˉ
∑
i
=
1
m
x
i
−
∑
i
=
1
m
y
i
x
i
=
0
a(\sum_{i=1}^{m}x_i^2-\bar{x}\sum_{i=1}^{m}x_i)+\bar{y}\sum_{i=1}^{m}x_i-\sum_{i=1}^{m}y_ix_i=0
a(∑i=1mxi2−xˉ∑i=1mxi)+yˉ∑i=1mxi−∑i=1myixi=0
a
=
∑
i
=
1
m
y
i
x
i
−
y
ˉ
∑
i
=
1
m
x
i
∑
i
=
1
m
x
i
2
−
x
ˉ
∑
i
=
1
m
x
i
\Large a=\frac{\sum_{i=1}^{m}y_ix_i-\bar{y}\sum_{i=1}^{m}x_i}{\sum_{i=1}^{m}x_i^2-\bar{x}\sum_{i=1}^{m}x_i}
a=∑i=1mxi2−xˉ∑i=1mxi∑i=1myixi−yˉ∑i=1mxi
到这里,把样本数据代入函数已经可以算出参数a的值了。
上代码:
# 最小二乘法估出参数
x_bar = np.mean(ages)
y_bar = np.mean(weights)
a_param = np.dot(ages, weights) - y_bar * np.sum(ages)
a_param = a_param / (np.sum(np.square(ages)) - x_bar * np.sum(ages))
b_param = y_bar - a_param * x_bar
参数a的结果,即斜率:
2.1960000000000037
参数b的结果,即截距:
7.9839999999999876
估算过程补充说明
- 公式
a = ∑ i = 1 m y i x i − y ˉ ∑ i = 1 m x i ∑ i = 1 m x i 2 − x ˉ ∑ i = 1 m x i \Large a=\frac{\sum_{i=1}^{m}y_ix_i-\bar{y}\sum_{i=1}^{m}x_i}{\sum_{i=1}^{m}x_i^2-\bar{x}\sum_{i=1}^{m}x_i} a=∑i=1mxi2−xˉ∑i=1mxi∑i=1myixi−yˉ∑i=1mxi
这个公式若使用手算还可以再转化:
a = ∑ i = 1 m y i x i − 1 m ∑ i = 1 m y i ∑ i = 1 m x i ∑ i = 1 m x i 2 − x ˉ ∑ i = 1 m x i \Large a=\frac{\sum_{i=1}^{m}y_ix_i-\frac{1}{m}\sum_{i=1}^{m}y_i\sum_{i=1}^{m}x_i}{\sum_{i=1}^{m}x_i^2-\bar{x}\sum_{i=1}^{m}x_i} a=∑i=1mxi2−xˉ∑i=1mxi∑i=1myixi−m1∑i=1myi∑i=1mxi
a = ∑ i = 1 m y i x i − x ˉ ∑ i = 1 m y i ∑ i = 1 m x i 2 − x ˉ ∑ i = 1 m x i \Large a=\frac{\sum_{i=1}^{m}y_ix_i-\bar{x}\sum_{i=1}^{m}y_i}{\sum_{i=1}^{m}x_i^2-\bar{x}\sum_{i=1}^{m}x_i} a=∑i=1mxi2−xˉ∑i=1mxi∑i=1myixi−xˉ∑i=1myi
a = ∑ i = 1 m y i ( x i − x ˉ ) ∑ i = 1 m x i 2 − x ˉ ∑ i = 1 m x i \Large a=\frac{\sum_{i=1}^{m}y_i(x_i-\bar{x})}{\sum_{i=1}^{m}x_i^2-\bar{x}\sum_{i=1}^{m}x_i} a=∑i=1mxi2−xˉ∑i=1mxi∑i=1myi(xi−xˉ) - 代码说明
np.dot(ages, weights)
这行代码为向量的点乘(内积),公式如下:
若有向量:
a
=
[
a
1
,
a
2
,
a
3
,
…
,
a
n
]
a=[a_1,a_2,a_3,\ldots,a_n]
a=[a1,a2,a3,…,an]
b
=
[
b
1
,
b
2
,
b
3
,
…
,
b
n
]
b=[b_1,b_2,b_3,\ldots,b_n]
b=[b1,b2,b3,…,bn]
向量a和b的点积公式为:
a
⃗
∙
b
⃗
=
a
1
b
1
+
a
2
b
2
+
a
3
b
3
+
…
+
a
n
b
n
\Large \vec{a}\bullet\vec{b}=a_1b_1+a_2b_2+a_3b_3+\ldots+a_nb_n
a∙b=a1b1+a2b2+a3b3+…+anbn
所以
∑
i
=
1
m
y
i
x
i
\sum_{i=1}^{m}y_ix_i
∑i=1myixi可以用向量点乘方式来计算。
用程序验证手推结果
下面用sklearn的线性回归模型验证上面的推导结果:
# 验证上面手推最小二乘法的结果
# sklearn中,数据都应该是二维矩阵,这里需要转换
x_train = np.array(ages).reshape(-1, 1)
y_train = np.array(weights).reshape(-1, 1)
lr = LinearRegression()
lr.fit(x_train, y_train)
print("斜率:", lr.coef_)
print("截距:", lr.intercept_)
代码输出结果
斜率: [[2.196]]
截距: [7.984]
至此,一元线性回归模型的手工推导完成。要预测后面的结果只需代入函数:
f
(
x
i
)
=
2.196
x
i
+
7.984
\Large f(x_i)=2.196x_i+7.984
f(xi)=2.196xi+7.984
多元线性回归
上面的例子只是用年龄来对身高作出预测,输入就只有年龄这一项,在现实中还可以引入多个输入项对模型进行训练。例如可以加入身高、饮食量、运动时间等。
根据一元线性回归
f
(
x
)
=
a
x
+
b
f(x)=ax+b
f(x)=ax+b
假设每个样本有d个输入项,多元线性回归变为
f
(
x
i
)
=
ω
1
x
i
1
+
ω
2
x
i
2
+
…
+
ω
d
x
i
d
+
b
\Large f(x_i)=\omega_1x_{i1}+\omega_2x_{i2}+\ldots+\omega_dx_{id}+b
f(xi)=ω1xi1+ω2xi2+…+ωdxid+b
有的会加上一个随机误差项
ϵ
\epsilon
ϵ,公式不一样但思想相同。
y
=
β
0
+
β
1
x
1
+
β
2
x
2
+
…
+
β
k
x
k
+
ϵ
\Large y=\beta_0+\beta_1x_1+\beta_2x_2+\ldots+\beta_kx_k+\epsilon
y=β0+β1x1+β2x2+…+βkxk+ϵ
求解过程同样是用最小二乘法找出最适合的
ω
\omega
ω和b。而
ω
\omega
ω的集合就是机器学习中高大上的参数矩阵。
f
(
x
i
)
=
ω
T
x
i
+
b
\Large f(x_i)=\omega^Tx_i+b
f(xi)=ωTxi+b
在这里x与
ω
\omega
ω都变为矩阵。而求解过程也比一元线性回归要复杂得多,这里就不做手工推算了,直接使用sklearn集成好的库,用代码体验一下。
#增加一个身高输入项
ages_highs = [
[1, 2, 3, 4, 5], #年龄
[76.5,88.5,96.8,104.1,111.3] #标准身高
]
x_train =np.array(ages_highs).T #这里需要做矩阵转置
y_train = np.array(weights).reshape(-1, 1)
lr = LinearRegression()
lr.fit(x_train, y_train)
print("斜率:", lr.coef_)
print("截距:", lr.intercept_)
lr.predict([[6,117.7]])
输出结果
斜率: [[1.67268574 0.06142186]]
截距: [3.69184031]
array([[20.95730786]])
预测结果:6岁,标准身高为117.7的儿童,体重为20.957。