📃博客主页: 小镇敲码人
💚代码仓库,欢迎访问
🚀 欢迎关注:👍点赞 👂🏽留言 😍收藏
🌏 任尔江湖满血骨,我自踏雪寻梅香。 万千浮云遮碧月,独傲天下百坚强。 男儿应有龙腾志,盖世一意转洪荒。 莫使此生无痕度,终归人间一捧黄。🍎🍎🍎
❤️ 什么?你问我答案,少年你看,下一个十年又来了 💞 💞 💞
【哈希的常见应用】之位图和布隆过滤器
前言:上篇博客我们介绍了
unordered_map和unordered_set的封装,它们的底层都是哈希表,今天这篇博客让我们来一起学习一下哈希思想在解决海量数据上的其它应用。
位图
位图的引入
看下面这道面试题,思考解决办法:
常见的解决办法:
set容器+二分算法set+find
但是看数据量我们发现这两种办法都是不行的。
16G内存太大了,目前手机的最大内存是:
当然电脑你也可以自己配置更大的内存条,但是这种一般都是定制的,没有在市场广泛的流通,因为成本太高了:
所以如果我们使用set直接存储这40亿个无符号的整数,显然是不太现实的。
这个时候就需要使用到我们的位图数据结构:
像它的名字一样位图就是使用每一个
bit位来标记数据,一个bit位就代表一个数据。
这样我们一个4字节的变量就可以标记32个数据,将大大减少需要的内存空间,这样就可以在内存中标记这40亿个无符号整数了。
位图的实现
位图的结构设计
我们利用C++模板可以传整数的语法特性,在创建位图结构的时候,就给位图传上一个无符号整型值N,这个值表示位图结构标记值的最大值。我们使用vector来作为位图结构的底层数据结构,vector的大小是N/32+1,因为要考虑不能整除的情况,我们干脆都加一个1。
template<size_t N>
class bitset
{
private:
vector<int> _bitset;
public:
bitset()
{
_bitset.resize(N / 32 + 1);
}
}
位图的标记
假如我们此时要标记 50 50 50这个数,位图标记50,应该如何来实现呢?我们画图来表示更加的形象:
理解左移右移和小端大端模式
我们使用一段代码来带大家更深入的了解一下:
int main()
{
int a = 1;
a <<= 8;
return 0;
}
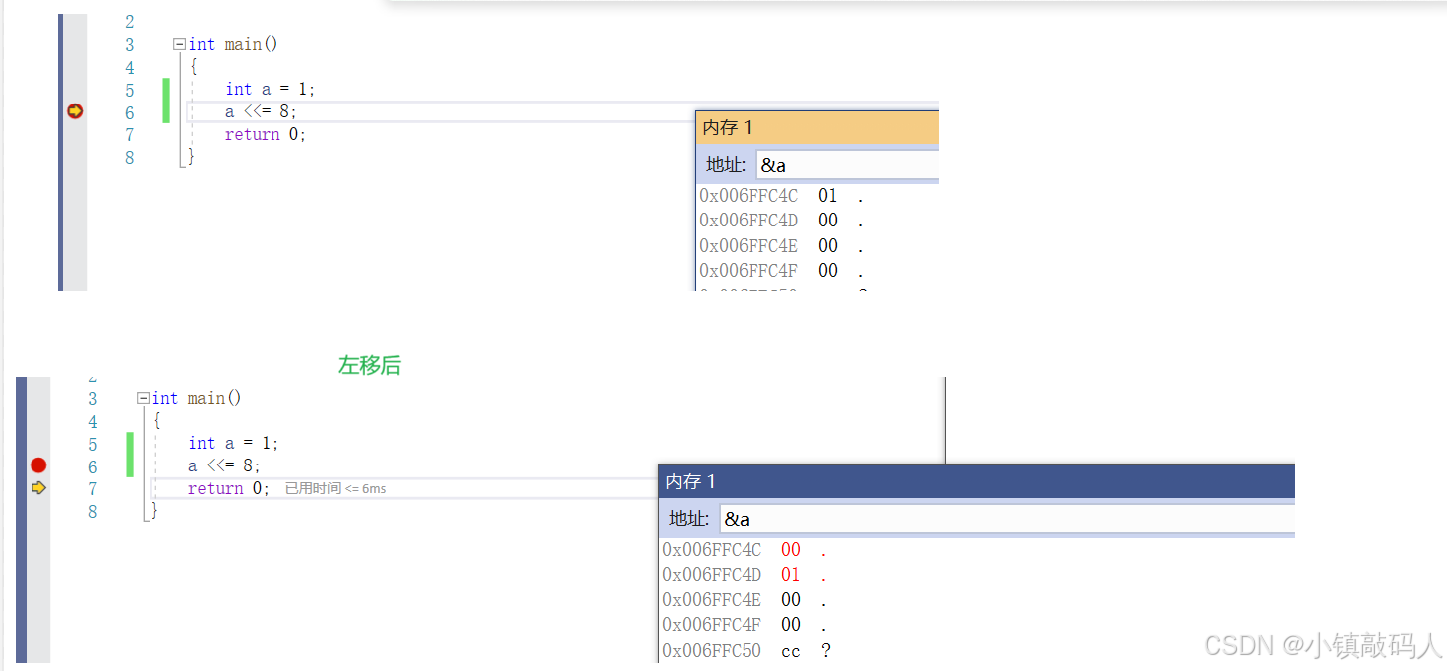
就是这段简单的代码,大家猜测一下a <<= 8前后它在内存中具体的存储情况是怎样呢?我们这台机器是小端模式
内存布局(调试):
代码实现:
Self& set(size_t pos)
{
size_t i = pos / 32;
size_t j = pos % 32;
_bitset[i] |= 1 << j;
return *this;
}
位图的去标记
Self& reset(size_t pos)
{
size_t i = pos / 32;
size_t j = pos % 32;
_bitset[i] &= ~(1 << j);
return *this;
}
除了i下标变量的j bit位与上为0,其它为都与上1(相当于不变)。
位图查找某个数是否在位图中
bool test(size_t pos)
{
size_t i = pos / 32;
size_t j = pos % 32;
return (_bitset[i] >> j) & 1;
}
基本的位操作,也可以(_bitset[i] & (1 << j))是一样的效果。
位图的完整代码
template<size_t N>
class bitset
{
private:
vector<int> _bitset;
public:
bitset()
{
_bitset.resize(N / 32 + 1);
}
typedef bitset<N> Self;
Self& set(size_t pos)
{
size_t i = pos / 32;
size_t j = pos % 32;
_bitset[i] |= 1 << j;
return *this;
}
Self& reset(size_t pos)
{
size_t i = pos / 32;
size_t j = pos % 32;
_bitset[i] &= ~(1 << j);
return *this;
}
bool test(size_t pos)
{
size_t i = pos / 32;
size_t j = pos % 32;
return (_bitset[i] >> j) & 1;
}
};
位图的测试
void test_bitset()
{
bitset<100> bs1;
bs1.set(50);
bs1.set(30);
bs1.set(90);
for (size_t i = 0; i < 100; i++)
{
if (bs1.test(i))
{
cout << i << "->" << "在" << endl;
}
else
{
cout << i << "->" << "不在" << endl;
}
}
bs1.reset(90);
bs1.set(91);
cout << endl << endl;
for (size_t i = 0; i < 100; i++)
{
if (bs1.test(i))
{
cout << i << "->" << "在" << endl;
}
else
{
cout << i << "->" << "不在" << endl;
}
}
bitset<-1> bs2;
bitset<UINT_MAX> bs3;
bitset<0xffffffff> bs4;
}
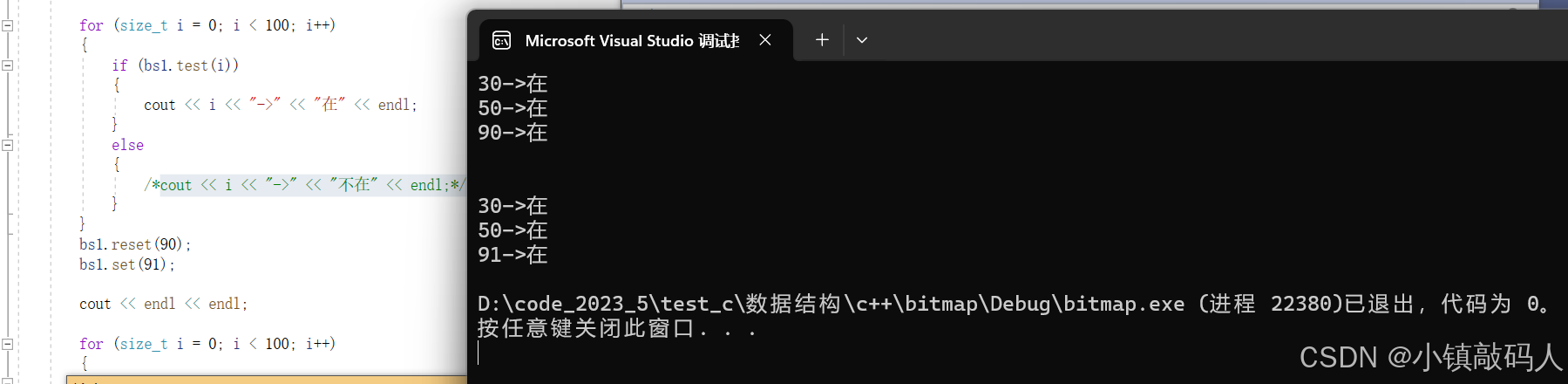
运行结果:
为了方便看,我们将不在的调试信息没有打印出来。
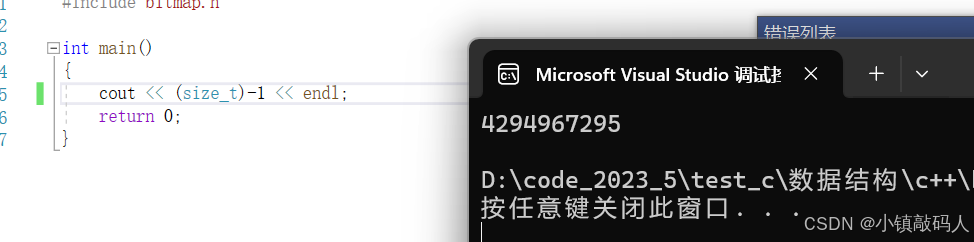
这里-1大概是40多亿,也就是bitset可以标记42多亿个数。只需要大约500M的内存空间。
位图的应用
位图只能存整数(不会误判),如果用哈希映射去存字符串,这就叫布隆过滤器了,这也是位图的缺陷,
布隆过滤器
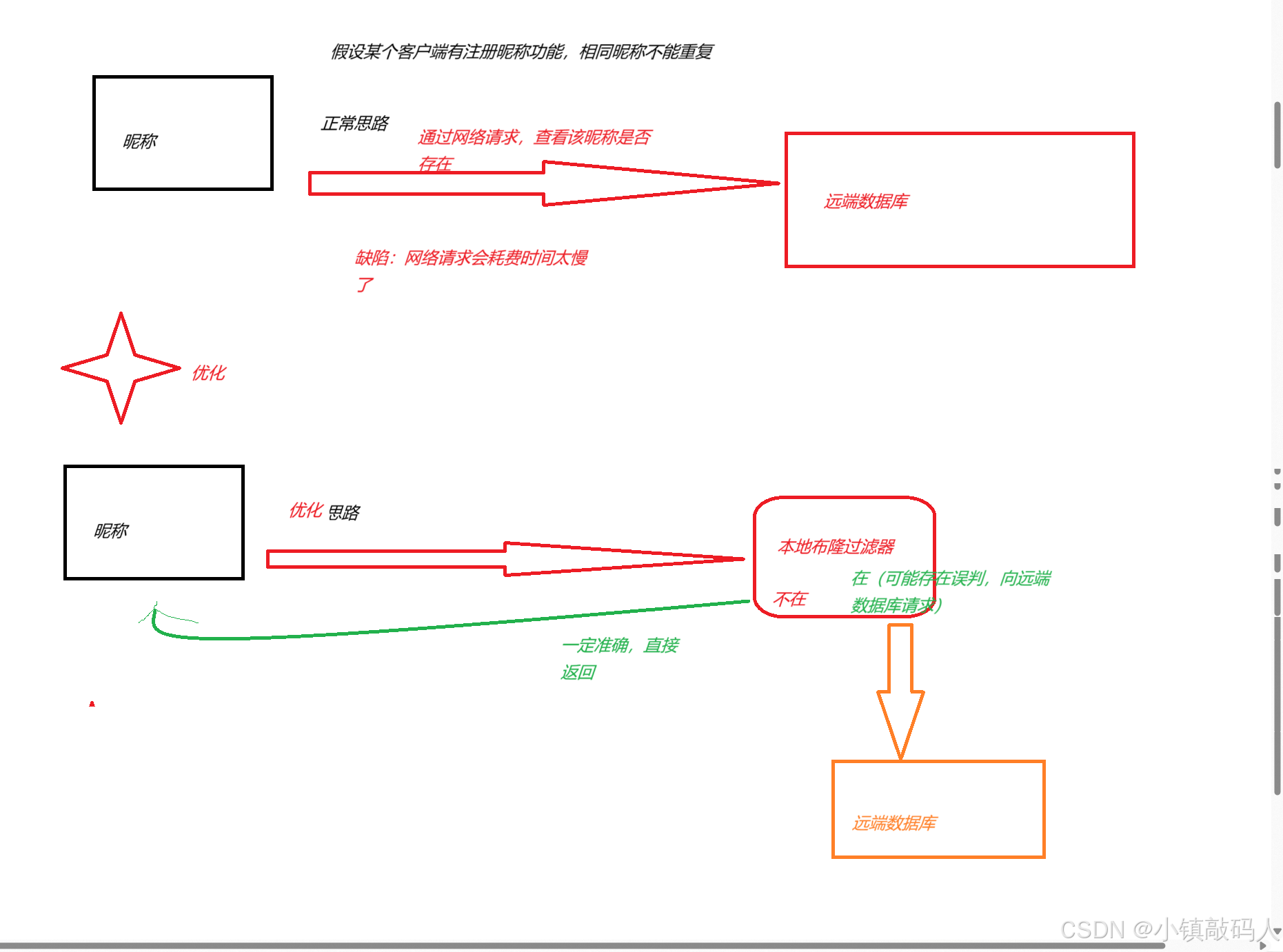
布隆过滤器的引入
位图可能会存在误判,我们需要使用布隆过滤器来减少误判的概率。
布隆过滤器的实现
布隆过滤器的模板参数及其类结构
struct SDBMHash
{
unsigned int operator()(const char* str)
{
//SDB
unsigned int hash = 0;
while (*str)
{
// equivalent to: hash = 65599*hash + (*str++);
hash = (*str++) + (hash << 6) + (hash << 16) - hash;
}
return (hash & 0x7FFFFFFF);
}
};
struct BKDRHash
{
// BKDR Hash Function
unsigned int operator()(const char* str)
{
unsigned int seed = 131; // 31 131 1313 13131 131313 etc..
unsigned int hash = 0;
while (*str)
{
hash = hash * seed + (*str++);
}
return (hash & 0x7FFFFFFF);
}
};
struct DJBHash
{
// DJB Hash Function
unsigned int operator()(const char* str)
{
unsigned int hash = 5381;
while (*str)
{
hash += (hash << 5) + (*str++);
}
return (hash & 0x7FFFFFFF);
}
};
template<size_t N,class hashFunc1 = DJBHash,class hashFunc2 = BKDRHash,class hashFun3 = SDBMHash>
class BloomFilter
{
private:
typedef BloomFilter<N, hashFunc1, hashFunc2, hashFun3> Self;
const static int M = N * 10;
bitset<M>* _bitset = new bitset<M>;
}
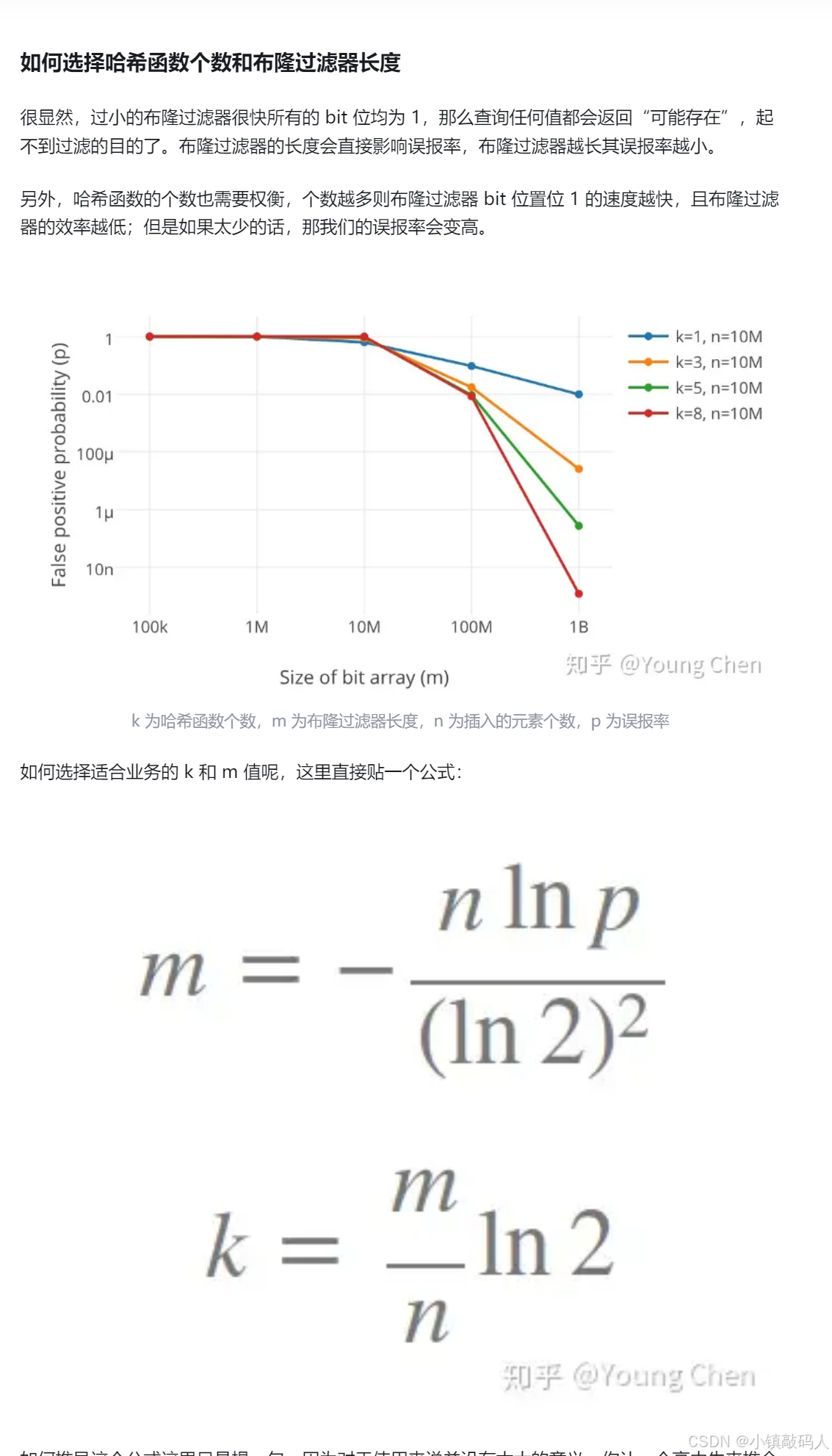
这里M代表布隆过滤器的长度,通常布隆过滤器的长度和要存储的元素的个数有一个对应关系,可以看这篇文章了解
这三个哈希函数,是用来得到每个字符串存储的三个bit位的。
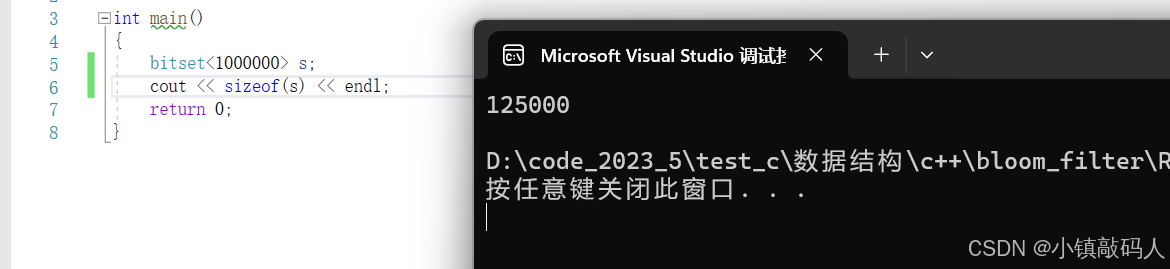
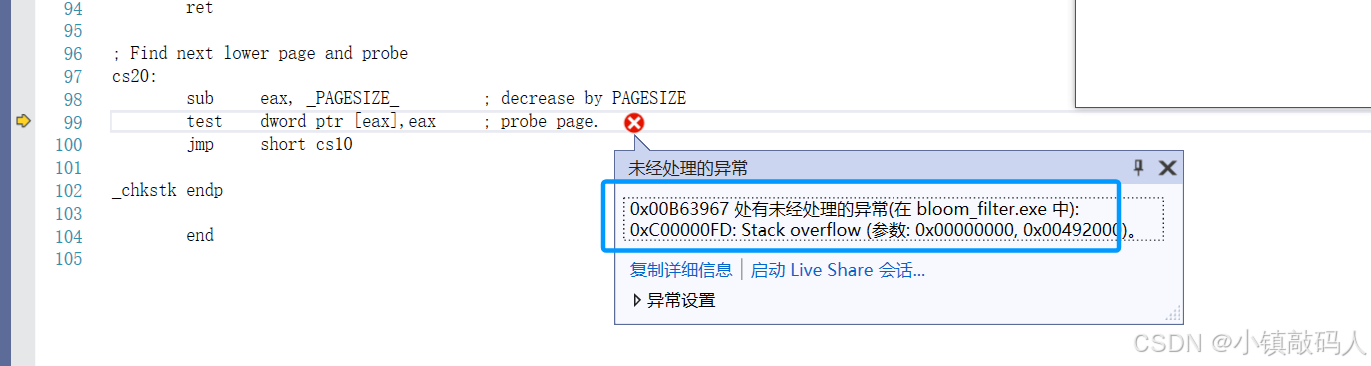
为什么我们要new一个位图对象出来呢,因为库里面的位图是静态变量,空间开在栈上,可能会爆栈。
布隆过滤器的插入
Self& Set(const string& data)
{
hashFunc1 hash1;
hashFunc2 hash2;
hashFun3 hash3;
size_t pos1 = hash1(data.c_str()) % M;
size_t pos2 = hash2(data.c_str()) % M;
size_t pos3 = hash3(data.c_str()) % M;
_bitset->set(pos1);
_bitset->set(pos2);
_bitset->set(pos3);
return *this;
}
布隆过滤器的查找(查找某个元素是否在存在)
bool Test(const string& data)
{
hashFunc1 hash1;
hashFunc2 hash2;
hashFun3 hash3;
size_t pos1 = hash1(data.c_str()) % M;
size_t pos2 = hash2(data.c_str()) % M;
size_t pos3 = hash3(data.c_str()) % M;
if (_bitset.test(pos1) && _bitset.test(pos2) && _bitset.test(pos3))
return true;
return false;
}
只有三个位置同时为1,才代表那个元素是存在的,否则不存在。
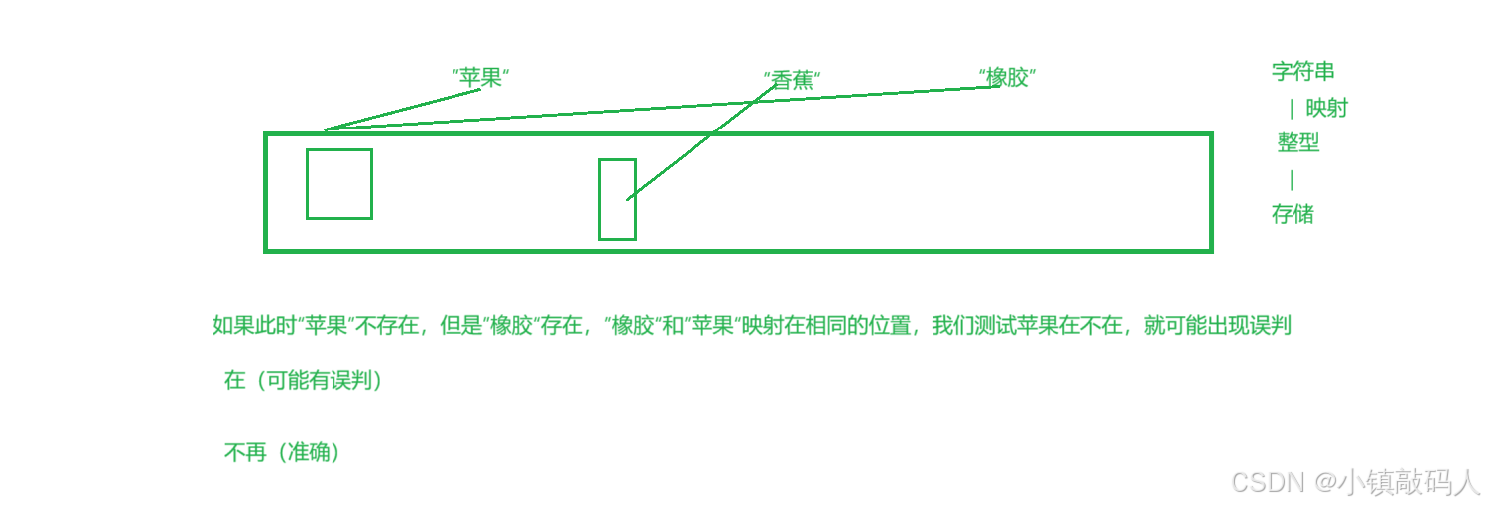
理解布隆过滤器的过滤作用
布隆过滤器的测试
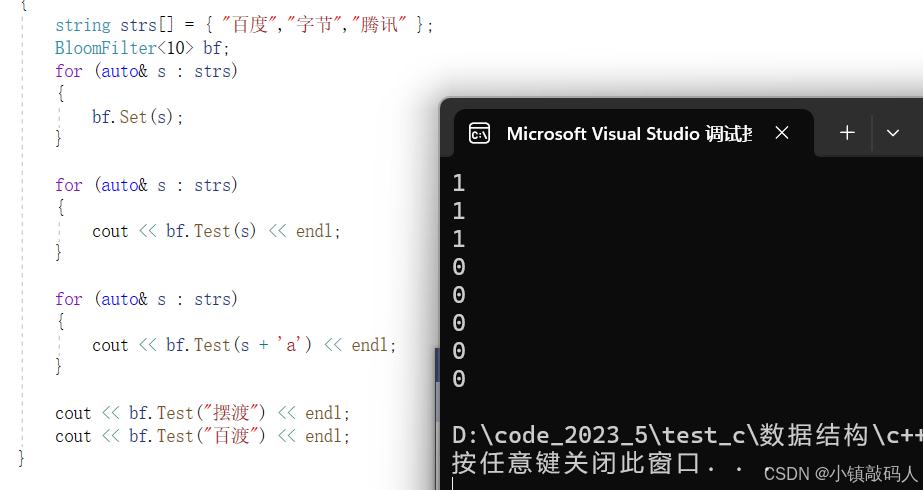
测试1:
void TestBloomFilter1()
{
string strs[] = { "百度","字节","腾讯" };
BloomFilter<10> bf;
for (auto& s : strs)
{
bf.Set(s);
}
for (auto& s : strs)
{
cout << bf.Test(s) << endl;
}
for (auto& s : strs)
{
cout << bf.Test(s + 'a') << endl;
}
cout << bf.Test("摆渡") << endl;
cout << bf.Test("百渡") << endl;
}
运行结果:
测试2:
void TestBloomFilter2()
{
srand(time(0));
const size_t N = 10000000;
BloomFilter<N> bf;
std::vector<std::string> v1;
//std::string url = "https://www.cnblogs.com/-clq/archive/2012/05/31/2528153.html";
//std::string url = "https://www.baidu.com/s?ie=utf-8&f=8&rsv_bp=1&rsv_idx=1&tn=65081411_1_oem_dg&wd=ln2&fenlei=256&rsv_pq=0x8d9962630072789f&rsv_t=ceda1rulSdBxDLjBdX4484KaopD%2BzBFgV1uZn4271RV0PonRFJm0i5xAJ%2FDo&rqlang=en&rsv_enter=1&rsv_dl=ib&rsv_sug3=3&rsv_sug1=2&rsv_sug7=100&rsv_sug2=0&rsv_btype=i&inputT=330&rsv_sug4=2535";
std::string url = "猪八戒";
for (size_t i = 0; i < N; ++i)
{
v1.push_back(url + std::to_string(i));
}
for (auto& str : v1)
{
bf.Set(str);
}
// v2跟v1是相似字符串集(前缀一样),但是后缀不一样
std::vector<std::string> v2;
for (size_t i = 0; i < N; ++i)
{
std::string urlstr = url;
urlstr += std::to_string(N + i);
v2.push_back(urlstr);
}
size_t n2 = 0;
for (auto& str : v2)
{
if (bf.Test(str)) // 误判
{
++n2;
}
}
cout << "相似字符串误判率:" << (double)n2 / (double)N << endl;
// 不相似字符串集 前缀后缀都不一样
std::vector<std::string> v3;
for (size_t i = 0; i < N; ++i)
{
//string url = "zhihu.com";
string url = "孙悟空";
url += std::to_string(N + rand());
v3.push_back(url);
}
size_t n3 = 0;
for (auto& str : v3)
{
if (bf.Test(str))
{
++n3;
}
}
cout << "不相似字符串误判率:" << (double)n3 / (double)N << endl;
}
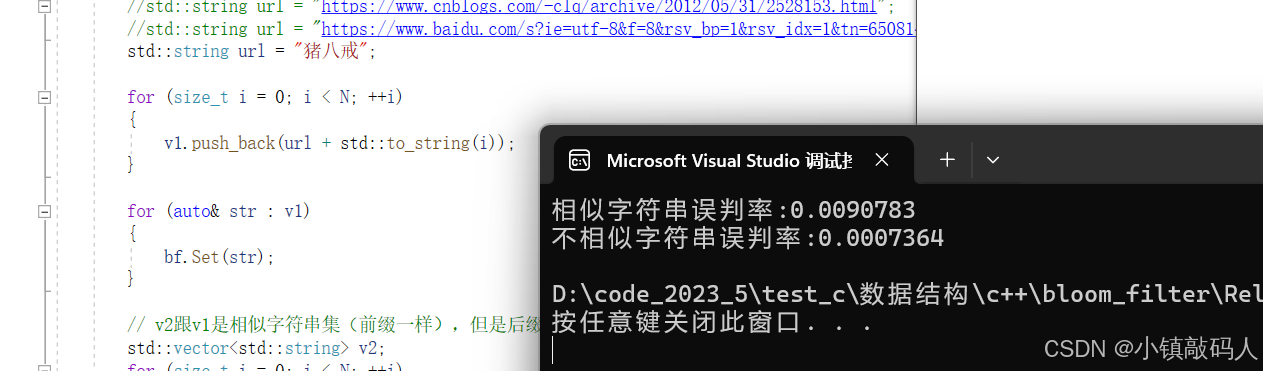
运行结果:
这里可以看到,布隆过滤器是存在误判的,既然存在误判我们就不能支持布隆过滤器的删除,因为你无法确定那个值是否存在,有可能是其它的值映射到了那个地方,即使使用计数法也不行(计数法可解决有其它值的某个位也映射到了相同的位置的问题)。但是计数法提供了参考,如果我们能够精确判断某个值真的在容器中,就可以使用计数法删除。
计数回绕问题:
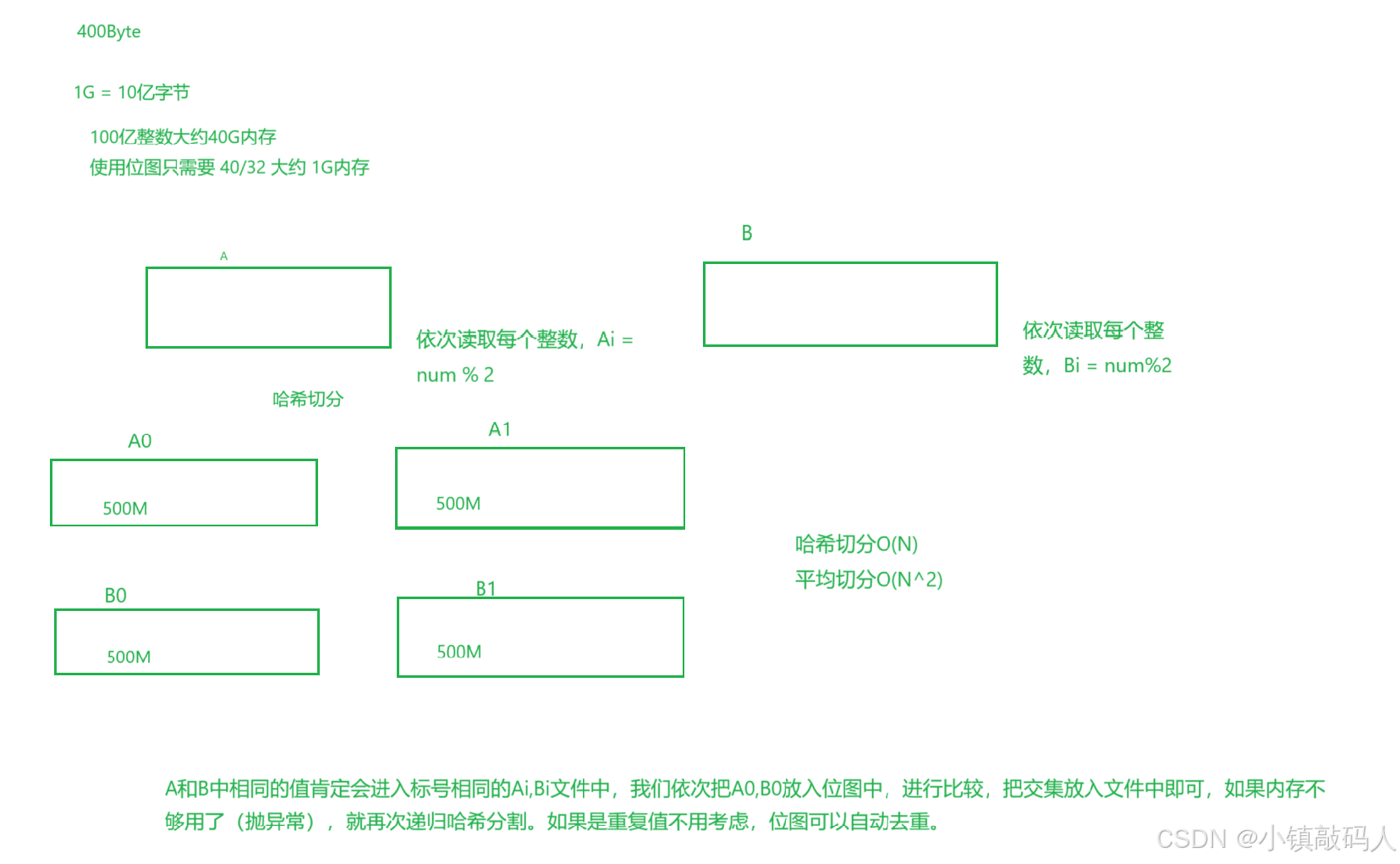
位图的常见面试题
代码简单实现:
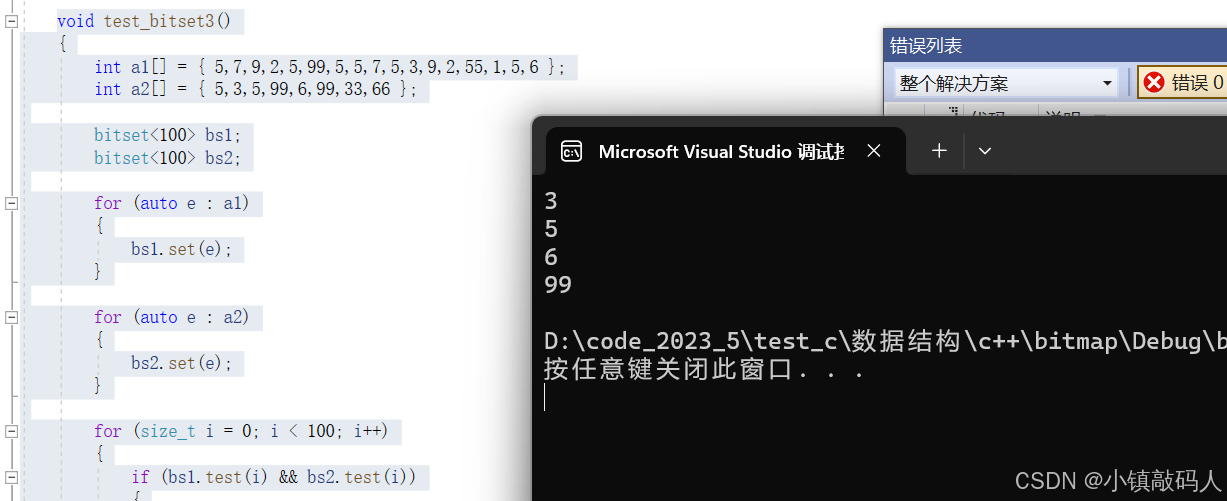
void test_bitset3()
{
int a1[] = { 5,7,9,2,5,99,5,5,7,5,3,9,2,55,1,5,6 };
int a2[] = { 5,3,5,99,6,99,33,66 };
bitset<100> bs1;
bitset<100> bs2;
for (auto e : a1)
{
bs1.set(e);
}
for (auto e : a2)
{
bs2.set(e);
}
for (size_t i = 0; i < 100; i++)
{
if (bs1.test(i) && bs2.test(i))
{
cout << i << endl;
}
}
}
运行结果:
给上面代码加上文件操作就完整的可以模拟上面的问题,这里我们只测试核心的算法部分。
代码实现:
template<size_t N>
class two_bitset
{
private:
bitset<N> _bitset1;//高位
bitset<N> _bitset2;//低位
public:
typedef two_bitset<N> Self;
Self& set(size_t pos)
{
if (_bitset1.test(pos) == false && _bitset2.test(pos) == false)//00
{
//00->01
_bitset2.set(pos);
}
else if (_bitset1.test(pos) == false && _bitset2.test(pos) == true)//01
{
//01->10
_bitset1.set(pos);
}
return *this;
}
bool test(size_t pos)
{
if (_bitset1.test(pos) == false && _bitset2.test(pos))//01
return true;
return false;
}
};
我们只需要处理小于2的次数即可,其余的不用管。
测试代码:
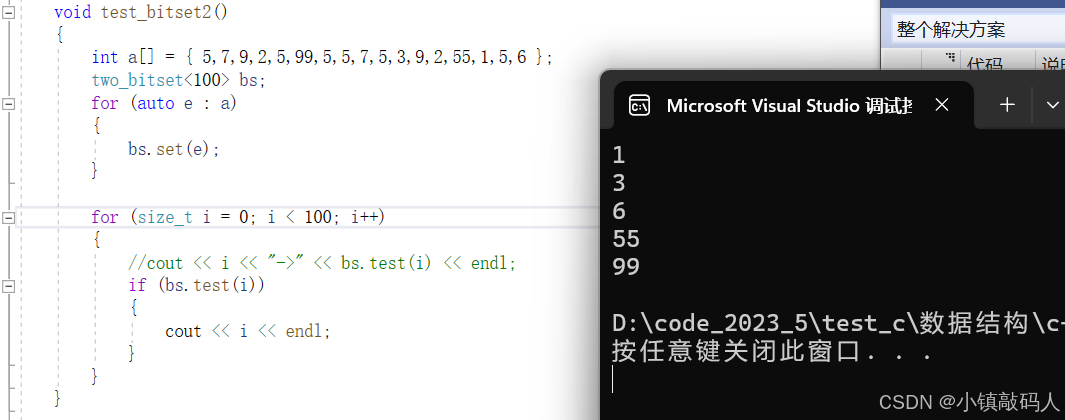
void test_bitset2()
{
int a[] = { 5,7,9,2,5,99,5,5,7,5,3,9,2,55,1,5,6 };
two_bitset<100> bs;
for (auto e : a)
{
bs.set(e);
}
for (size_t i = 0; i < 100; i++)
{
//cout << i << "->" << bs.test(i) << endl;
if (bs.test(i))
{
cout << i << endl;
}
}
}
运行结果:
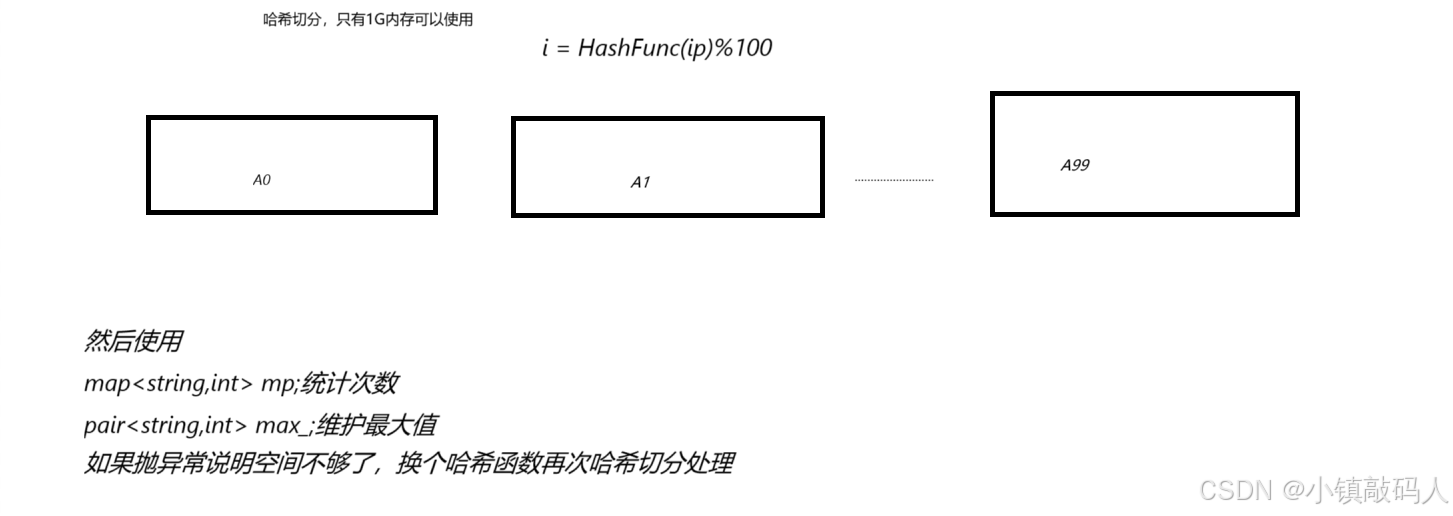
找top K(假设找前K个出现次数最多的IP地址)就创建一个小堆即可。
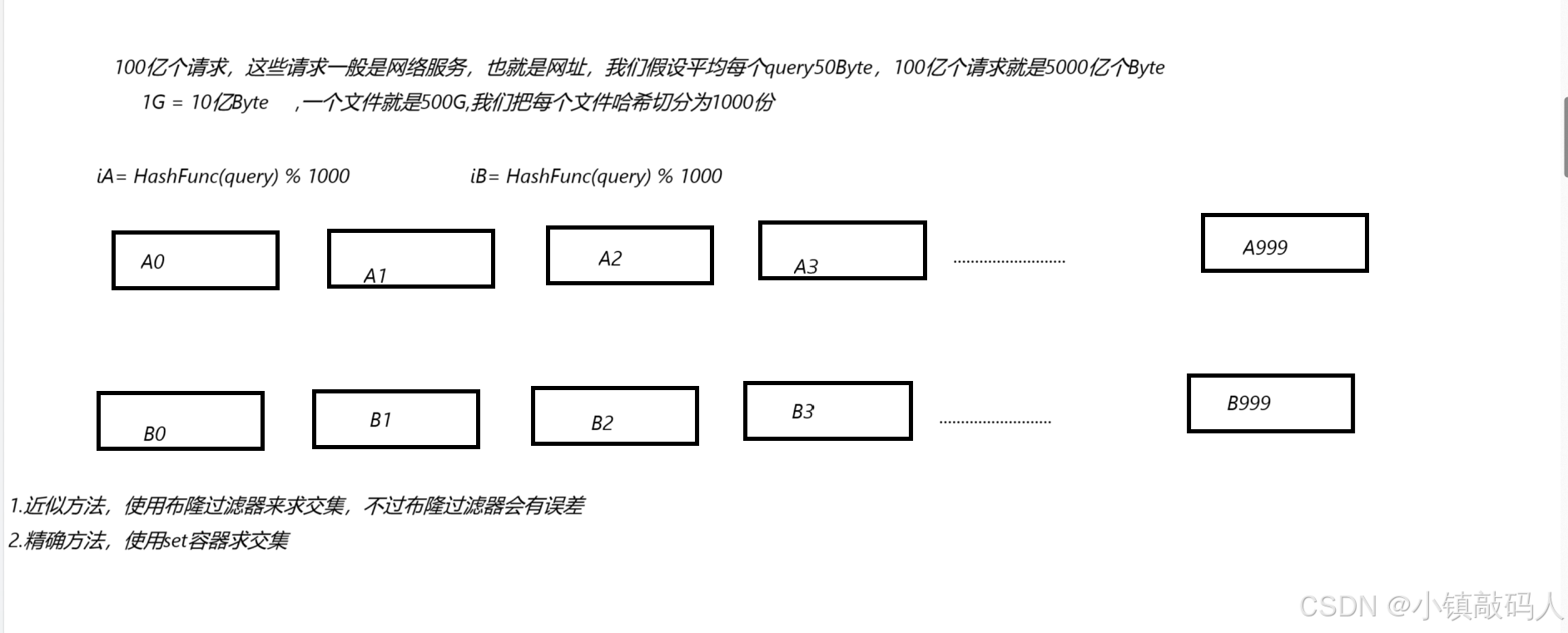
布隆过滤器的常见面试题
总结海量数据处理方法
- 本人知识、能力有限,若有错漏,烦请指正,非常非常感谢!!!
- 转发或者引用需标明来源。