排序算法--计数排序

唯一种没有比较的排序(指没有前后比较,还是有交换的)。统计每个元素出现的次数，直接计算元素在有序序列中的位置，要求数据是整数且范围有限。适用于数据为小范围整数（如年龄、成绩），数据重复率较高时效率更优。可用于小范围整数排序、基数排序的底层排序(作为基数排序的稳定排序子过程)、统计频率分布(快速获取元素分布直方图)、海量数据预处理(配合外部排序处理大数据文件)

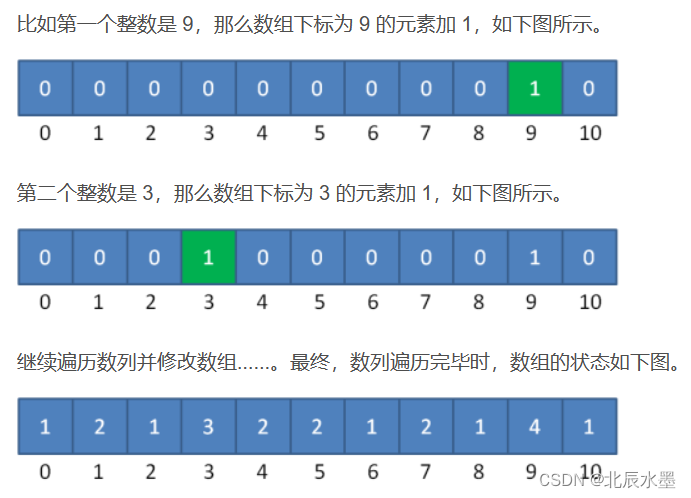
以数组的下标当做数值，有这个数的时候a[i]++;

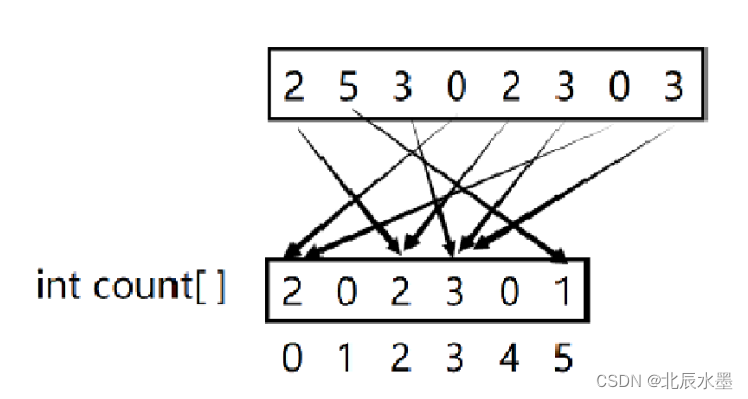
1绝对映射：

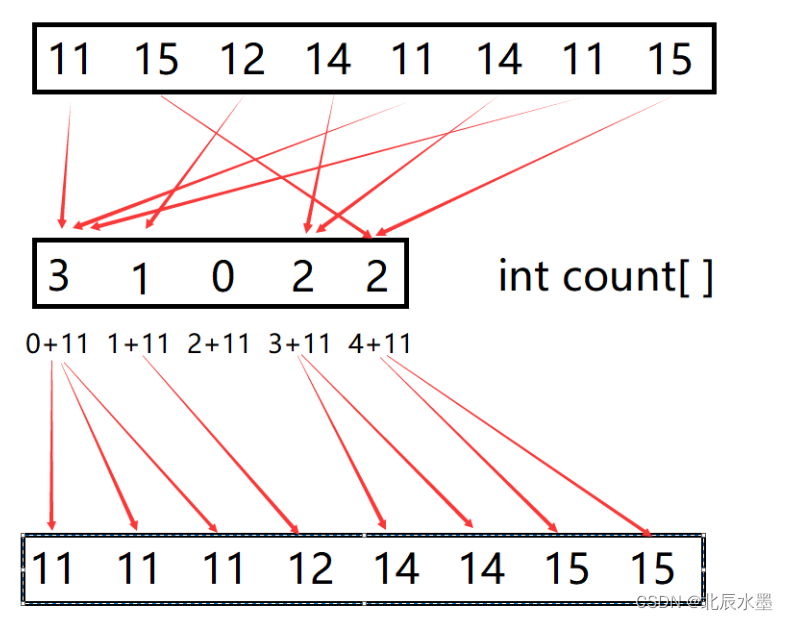
2相对映射：

#include <stdlib.h>
#include <assert.h>

// 计数排序核心函数（稳定排序版本）
void countingSort(int arr[], int n) {
    if (n <= 1) return; // 无需排序

    // 1. 确定数据范围
    int max = arr[0], min = arr[0];
    for (int i = 1; i < n; i++) {
        if (arr[i] > max) max = arr[i];
        if (arr[i] < min) min = arr[i];
    }
    const int range = max - min + 1; // 实际数值范围

    // 2. 创建计数数组并初始化
    int* count = (int*)calloc(range, sizeof(int));
    assert(count != NULL);

    // 3. 统计每个元素出现次数
    for (int i = 0; i < n; i++) {
        count[arr[i] - min]++; // 偏移处理负数
    }

    // 4. 计算累计位置（保证稳定性）
    for (int i = 1; i < range; i++) {
        count[i] += count[i - 1];
    }

    // 5. 反向填充结果数组（关键稳定性操作）
    int* output = (int*)malloc(n * sizeof(int));
    assert(output != NULL);
    
    for (int i = n - 1; i >= 0; i--) {
        output[count[arr[i] - min] - 1] = arr[i];
        count[arr[i] - min]--;
    }

    // 6. 复制回原数组
    for (int i = 0; i < n; i++) {
        arr[i] = output[i];
    }

    // 7. 释放内存
    free(count);
    free(output);
}

#include <stdio.h>
// 打印数组
void printArray(int arr[], int size) {
    for (int i = 0; i < size; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");
}

int main() {
    // 测试数据（包含负数）
    int arr[] = {-5, 2, -3, 4, 1, 2, 8, 5, 3, -1};
    int n = sizeof(arr) / sizeof(arr[0]);

    printf("排序前: ");
    printArray(arr, n);

    countingSort(arr, n);

    printf("排序后: ");
    printArray(arr, n);

    return 0;
}

优化建议：

1.通过min值偏移处理负数，支持全整数范围排序

2.通过反向遍历填充输出数组，保留相同元素的原始顺序，已保证稳定性

3.动态计算range值，避免不必要的内存浪费

void countingSortSpaceOptimized(int arr[], int n) {
    // ...（省略范围计算步骤）...
    
    // 直接根据计数数组覆盖原数组（非稳定）
    int idx = 0;
    for (int i = 0; i < range; i++) {
        while (count[i]-- > 0) {
            arr[idx++] = i + min;
        }
    }
}

排序算法--计数排序

悦读