KNN算法及基于该算法的回归和分类实践

说明

前两天无意间翻到一篇文章：[1]Machine Learning: 十大机器学习算法 - 知乎，里面讲到了十种最基本的机器学习算法，粗略看了一遍，和我最近学习以及实践的内容很契合，文中所罗列的十种机器学习算法中，我目前已经完成了：线性回归[2]、支持向量机[3]、逻辑回归[4]、K-Means[5]四种，后续如果时间和精力允许的话，我打算把剩下的几种算法都尝试一遍。乍一看，剩下的六个算法中，似乎KNN算法是最简单的，本文探讨和实践K最近邻(K-Nearest Neighbors, KNN)算法。

Blog

2024.10.30 博文第一次写作

一、KNN算法概述

KNN算法的概念并不抽象，原理也简单，仅凭文字描述我们其实就能理解这个算法是做什么的，以及如何实现。

KNN算法既可以用来做回归，也可以用来做分类，其核心思想是：

对于回归：我们可以用与某个样本在特征空间中最相邻的K个样本的样本值均值(或加权均值)来预测该样本的样本值。

对于分类：在特征空间中，如果某个样本的K个最相邻的样本中的大多数属于某个类别，那么我们认为该样本也属于这个类别。

对这两段话做拆解(理解)

拆解1，关于最相邻：上面两段描述中，都涉及到最相邻这个词，这就要求我们计算待回归(或分类)样本与其它样本之间的距离。关于距离的计算，我们常用的有：欧式距离和曼哈顿距离。举个例子，假设样本1的特征为：

(1-1)

式中，n为样本特征数。同时，假设样本2的特征为：

(1-2)

那么欧式距离和曼哈顿距离的分别为：

（欧式距离） (1-3)

（曼哈顿距离） (1-4)

在后文的实践中，我将使用欧式距离来计算距离。

需要注意的是：为确保所有特征在计算距离时有相等的权重，我们一般要对样本特征进行预处理：归一化或者标准化。(在后文的实践中，我将直接通过除以各特征最大值的方法来实现归一化，读者也可以做其它的尝试，一般针对不同特性的特征，应该选取适当的归一化方法。)

此外还需要注意的是：为了求得K个最相邻的样本，这要求我们计算待回归(或分类)样本与训练集中所有样本之间的距离，然后再排序，并进而得到K个最相近距离对应的样本。这也体现了KNN算法的缺点：计算复杂度高、空间复杂度高。

拆解2，关于K的值。不难理解的是，和我们熟知的梯度下降法中的学习率一样，K值就是KNN算法里的超参数了，K值的选取会直接影响到回归或分类的效果。一般来说，K值较小时，模型对训练数据的拟合程度较高，但可能容易受到噪声的影响，导致过拟合；K值较大时，模型对训练数据的拟合程度降低，但可能增加模型的泛化能力，减少过拟合的风险。我看一些文章里说，该值一般不建议超过20，且应该随着训练集样本数量的增加而适当增大(不能超过训练集的样本数量)。

关于K值的选择，除了比较直球地多次尝试然后选择一个比较合适的值外。一个推荐的方法是：交叉验证法。所谓交叉验证法，就是把我们的数据集多次划分（为训练集和测试集），然后重复训练和测试，直到得到一个在多种划分下效果都比较好的K值。【不过本文的实践中，我不会尝试该方法，我直接给出一个尝试过几次后还算比较合适的K值。读者可以基于所提供的代码，只需改变训练集和测试集的划分，即可自行实践交叉验证法】

拆解3，关于KNN算法中的训练集和测试集。上面的拆解中聊到了KNN算法下的训练集和测试集。其实从前面对KNN算法核心思想的介绍来看，KNN下并没有所谓的模型、也没有所谓的训练过程！ KNN算法的实现过程就是，从测试集中拿出样本，然后与训练集的所有样本进行比较，随后进行回归或分类的预测处理。

总结：基于KNN算法进行回归和分类的处理流程。

图1.1 基于KNN算法进行回归的处理流程

图1.2 基于KNN算法进行分类的处理流程

在前文的基础上，我们可以实践KNN算法了。为方便与之前的回归/分类文章([2]~[6])的对比。后文的实践中，采用的数据集分别是：UCI的Real Estate数据集[7](用于回归实践)和Iris数据集[8](用于分类实践)。读者可以从参考资料给链接中去网站里下载这两份数据集，同时我也将这两份数据集一并打包在了后文的代码链接中。

二、基于KNN算法的回归实践

2.1 数据集介绍

该Real Estate数据集[7]，一共有414个样本，每个样本有6个特征：交易日期、房屋年龄、离最近交通枢纽的距离、周边商场的数量、房屋的地理维度、地理经度，其样本值为房屋价格。 有关该数据集更细节的说明读者可以移步我之前的博文[2] 4.1节查看。

本章的实践中，随机选择其中2/3的数据作为训练集，剩余1/3的数据作为测试集，来实践KNN算法的回归效果。

2.2 回归实践结果

预设K值为10。得到的结果如下：

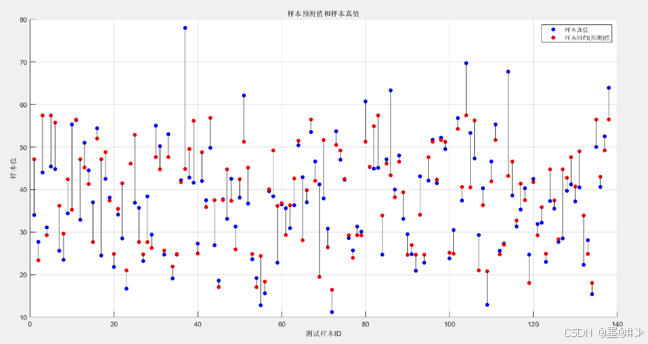
图2.1 测试样本真实值和预测值

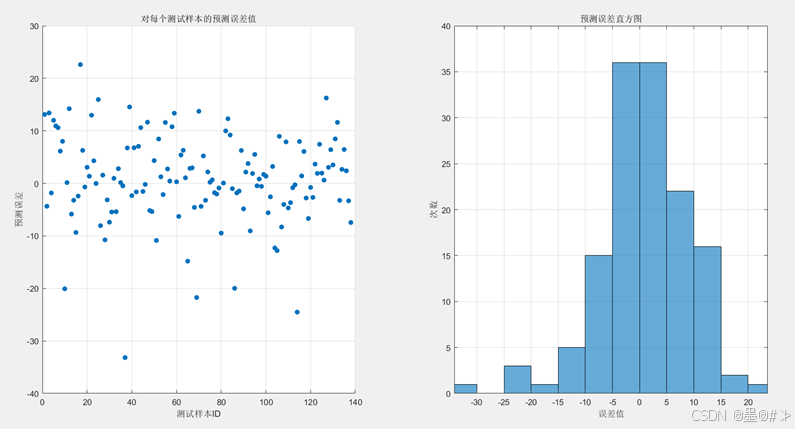
图2.2 测试样本预测误差值&误差直方图

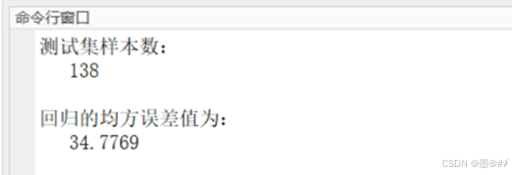
图2.3 测试样本集的均方误差值(多除以了2)

上面所展示的结果其实和我在博文[2]中使用线性模型&梯度下降法求得的结果很接近。结果符合预期。

2.3 本章小结

本章基于KNN算法实践了对数据集[7]的回归，达到了预期的效果，验证了前述理论和所编代码的准确性。读者可以基于本文提供的代码做更深的探讨(比如可以获取不同K值下的均方误差值曲线，从而挑选更合适的K值)。

三、基于KNN算法的分类实践

3.1 数据集介绍

Iris数据集[8]，一共有150个样本，分为三类，每类有50个样本，每个样本有4个特征(花萼长度、花萼宽度、花瓣长度、花瓣宽度)。 有关该数据集更细节的说明读者可以移步我之前的博文[9] 2.1节查看。

本章的实践中，随机选择其中2/3的数据作为训练集，剩余1/3的数据作为测试集，来实践KNN算法的分类效果。

3.2 分类实践结果

预设K值为5，得到的分类结果如下：

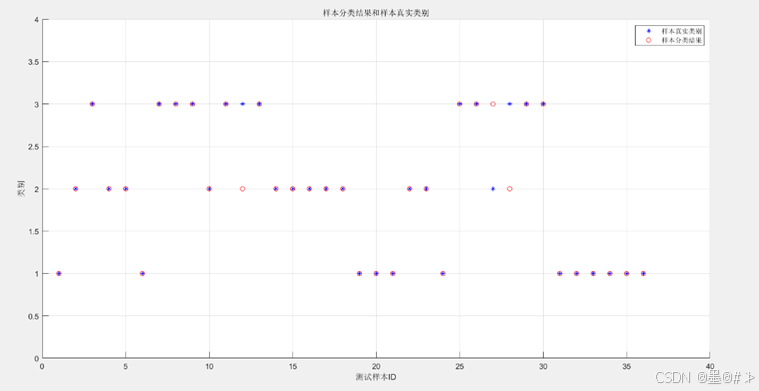
图3.1 测试集分类结果以及与样本真实类别的对比

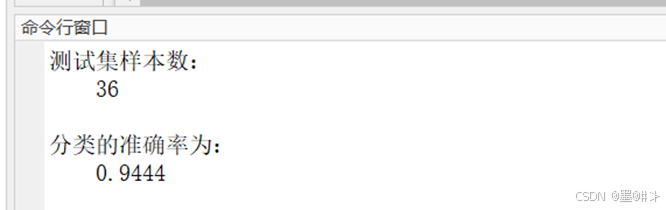
图3.2 测试集分类准确率

准确率还蛮高的，虽然略低于我在博文[4]、[6]中使用逻辑回归和Softmax回归的分类准确率(不过都没有用蒙特卡洛方法进行多次试验)。但KNN算法胜在原理简单、计算简单、编程也简单。

3.3 本章小结

本章基于KNN算法实践了对数据集[8]的分类，达到了预期的效果，验证了前述理论和所编代码的准确性。读者可以基于本文提供的代码做更深的探讨(比如可以获取不同K值下的分类准确率曲线，从而挑选更合适的K值)。

四、总结

本文围绕KNN算法展开，首先对其实现原理和一些实现细节做了论述，随后基于该算法分别进行了回归和分类实践，实践结果都符合预期。KNN算法的优势是：原理简单，实现起来很容易，对特殊值不敏感，可以很方便处理复杂的非线性关系(因为其只关注特征空间内的欧式距离)；不过其缺点也很显著：计算复杂度高、空间复杂度高(特别是训练集的样本数量大、特征数多时)，此外需要选择合适的K值。

本文的工作进一步丰富了专栏：机器学习_墨@#≯的博客-CSDN博客的工具箱！为后续更复杂的深度学习等内容的理解和实践打下了基础。