缘由洛谷P1080 国王游戏 wa一个点_编程语言-CSDN问答

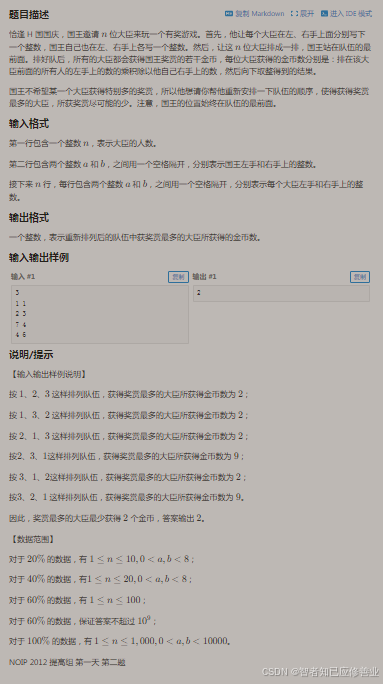
用数据分析推导：左手按升序右手按升序计算即可，由于涉及大数乘法和除法，研究如何变换算法就显得有点意思了，可以把大整数转为整数范围内运算，玩推导就是个乐子，确实是个乐子。
积商不变性质，如：7*5*2/4=3*5*2/4+1*5*2=3*1*2/4+1*5*2+1*2*3=2/4+1*5*2+1*2*3+1=17.5，
7*4*2/7=0*4*2/7+1*2*4=8=1*4*2/1，4*2/4=0*2/4+1*2=2=1*2/1，
7*4*2/4=7*0*2/4+1*7*2=14=3*4*2/4+1*4*2=3*0*2/4+1*4*2+1*2*3=14。
如果看得懂的话，使用以上推导去做，可减小乘积的量，同时使用LONG LONG数据类型的话，对100的数据应该足够使用，免去编写大数运算，其实，已经解题了，且程序也变得更容易实现。

void 洛谷P1080国王游戏()
{
	int a[1080][3]{}, n = 0, j = 0, x = 0;
	bool k = 1; long long m = 0;
	std::cin >> n >> a[0][0] >> a[0][1];
sr:if (x++ < n)
{//3 1 1 2 3 7 4 4 6//4 1 1 2 3 7 4 4 6 7 7
	   std::cin >> a[x][0] >> a[x][1];
	   goto sr;
}
px:if (j < n)
{//左手右手升序
	   if (--x > j)
	   {
		   if (a[x][0] < a[x - 1][0])
			   两数交换(a[x][0], a[x - 1][0]), 两数交换(a[x][1], a[x - 1][1]), k = 0;
		   if (a[x][0] == a[x - 1][0] && a[x][1] < a[x - 1][1])
			   两数交换(a[x][0], a[x - 1][0]), 两数交换(a[x][1], a[x - 1][1]), k = 0;
		   if (x < n)
		   {
			   if (a[n - x][0] > a[n - x + 1][0])
				   两数交换(a[n - x][0], a[n - x + 1][0]), 两数交换(a[n - x][1], a[n - x + 1][1]), k = 0;
			   if (a[n - x][0] == a[n - x + 1][0] && a[n - x][1] > a[n - x + 1][1])
				   两数交换(a[n - x][0], a[n - x + 1][0]), 两数交换(a[n - x][1], a[n - x + 1][1]), k = 0;
		   }
	   }
	   if (x == j)
	   {
		   x = n - j;
		   if (k)j = n;
		   else ++j, k = 1;
	   }
	   goto px;
}
js:if (n)
{
	   if (a[--j][0] >= a[n][1])
	   {
		   a[j][2] = a[j][0] / a[n][1], a[j][0] %= a[n][1];
		   x = n;
	   qs:if (x--){ if (x != j)a[j][2] *= a[x][0]; goto qs; }
	   }
	   else if (a[j][0] < a[n][1])
	   {
		   if (j)a[j - 1][0] *= a[j][0], a[j][0] = 1;
		   else goto sc;
	   }
	   if (a[j][0] == 0)
	   {
	   sc:if (++x < n){ m += a[x][2]; goto sc; }
		   std::cout << m << "\n"; n = 0;
	   }
	   goto js;
}
}



px:if (j < n)
{//左手升序,右手降序
	if (--x > j)
	{
		if (a[x][0] < a[x - 1][0])
			两数交换(a[x][0], a[x - 1][0]), 两数交换(a[x][1], a[x - 1][1]), k = 0;
		if (a[x][0] == a[x - 1][0] && a[x][1] > a[x - 1][1])
			两数交换(a[x][0], a[x - 1][0]), 两数交换(a[x][1], a[x - 1][1]), k = 0;
		if (x < n)
		{
			if (a[n - x][0] > a[n - x + 1][0])
				两数交换(a[n - x][0], a[n - x + 1][0]), 两数交换(a[n - x][1], a[n - x + 1][1]), k = 0;
			if (a[n - x][0] == a[n - x + 1][0] && a[n - x][1] < a[n - x + 1][1])
				两数交换(a[n - x][0], a[n - x + 1][0]), 两数交换(a[n - x][1], a[n - x + 1][1]), k = 0;
		}
	}
	if (x == j)
	{
		x = n - j;
		if (k)j = n;
		else ++j, k = 1;
	}
	goto px;
}

 
可见对二维数组不同升降排序非常简便实现。

商不变性质：积是除数的倍数，a*b/c=c*n/c=n；如果a*b是c的倍数则商是倍数；如：7*4/4=7。
积商不变性质，变为加法运算：7/4=4/4+3/4=1+0.75，2*7/4=2*3/4+1*2=2/4+3=3.5，
2*5*7/4=2*7*（4/4+1/4）/4=1*2*7+2*7*1/4=14+2*（4/4+3/4）=14+2+2*3/4=16+2/4+1=17.5，
（2*5）*7/4=2*7+2*7/4=14+3+2/4=17.5，1*2*7+1*2*7/4=14+3+2/4=17.5，2*1*3/4+（1*2*7+1*2）=16+6/4=16+1+2/4=17.5，3*5*2/4+1*5*2=3*1*2/4+1*5*2+1*2*3=2/4+1*5*2+1*2*3+1=17.5。