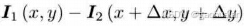视觉里程计-直接法

文章目录

LK光流
直接法

光流：描述像素随时间在图像之间运动的方法。

稀疏光流：计算部分像素运动。以LK（Lucas-Kanade）为代表。
稠密光流：计算所有像素运动。以Horn-Schunck为代表。

直接法：根据像素的亮度信息估计相机运动。

稀疏直接法：P来自稀疏关键点；快速求解相机位姿，适用于实时性较高、计算资源有限的场合。
半稠密直接法：P来自部分像素；
稠密直接法：P为所有像素。适用于建立完整地图。
备注：假设P为空间点，位置已知，深度已知。

直接法优缺点：

优点：
– 省去计算特征点、描述子的时间。
– 只求像素梯度，无需特征点。特征缺失场景下可用。
– 可构建半稠密、稠密地图。
缺点：
– 非凸性。
– 单个像素没有区分度。
– 灰度值不变是很强的假设。

LK光流

OpenCV光流

calcOpticalFlowPyrLK
输入：两张图像，特征点
输出：追踪后的特征点，点的状态、误差
ch8/optical_flow.cpp

// use opencv's flow for validation
    vector<Point2f> pt1, pt2;
    for (auto &kp: kp1) pt1.push_back(kp.pt);
    vector<uchar> status;
    vector<float> error;
    t1 = chrono::steady_clock::now();
    cv::calcOpticalFlowPyrLK(img1, img2, pt1, pt2, status, error);
    t2 = chrono::steady_clock::now();
    time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
    cout << "optical flow by opencv: " << time_used.count() << endl;

高斯牛顿法实现光流

单层光流

通过最小化灰度误差估计最优的像素偏移。

单层光流函数定义
OpticalFlowTracker::caculateOpticalFlow，该函数计算指定范围内特征点的光流。
cv:parallel_for_ 并行调用。并行for循环内部是Intel tbb库实现的。我们只需按接口，讲函数本体定义出来，将std:function对象传递给它。

void OpticalFlowSingleLevel(
    const Mat &img1,
    const Mat &img2,
    const vector<KeyPoint> &kp1,
    vector<KeyPoint> &kp2,
    vector<bool> &success,
    bool inverse, bool has_initial) {
    kp2.resize(kp1.size());
    success.resize(kp1.size());
    OpticalFlowTracker tracker(img1, img2, kp1, kp2, success, inverse, has_initial);
    parallel_for_(Range(0, kp1.size()),
                  std::bind(&OpticalFlowTracker::calculateOpticalFlow, &tracker, placeholders::_1));
}

计算光流

void OpticalFlowTracker::calculateOpticalFlow(const Range &range) {
    // parameters
    int half_patch_size = 4;
    int iterations = 10;
    for (size_t i = range.start; i < range.end; i++) {
        auto kp = kp1[i];
        double dx = 0, dy = 0; // dx,dy need to be estimated
        if (has_initial) {
            dx = kp2[i].pt.x - kp.pt.x;
            dy = kp2[i].pt.y - kp.pt.y;
        }

        double cost = 0, lastCost = 0;
        bool succ = true; // indicate if this point succeeded

        // Gauss-Newton iterations
        Eigen::Matrix2d H = Eigen::Matrix2d::Zero();    // hessian
        Eigen::Vector2d b = Eigen::Vector2d::Zero();    // bias
        Eigen::Vector2d J;  // jacobian
        for (int iter = 0; iter < iterations; iter++) {
            if (inverse == false) {
                H = Eigen::Matrix2d::Zero();
                b = Eigen::Vector2d::Zero();
            } else {
                // only reset b
                b = Eigen::Vector2d::Zero();
            }

            cost = 0;

            // compute cost and jacobian
            for (int x = -half_patch_size; x < half_patch_size; x++)
                for (int y = -half_patch_size; y < half_patch_size; y++) {

计算残差,残差公式
在这里插入图片描述

                    double error = GetPixelValue(img1, kp.pt.x + x, kp.pt.y + y) -
                                   GetPixelValue(img2, kp.pt.x + x + dx, kp.pt.y + y + dy);;

计算雅可比矩阵

// Jacobian
                    if (inverse == false) {
                        J = -1.0 * Eigen::Vector2d(
                            0.5 * (GetPixelValue(img2, kp.pt.x + dx + x + 1, kp.pt.y + dy + y) -
                                   GetPixelValue(img2, kp.pt.x + dx + x - 1, kp.pt.y + dy + y)),
                            0.5 * (GetPixelValue(img2, kp.pt.x + dx + x, kp.pt.y + dy + y + 1) -
                                   GetPixelValue(img2, kp.pt.x + dx + x, kp.pt.y + dy + y - 1))
                        );
                    } else if (iter == 0) {
                        // in inverse mode, J keeps same for all iterations
                        // NOTE this J does not change when dx, dy is updated, so we can store it and only compute error
                        J = -1.0 * Eigen::Vector2d(
                            0.5 * (GetPixelValue(img1, kp.pt.x + x + 1, kp.pt.y + y) -
                                   GetPixelValue(img1, kp.pt.x + x - 1, kp.pt.y + y)),
                            0.5 * (GetPixelValue(img1, kp.pt.x + x, kp.pt.y + y + 1) -
                                   GetPixelValue(img1, kp.pt.x + x, kp.pt.y + y - 1))
                        );
                    }
                    // compute H, b and set cost;
                    b += -error * J;
                    cost += error * error;
                    if (inverse == false || iter == 0) {
                        // also update H
                        H += J * J.transpose();
                    }
                }

            // compute update
            Eigen::Vector2d update = H.ldlt().solve(b);

            if (std::isnan(update[0])) {
                // sometimes occurred when we have a black or white patch and H is irreversible
                cout << "update is nan" << endl;
                succ = false;
                break;
            }

            if (iter > 0 && cost > lastCost) {
                break;
            }

            // update dx, dy
            dx += update[0];
            dy += update[1];
            lastCost = cost;
            succ = true;

            if (update.norm() < 1e-2) {
                // converge
                break;
            }
        }

        success[i] = succ;

        // set kp2
        kp2[i].pt = kp.pt + Point2f(dx, dy);
    }
}

多层光流

引入图像金字塔，解决相机运动过快时，单层光流效果不佳的问题（容易达到局部极小值）。
图像金字塔，是对同一个图像进行缩放，得到不同分辨率的图像。

void OpticalFlowMultiLevel(
    const Mat &img1,
    const Mat &img2,
    const vector<KeyPoint> &kp1,
    vector<KeyPoint> &kp2,
    vector<bool> &success,
    bool inverse) {

    // parameters
    int pyramids = 4;
    double pyramid_scale = 0.5;
    double scales[] = {1.0, 0.5, 0.25, 0.125};

    // create pyramids
    chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
    vector<Mat> pyr1, pyr2; // image pyramids
    for (int i = 0; i < pyramids; i++) {
        if (i == 0) {
            pyr1.push_back(img1);
            pyr2.push_back(img2);
        } else {
            Mat img1_pyr, img2_pyr;
            cv::resize(pyr1[i - 1], img1_pyr,
                       cv::Size(pyr1[i - 1].cols * pyramid_scale, pyr1[i - 1].rows * pyramid_scale));
            cv::resize(pyr2[i - 1], img2_pyr,
                       cv::Size(pyr2[i - 1].cols * pyramid_scale, pyr2[i - 1].rows * pyramid_scale));
            pyr1.push_back(img1_pyr);
            pyr2.push_back(img2_pyr);
        }
    }
    chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
    auto time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
    cout << "build pyramid time: " << time_used.count() << endl;

    // coarse-to-fine LK tracking in pyramids
    vector<KeyPoint> kp1_pyr, kp2_pyr;
    for (auto &kp:kp1) {
        auto kp_top = kp;
        kp_top.pt *= scales[pyramids - 1];
        kp1_pyr.push_back(kp_top);
        kp2_pyr.push_back(kp_top);
    }
//从顶层图像开始计算，将上一层的追踪结果，作为下一层光流的初始值。
    for (int level = pyramids - 1; level >= 0; level--) {
        // from coarse to fine
        success.clear();
        t1 = chrono::steady_clock::now();
        OpticalFlowSingleLevel(pyr1[level], pyr2[level], kp1_pyr, kp2_pyr, success, inverse, true);
        t2 = chrono::steady_clock::now();
        auto time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
        cout << "track pyr " << level << " cost time: " << time_used.count() << endl;

        if (level > 0) {
            for (auto &kp: kp1_pyr)
                kp.pt /= pyramid_scale;
            for (auto &kp: kp2_pyr)
                kp.pt /= pyramid_scale;
        }
    }

    for (auto &kp: kp2_pyr)
        kp2.push_back(kp);
}

直接法

ch8/direct_method.cpp

单层直接法

计算雅可比矩阵

定义求雅可比的类

/// class for accumulator jacobians in parallel
class JacobianAccumulator {
public:
    JacobianAccumulator(
        const cv::Mat &img1_,
        const cv::Mat &img2_,
        const VecVector2d &px_ref_,
        const vector<double> depth_ref_,
        Sophus::SE3d &T21_) :
        img1(img1_), img2(img2_), px_ref(px_ref_), depth_ref(depth_ref_), T21(T21_) {
        projection = VecVector2d(px_ref.size(), Eigen::Vector2d(0, 0));
    }

    /// accumulate jacobians in a range
    void accumulate_jacobian(const cv::Range &range);

    /// get hessian matrix
    Matrix6d hessian() const { return H; }

    /// get bias
    Vector6d bias() const { return b; }

    /// get total cost
    double cost_func() const { return cost; }

    /// get projected points
    VecVector2d projected_points() const { return projection; }

    /// reset h, b, cost to zero
    void reset() {
        H = Matrix6d::Zero();
        b = Vector6d::Zero();
        cost = 0;
    }

private:
    const cv::Mat &img1;
    const cv::Mat &img2;
    const VecVector2d &px_ref;
    const vector<double> depth_ref;
    Sophus::SE3d &T21;
    VecVector2d projection; // projected points

    std::mutex hessian_mutex;
    Matrix6d H = Matrix6d::Zero();
    Vector6d b = Vector6d::Zero();
    double cost = 0;
};

求解雅可比矩阵

void JacobianAccumulator::accumulate_jacobian(const cv::Range &range) {

    // parameters
    const int half_patch_size = 1;
    int cnt_good = 0;
    Matrix6d hessian = Matrix6d::Zero();
    Vector6d bias = Vector6d::Zero();
    double cost_tmp = 0;

    for (size_t i = range.start; i < range.end; i++) {

        // compute the projection in the second image
        Eigen::Vector3d point_ref =
            depth_ref[i] * Eigen::Vector3d((px_ref[i][0] - cx) / fx, (px_ref[i][1] - cy) / fy, 1);
        Eigen::Vector3d point_cur = T21 * point_ref;
        if (point_cur[2] < 0)   // depth invalid
            continue;

        float u = fx * point_cur[0] / point_cur[2] + cx, v = fy * point_cur[1] / point_cur[2] + cy;
        if (u < half_patch_size || u > img2.cols - half_patch_size || v < half_patch_size ||
            v > img2.rows - half_patch_size)
            continue;

        projection[i] = Eigen::Vector2d(u, v);
        double X = point_cur[0], Y = point_cur[1], Z = point_cur[2],
            Z2 = Z * Z, Z_inv = 1.0 / Z, Z2_inv = Z_inv * Z_inv;
        cnt_good++;

        // and compute error and jacobian
        for (int x = -half_patch_size; x <= half_patch_size; x++)
            for (int y = -half_patch_size; y <= half_patch_size; y++) {

                double error = GetPixelValue(img1, px_ref[i][0] + x, px_ref[i][1] + y) -
                               GetPixelValue(img2, u + x, v + y);
                Matrix26d J_pixel_xi;
                Eigen::Vector2d J_img_pixel;

                J_pixel_xi(0, 0) = fx * Z_inv;
                J_pixel_xi(0, 1) = 0;
                J_pixel_xi(0, 2) = -fx * X * Z2_inv;
                J_pixel_xi(0, 3) = -fx * X * Y * Z2_inv;
                J_pixel_xi(0, 4) = fx + fx * X * X * Z2_inv;
                J_pixel_xi(0, 5) = -fx * Y * Z_inv;

                J_pixel_xi(1, 0) = 0;
                J_pixel_xi(1, 1) = fy * Z_inv;
                J_pixel_xi(1, 2) = -fy * Y * Z2_inv;
                J_pixel_xi(1, 3) = -fy - fy * Y * Y * Z2_inv;
                J_pixel_xi(1, 4) = fy * X * Y * Z2_inv;
                J_pixel_xi(1, 5) = fy * X * Z_inv;

                J_img_pixel = Eigen::Vector2d(
                    0.5 * (GetPixelValue(img2, u + 1 + x, v + y) - GetPixelValue(img2, u - 1 + x, v + y)),
                    0.5 * (GetPixelValue(img2, u + x, v + 1 + y) - GetPixelValue(img2, u + x, v - 1 + y))
                );

                // total jacobian
                Vector6d J = -1.0 * (J_img_pixel.transpose() * J_pixel_xi).transpose();

                hessian += J * J.transpose();
                bias += -error * J;
                cost_tmp += error * error;
            }
    }

    if (cnt_good) {
        // set hessian, bias and cost
        unique_lock<mutex> lck(hessian_mutex);
        H += hessian;
        b += bias;
        cost += cost_tmp / cnt_good;
    }
}

位姿更新

void DirectPoseEstimationSingleLayer(
    const cv::Mat &img1,
    const cv::Mat &img2,
    const VecVector2d &px_ref,
    const vector<double> depth_ref,
    Sophus::SE3d &T21) {

    const int iterations = 10;
    double cost = 0, lastCost = 0;
    auto t1 = chrono::steady_clock::now();
    JacobianAccumulator jaco_accu(img1, img2, px_ref, depth_ref, T21);

    for (int iter = 0; iter < iterations; iter++) {
        jaco_accu.reset();
        cv::parallel_for_(cv::Range(0, px_ref.size()),
                          std::bind(&JacobianAccumulator::accumulate_jacobian, &jaco_accu, std::placeholders::_1));
        Matrix6d H = jaco_accu.hessian();
        Vector6d b = jaco_accu.bias();

        // solve update and put it into estimation
        Vector6d update = H.ldlt().solve(b);;
        T21 = Sophus::SE3d::exp(update) * T21;
        cost = jaco_accu.cost_func();

        if (std::isnan(update[0])) {
            // sometimes occurred when we have a black or white patch and H is irreversible
            cout << "update is nan" << endl;
            break;
        }
        if (iter > 0 && cost > lastCost) {
            cout << "cost increased: " << cost << ", " << lastCost << endl;
            break;
        }
        if (update.norm() < 1e-3) {
            // converge
            break;
        }

        lastCost = cost;
        cout << "iteration: " << iter << ", cost: " << cost << endl;
    }

    cout << "T21 = \n" << T21.matrix() << endl;
    auto t2 = chrono::steady_clock::now();
    auto time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
    cout << "direct method for single layer: " << time_used.count() << endl;

    // plot the projected pixels here
    cv::Mat img2_show;
    cv::cvtColor(img2, img2_show, CV_GRAY2BGR);
    VecVector2d projection = jaco_accu.projected_points();
    for (size_t i = 0; i < px_ref.size(); ++i) {
        auto p_ref = px_ref[i];
        auto p_cur = projection[i];
        if (p_cur[0] > 0 && p_cur[1] > 0) {
            cv::circle(img2_show, cv::Point2f(p_cur[0], p_cur[1]), 2, cv::Scalar(0, 250, 0), 2);
            cv::line(img2_show, cv::Point2f(p_ref[0], p_ref[1]), cv::Point2f(p_cur[0], p_cur[1]),
                     cv::Scalar(0, 250, 0));
        }
    }
    cv::imshow("current", img2_show);
    cv::waitKey();
}

多层直接法

void DirectPoseEstimationMultiLayer(
    const cv::Mat &img1,
    const cv::Mat &img2,
    const VecVector2d &px_ref,
    const vector<double> depth_ref,
    Sophus::SE3d &T21) {

    // parameters
    int pyramids = 4;
    double pyramid_scale = 0.5;
    double scales[] = {1.0, 0.5, 0.25, 0.125};

    // create pyramids
    vector<cv::Mat> pyr1, pyr2; // image pyramids
    for (int i = 0; i < pyramids; i++) {
        if (i == 0) {
            pyr1.push_back(img1);
            pyr2.push_back(img2);
        } else {
            cv::Mat img1_pyr, img2_pyr;
            cv::resize(pyr1[i - 1], img1_pyr,
                       cv::Size(pyr1[i - 1].cols * pyramid_scale, pyr1[i - 1].rows * pyramid_scale));
            cv::resize(pyr2[i - 1], img2_pyr,
                       cv::Size(pyr2[i - 1].cols * pyramid_scale, pyr2[i - 1].rows * pyramid_scale));
            pyr1.push_back(img1_pyr);
            pyr2.push_back(img2_pyr);
        }
    }

    double fxG = fx, fyG = fy, cxG = cx, cyG = cy;  // backup the old values
    for (int level = pyramids - 1; level >= 0; level--) {
        VecVector2d px_ref_pyr; // set the keypoints in this pyramid level
        for (auto &px: px_ref) {
            px_ref_pyr.push_back(scales[level] * px);
        }

        // scale fx, fy, cx, cy in different pyramid levels
        fx = fxG * scales[level];
        fy = fyG * scales[level];
        cx = cxG * scales[level];
        cy = cyG * scales[level];
        DirectPoseEstimationSingleLayer(pyr1[level], pyr2[level], px_ref_pyr, depth_ref, T21);
    }

}

参考资料：
1、书籍：《视觉SLAM十四讲：从理论到实践（第2版）》
2、代码：https://github.com/gaoxiang12/slambook2